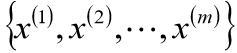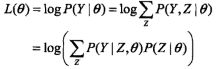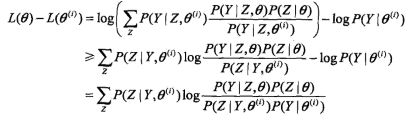EM算法---基于隐变量的参数估计

注：本文中所有公式和思路来自于李航博士的《统计学习方法》一书，我只是为了加深记忆和理解写的本文。】

EM算法算是机器学习中有些难度的算法之一，也是非常重要的算法，曾经被誉为10大数据挖掘算法之一，从标题可以看出，EM专治带有隐变量的参数估计，我们熟悉的MLE(最大似然估计)一般会用于不含有隐变量的参数估计，应用场景不同。

首先举一个带有隐变量的例子吧，假设现在有1000人的身高数据，163、153、183、203、173等等，不出意外肯定是男生或者女生组成的这1000个人，那么这个163cm我们就没办法知道是男生的还是女生，这其中男女就是一个隐变量，我们只能看到163cm，但是看不到背后男女这个隐变量。

用Y表示观测数据，Z表示隐变量（男女身高例子中就是男女这个隐变量），Y和Z在一起表示为完全数据，假设Y、Z的联合分布概率为P(Y,Z|θ)，对数似然为logP(Y,Z|θ)，EM算法通过迭代求得L(θ)=logP(Y,Z|θ)的最大似然估计，每次迭代分为两步：E-step ，求期望。M-step，求最大化，下面来介绍EM算法。

EM算法的提出

假定有训练集：

现在有m个独立样本。希望从中找到该组数据的模型p(x, z)的参数，

我们可以通过最大似然估计建立目标函数，然后取对数似然：

事实上，EM算法是通过迭代逐步接近最大化L(θ)，那么我们现在不妨假设第i次迭代后θ的估计值为θi，我们当然希望重新估计的θ能使似然函数L(θ)有所增大，并逐渐逼近最大值，因此，我们做差：

利用jensen不等式，我们找到其下界：

虽然看上去有点乱，其实就是在里边偷偷的再里边乘上一个P和除上一个P，没任何难度，

令：

则：

由此可知B为L的一个下界，那么我们根据上式可得：

那么任何能使B增加的的θ一定也可以使L(θ)增大，为了使L(θ)尽可能的增大，我们可以选择一个θi+1使得B达到最大：

既然是求θi+1，那么就省略掉常数项：

这就完成了EM算法的一次迭代，EM算法其实就是通过不断求解下界的极大化逼近求解岁数似然函数的极大值算法。

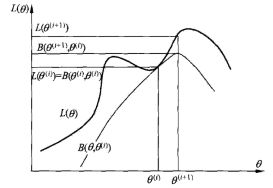
下图使一个比较直观表示EM算法求解过程:

从这幅图中不难看出，EM算法不能保证找到全局最最优值。

算法：

输入：观测数据Y，隐变量Z，联合分布P(Y,Z|θ)，条件分布P(Z|Y,θ)；

输出：模型的参数；

(1): 选择参数的初始值θ0，开始迭代；

(2): E步：记θi为第i次迭代的参数θ的估值，在第θ+1次的迭代，计算：

其中P(Z|Y,θi)是给定观测数据Y和当前参数估计θi的前提下，隐变量Z的条件概率分布。

(3): M步：求使Q(θ，θi)极大值的θ，确定第i+1次的参数估计值θi：

(4): 重复第2、3步，直到收敛。

说明：

完全数据的对数似然函数logP(Y,Z|θ)关于在给定Y和θi的前提下对未观测数据Z的条件概率分布P(Z|Y,θi)的期望称为Q函数：

关于EM算法的几点注意：

步骤(1): θ参数初值是可以随便给定的，但是EM算法对于初值选择是敏感的。

步骤(2): E-step求得Q(θ，θi)，Q函数中Z是隐变量，Y是观测数据，Q(θ，θi)中第一个变元是表示要极大化的参数，第二个表示当前的估计值，每次迭代实际上是在求Q的最大化。

步骤(3): M-step中试求Q(θ，θi)的最大值，得到θi，完成一次迭代。

步骤(4): 给出迭代终止条件，一般是较小的正数ε1，ε2，若满足：

EM算法的过程就介绍到这里，更细致的推导这里就不再介绍了，欢迎批评指正。