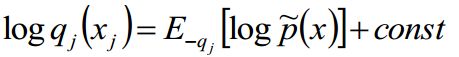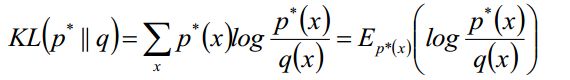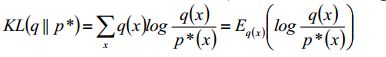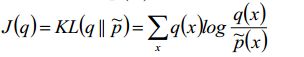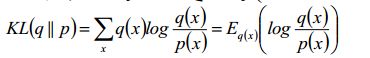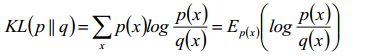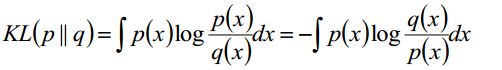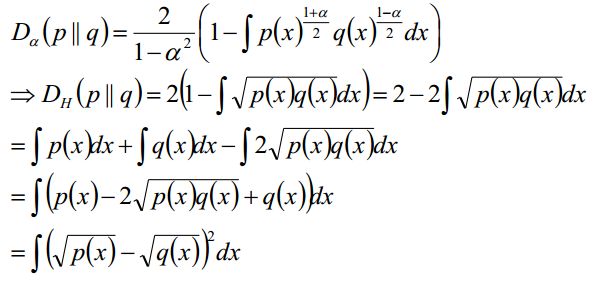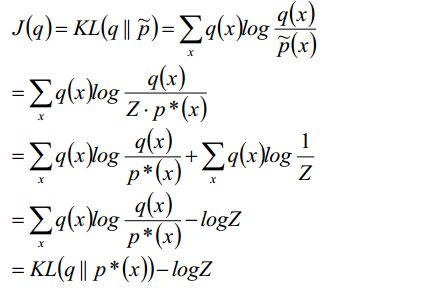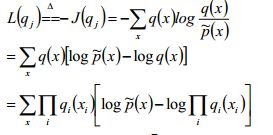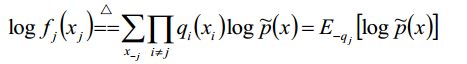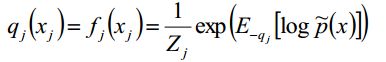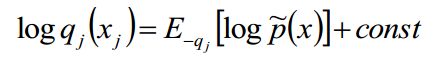变分算法

注：本文中所有公式和思路来自于邹博先生的《机器学习升级版》，我只是为了加深记忆和理解写的本文。

本文介绍的变分算法是机器学习中的参数估计算法，跟数学中的变分法是有一些不一样的。在搜索引擎中搜索变分算法一般都是数学中的变分法，机器学习的好像还真的很少。

变分算法我觉得是机器学习算法中比较难的一个了，因为推导有很多，并且有一些想法是不太直观上被轻易接受或者说理解的，今天斗胆说一说。

我们不妨先看看变分的核心公式：

看起来怪怪的，又是log又是const又是非q的

我们可以先粗略的解释一下这个公式：当我们更新qj的时候，只需要计算和qj有公共边的那些变量即可，也就是j的马尔科夫毯包含的那些点。

看到非q这个东西是不是感觉像Gibbs采样啊，没错，确实是有些相同地方的，那么区别在哪呢：

Gibbs时采用的邻居节点的（相同文档中的词）的主题采样，而变分使用的是相邻结点的期望，很明显这样的话变分的速度是要比采样更快，因为求得是期望嘛，代替了很多次的采样。

我们以前可以用采样的方式改造EM算法，其实就是在E-Step计算条件概率上做点事情：

从上边公式可以看得出，假定p(x)是个不好计算的分布，那么我们可以通过采样的方式来近似，这种算法又叫做MC-EM，展开来还有随机EM等，就不细说了

那么现在我们是不是可以用变分的当时改造EM算法呢？

其实是可以的，我们后边介绍如何改造这里先卖一个关子。

说变分之前，我先说一个概念近似估计：假如现在有一个分布是不容易计算的p(x|D)，那么可以选择一个简单的分布q(x)来近似分布p(x|D)。

这种近似通常都会在精度和速度上折中，那么怎么度量这个近似呢？

变分提出：假定p*(x)是一个(真实)难解的分布，q(x)是一个近似的(容易)的分布-例如多元的高斯分布或者多个简单分布的乘积

如果这个q(x)有n个参数来控制，那么现在的问题就变成了：优化这些参数从而近似(逼近)p*(x)

那么怎么度量p*(x)和q(x)呢，显然我们可以使用KL散度啊：

现在我们来看看这个目标函数，既然我们前面假设p*(x)是一个难解的分布，我们现在目标函数Σ右边竟然还有p*(x)，那目标函数岂不是依然难解，自己打脸呀。

如果用逆KL散度呢？

这样就转换为计算q(x)的期望了，是不是就简单了很多了。

进一步我们再来分析这个难搞的p*(x)：

其中p(D)就是数据发生的似然概率，是一个已知可求的量，可以作为归一化因子，那么接下来整理一下：

这样我们就得到了新的目标函数，其实这样做还有一个好处，就是可以得到局部最小值。为啥呢？

两种KL散度的区别

KL(q||p)，又称为I-投影，信息投影(information projection)

现在仔细看这个公式，p(x)是真实的分布，那么如果p(x)=0是不是KL散度就会无穷大？所以当p(x)=0时候q(x)也必须要为0，也就是该公式对待q(x)是0强制的，所以p(x)往往是被低估的

KL(p||q)，又称为M-投影，矩投影(monent projection)

再仔细看看公式，p(x)是真实的分布，如果p(x)≠0，那么q(x)=0的话，KL散度就会无穷大，所以如果p(x)≠0，那么也只能q(x)≠0，也就是该公式对待q(x)是0避免的，所以p(x)往往是被高估的。

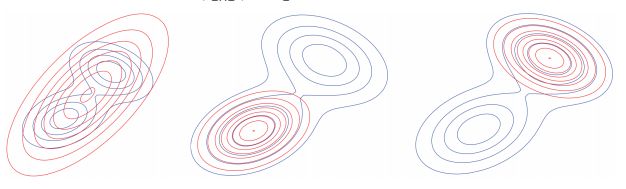
下图种蓝色的线是真实的分布，红色的是两种KL散度的近似效果，其中左边的是KL(p||q)，也就是M投影，可以看得出其实没办法锁住一个峰(也就是没办法求极值)，中间和右边的是KL(q||p)的I投影，因为初始值不同所以锁住的峰是不同的，但是都是可以求出一个极值的，所以我们使用I投影来做目标函数。

其实这个事情还可以说的更清楚，只不过书面上还真是不太容易说的太清楚，也没办法自己边画图边讲，所以尽量说的明白一点。

其实这两种KL散度也是有联系的，q(x)和p(x)也并不是很割裂的，是有关联公式：

首先给出q(x)和p(x)的距离定义：

再给出KL散度：

变换一下其实可以得出以下结论的：

当α=1的时候退化为KL(p||q)

当α=-1的时候退化为KL(q||p)

当α=0的时候就是Hellinger distance：

Hellinger distance是满足三角不等式、对称的，不是本次分享的重点，了解一下就行了。

上面嘚吧嘚吧一大坨其实就是说了两种KL散度的区别，那么新的目标函数就是使用I投影的，我们可以做一下简单的变换：

这个结果就是简单地变换而来，没有任何其他东西加进来，很简单，其中Z是一个上边那个常数p(D)，-logZ=-logP(D)，是负对数似然。我们就要最小化J(q)，能够使q近似p*

又因为KL为非负的，所以J(q)是NLL(负对数似然)的上界：

那么进一步变换：

只不过是加了一个负号，变成似然函数的下界，当且仅当q=p*的时候，可以取等号。

不知道看到这里你是不是会有似曾相识的感觉，EM算法不就用另外一个函数来不断优化逼近原分布的极大值的么！！！

EM算法：计算关于隐变量后验概率的期望得到下界；

变分：计算KL散度，得到下界；

相同的思维：不断的迭代，得到更好的下界；

坐标上：不断地上升

目标函数已经出来了，暂时放在这里，接下来要介绍一个很重要的方法：平均场方法。

平均场方法

最流行的的变分方法之一就是平均场近似，在这种方法中，假设后验概率能够近似分解为若干因子的乘积：

我们的目标是最优化问题：

平均场方法使得可以在若干边界分布qi上进行以此优化，说白了就是逐个击破，所以有下边的等式：

从公式中不难看出，要想求qj的对数似然，那么就可以通过求非q的期望加上一个const来近似。

其中，为正则的后验概率：。

这就是平均场方法，接下来就到了本文的重头戏，变分推导！！！！

变分推导

其实把这段公式放在这里我是觉得挺为难的，因为不容易跟大家一一说明每一步是怎么变换过来的，其实不难，就是不太容易想到，邹博先生给我们讲这块的时候我也是听了两遍并且自己手动写了一遍才理解，所以大家最好也消化一下。

我只说一下最后一步：我们得到最后一部这个公式后，然后令：

然后我们可以从第一部分和第二部分中提取公因式q(xi)，其余项在log的作用下变成f(x)/q(x)，我们加一个负号，就得到最终的结果。

很显然是最终结果-KL(q||f)，那么我们既然是想求J(q)的极小值，那么KL(q||f)中的q(x)就应该等于f(x)，最后可以得出这么一个结论：

我们忽略掉归一化因子：

这就是我们的最终结论，就是文章开头给出的那个变分核心公式。

到此，变分算法的理论推理介绍完了，我将会在接下来的一篇文章中介绍变分法的应用。