与SVM的初识(1)：吴恩达视频中的SVM简介

吴恩达视频中的SVM简介

该篇主要参考自吴恩达机器学习视频，部分图片摘自pluskid大神的博客支持向量机系列。同时对于那些和我一样的初学者大力推荐一下pluskid大神的博客,感觉讲得非常清楚。
我的关于SVM系列的博客一共分为三个部分：
1. SVM的具体原理：吴恩达视频中的SVM简介
2. SVM的具体原理：pluskid大神博客SVM系列推导过程简介
3. 对以上两个推导过程的思考和总结

一、吴恩达视频中的SVM

吴恩达视频中对SVM介绍的大体思路是先对logistics regression中的激活函数进行修改，直接给出优化函数，接着讨论这种情况下的优化函数的性质，最后再引入核函数的概念。
1）修改之后的优化函数为：

Min M i n cost=Min c o s t = M i n C∗ C ∗ ∑mi=1[(1−yi)cos0(θT∗xi)+yi∗cos1(θT∗xi)]+∑nj=1θ2j ∑ i = 1 m [ ( 1 − y i ) c o s 0 ( θ T ∗ x i ) + y i ∗ c o s 1 ( θ T ∗ x i ) ] + ∑ j = 1 n θ j 2

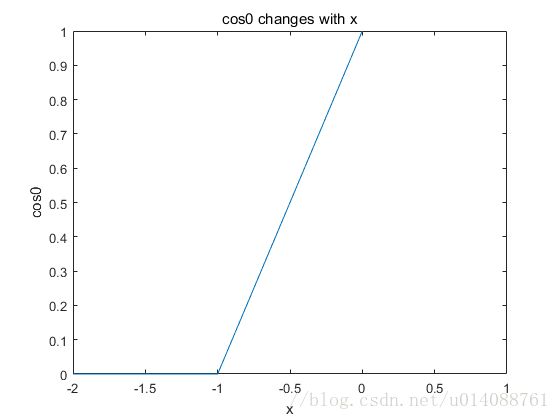
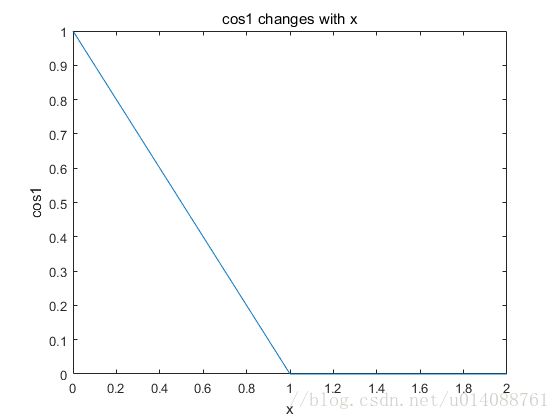
其中,C相当于是logistics regression中的 1λ 1 λ ,m是样本总数,n是特征总数， cos0和cos1函数的图像如下：

接下来考虑C的取值极大的情况，那么第一项应该趋近于零，所以原来的优化函数可以写为以下形式：

Min M i n cost=Min c o s t = M i n ∑nj=1θ2j=∑nj=1||θj||2 ∑ j = 1 n θ j 2 = ∑ j = 1 n | | θ j | | 2

其应当满足的约束条件为：

yi={1,0,θTxi≥1θTxi≤−1   y i = { 1 , θ T x i ≥ 1 0 , θ T x i ≤ − 1    

θTxi可以看成两个向量的内积，可以将其写为以下形式： θ T x i 可 以 看 成 两 个 向 量 的 内 积 ， 可 以 将 其 写 为 以 下 形 式 ：

θTxi=||θ||ki，其中ki是xi在分类超平面法向量θ方向的投影 θ T x i = | | θ | | k i ， 其 中 k i 是 x i 在 分 类 超 平 面 法 向 量 θ 方 向 的 投 影

为了使 θTxi θ T x i 的值满足上述的约束条件，倘若 ki k i 过小的时候，会导致 θ θ 的值必须要取较大的值，很显然这和我们的优化目标相违背。所以， ki k i 的取值应该要取的比较大，那么，应该要使 xi x i 向量和超平面的法向量 θ θ 的方向尽可能一致。在这样的情况下我们就得到了我们所需要的最大间隔的分类器。图形如下所示：

而由上面所得到的分类器明显只能对简单的可线性分离的数据集有效，要想处理线性不可分的情况(如下图所示)。
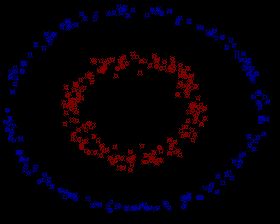
这就需要使用所谓的核函数,当然核函数还具有计算量较小、一般找到的都是全局最优值等特点。这里，主要是以Gaussian核函数为例。Gaussian核函数的形式为

KG(x,x1)=exp(−|x−x1|22σ2 K G ( x , x 1 ) = e x p ( − | x − x 1 | 2 2 σ 2 )

这里我们取x1=[3 5]为例，绘制出Gaussian核函数的图像如下：

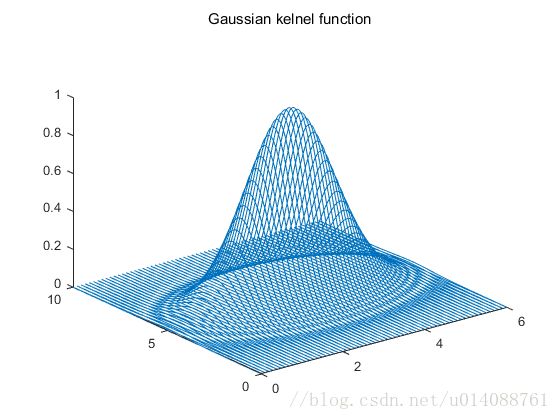
由图像可以很容易得看出核函数的特性为：度量其他点和中心点的相似度。越和中心点相近的点，其函数值越大。
这里的核函数主要的作用是对原数据集进行变换，映射到另一个线性可分的更高维空间中。具体的运用就是将原来空间的一个训练实例 xi x i 带入核函数中分别计算其与若干选定中心点(视频给出的想法是将每一个训练实例作为一个中心点来处理，此时应当有n=m)的相似度 f1、f2、......、fm f 1 、 f 2 、 . . . . . . 、 f m ,即是 xi→ x i → { f1,f2,......,fm f 1 , f 2 , . . . . . . , f m }。最后再对新空间的数据采取进行线性划分。此时对应的新空间的优化函数为：

Min M i n ∑mi=1[yi∗cos1(θTfi)+(1−yi)cos0(θTfi)]+∑nj=1θ2j，and ∑ i = 1 m [ y i ∗ c o s 1 ( θ T f i ) + ( 1 − y i ) c o s 0 ( θ T f i ) ] + ∑ j = 1 n θ j 2 ， a n d n=m n = m

当然，还可以采用其他的核函数进行映射，例如多项式核函数，它的形式如下：

KP(x,x1)=|<x，x1>+d|r K P ( x , x 1 ) = | < x ， x 1 > + d | r

约定俗成的，如果我们不使用其他形式的核函数,即 KL=xT1x K L = x 1 T x ，则称我们使用的是线性核函数。