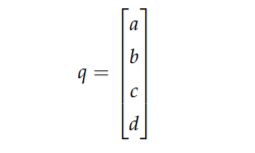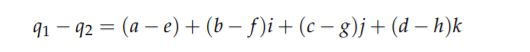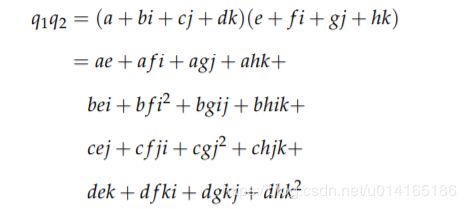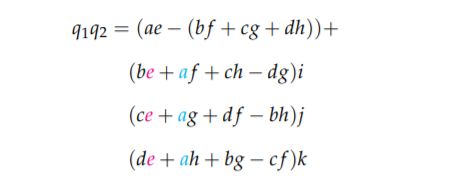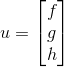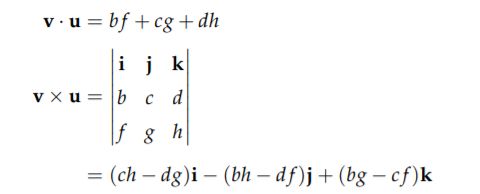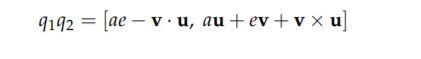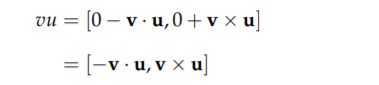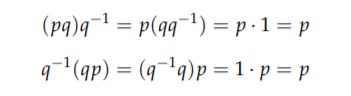3D数学笔记——四元数
四元数
在了解四元数旋转之前，先要了解四元数，所以在此对四元数做个简单的讨论。
- 定义
四元数和复数的定义很相似（但是这里并不打算讨论复数，如果有不明白复数的可以进行百度。），唯一的区别就是四元数有3个虚部，而复数只有一个。所有的四元数q都可以写成一下形式：
q = a + bi + cj +dk
其中
根据该公式得出
与复数类型，因为四元数其实就是对基
的线性组合，四元数也可以写成向量形式
- 模长(范数)
仿照复数的定义，我们可以暂时将一个四元数q = a + bi + cj + dk的模长定义为
![\left \|q \right \|=\sqrt[\sqrt[\sqrt[]{a^2+b^2+c^2+d^2}](http://img.e-com-net.com/image/info8/461dfa07aabe40ee91f4879391b62e4f.gif){kind=small}
还可以表示为 q = [s, v] :
- 加减法
与复数类似，四元数的加法只需要将分量相加就可以了，如果我们有两个四元数q1 = a + bi + cj + dk，q2 = e + f i + gj + hk，那么它们的和为：
减法同理
- 数乘
如果我们有一个四元数 q = a + bi + cj + dk 和一个标量s，那么它们的乘积为：
- 四元数乘法
四元数乘法不遵守交换律，也就是说一般 情况下 
,这也就有了左乘和右乘的区别，如果是q1q2，那么我们就说[q2左乘以q1]，如果是q2q1，那我们就说[q2右乘以q1]. 除了交换律之外，我们经常使用的结合律和分配率在四元数内都是成立的。
那么如果有两个四元数q1 = a + bi + cj + dk 和 q2 = e + f i + gj + hk，那么它们的乘积为
现在我们利用定义中的公式来进行化简
现在我们来把他写成矩阵形式
我们进一步整理公式
注意，如果令
，
，那么
因此q1q2的结果可以用向量点乘和叉乘的形式表示出来
- 纯四元数
在我们正式进入四元数旋转讨论之前，我们还需要更多关于四元数的定义，如果一个四元数能写成这样的形式
那我们则称v是一个纯四元数，既仅有虚部的四元数，因为纯四元数近有虚部的3D向量决定，我们可以将任意的3D向量转换成纯四元数，在本文中，如果一个3D向量v，那么不加粗、没有上标的 v 则为它对应的纯四元数 v = [0, v]．
纯四元数有一个很重要的特性：如果有两个纯四元数v = [0, v], u = [0, u]，那么
- 逆和共轭
因为四元数是不遵守交换律的，我们通常不会将两个四元数相除写为 p q 的形式．取 而代之的是将乘法的逆运算定义为 pq−1 或者 q −1 p，注意它们的结果一般是不同的． 其中，q −1 是 q 的逆（Inverse），我们规定：
这也就是说：
所以，右乘 q 的逆运算为右乘 q −1，左乘 q 的逆运算为左乘 q −1，这个与矩阵的性 质非常相似．
显然，要在无数的四元数中寻找一个满足 qq−1 = q −1 q = 1 的 q −1 是非常困难的， 但是实际上我们可以使用四元数共轭的一些性质来获得 q −1．
我们定义，一个四元数 q = a + bi + ck + dj 的共轭为 q ∗ = a − bi − cj − dk（q ∗ 读作 「q star」）．如果用标量向量有序对的形式来定义的话，q = [s, v] 的共轭为 q ∗ = [s, −v]． 共轭四元数的一个非常有用的性质就是： 
可以看到，这最终的结果是一个实数，而它正是四元数模长的平方：
因为 (q ∗ ) ∗ = [s, −(−v)] = [s, v] = q，
所以我们得到，q ∗ q = qq∗．这个特殊的乘法是遵守交换律的．
如果你还记得之前四元数逆的定义的话：
用这种办法寻找一个四元数的逆会非常高效，我们只需要将一个四元数的虚部改变 符号，除以它模长的平方就能获得这个四元数的逆了．如果 ∥q∥ = 1，也就是说 q 是 一个单位四元数 (Unit Quaternion)，那么：
