深入理解机器学习中拉格朗日乘子和KKT条件

1.引言

本篇博客主要总结了拉格朗日乘子和KTT条件在机器学习中求解最优值的原理，博主尽量举点小例子帮助大家一起共同学习。

2.拉格朗日和KKT作用

我们在求解问题时，经常会遇到一些在约束条件下求解函数的。
在有等式约束条件下，我们选用拉格朗日乘子；
在有不等式约束条件下，选用KKT方法求解最优解。
因此我们可以将KKT条件看成是拉格朗日乘子的泛化。

3.求解最优问题的集中形式

通常我们需要求解的最优化问题有如下几类：

• 无约束条件下求最优值
  minf(x,y)
• 在等式条件下求解最优值
  minf(x,y)
  s.t...g(x,y)=c
• 在不等式条件下求解最优值
  minf(x,y)
  s.t…g(x)<=0,h(x)<=0

4.求解不同最优问题方法

4.1无约束条件下的最优值求解

无约束条件下的函数 f(x,y) 求解最大或者最小值，一般求该函数对各个参数的偏导数，令偏导数为0，求解得到的 x0,y0 即为在该条件下可以使函数 f(x,y) 最优。

αf(x,y)/αx=0

αf(x,y)/αy=0

这样求解的首先需要保证函数 f(x,y) 为凸函数。

4.2 等式条件下的最优值求解（拉格朗日乘子）

假设我们需要求解的函数为 f(x,y) 的最优值，同时需要满足条件 g(x,y)=c ，因此问题就转化为，在 g(x,y)=c 条件下，求解函数 f(x,y) 的最优值。函数 f(x,y)=d 在x,y平面上面具有一些等高线，如下图所示

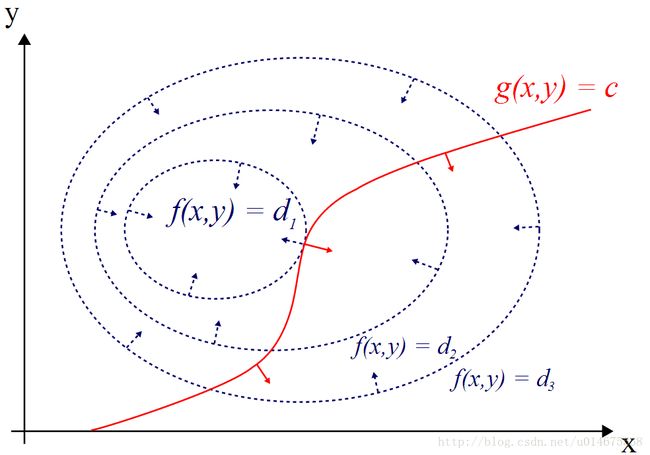
g(x,y)=c 是一条红色的曲线，那么我们在什么样的情况下可以求出他的最优值呢，我们发现函数 g(x,y)=c 会与 f(x,y)=d 相交，那么交点是不是最优值呢，我们以前知识学过，两个函数的交点说明，是两个函数共同的可行解。那最优点怎样求取呢，我们可以更改d的大小，我们得到一系列的等高线。红色曲线与函数 f(x,y)=d 的交点就是最优解。
而拉格朗日乘子就是解决这样问题的，通过引入一个 λ 约束条件 g(x,y)=c 组合得到一个新的函数，这个新函数与目标函数 f(x,y) ，得到最终需要优化函数。

L(x,y,λ)=f(x,y)+λ[g(x,y)−c]

接下来就是求解函数 L(x,y,λ) 对各个参数的偏导数，并令各个偏导数为0，联立可以求出三个参数 x,y,λ ,代入原式，可以求解最优解。

αL(x,y,λ)/αx=0

αL(x,y,λ)/αy=0

αL(x,y,λ)/αλ=0

接下来举一个小例子
f(x,y)=x2y , g(x,y)=x2+y2−1
则可以得到

L(x,y,λ)=f(x,y)+λg(x,y)=x2y+λ(x2+y2−1)

对各个参数求解偏导数得到
2xy+2λx=0
x2+2λy=0
x2+y2−1=0

4.3不等式条件下求解最优解（KKT条件）

对KTT条件的讲解主要采用作者（xianlingmao），对作者表示感谢
对于含有不等式约束的优化问题，如何求取最优值呢？常用的方法是KKT条件，同样地，把所有的不等式约束、等式约束和目标函数全部写为一个式子 L(a,b,x)=f(x)+a∗g(x)+b∗h(x) ，KKT条件是说最优值必须满足以下条件：

• L(a, b, x)对x求导为零；
• h(x) =0;
• a*g(x) = 0;

求取这三个等式之后就能得到候选最优值。其中第三个式子非常有趣，因为 g(x)<=0 ，如果要满足这个等式，必须 a=0 或者 g(x)=0 .
KTT满足的强对偶条件可以这样理解，我们要求 minf(x) , L(a,b,x)=f(x)+a∗g(x)+b∗h(x) ， a>=0 ，我们可以把f(x)写为： maxa,bL(a,b,x) ，为什么呢？因为 h(x)=0,g(x)<=0 ，现在是取 L(a,b,x) 的最大值，a*g(x)是<=0，所以L(a,b,x)只有在a*g(x) = 0的情况下才能取得最大值，否则，就不满足约束条件，因此max_{a,b} L(a,b,x)在满足约束条件的情况下就是f(x)，因此我们的目标函数可以写为 min_x max_{a,b} L(a,b,x)。如果用对偶表达式： max_{a,b} min_x L(a,b,x)，由于我们的优化是满足强对偶的（强对偶就是说对偶式子的最优值是等于原问题的最优值的），所以在取得最优值x0的条件下，它满足 f(x0) = max_{a,b} min_x L(a,b,x) = min_x max_{a,b} L(a,b,x) =f(x0)，我们来看看中间两个式子发生了什么事情：
f(x0) = max_{a,b} min_x L(a,b,x) = max_{a,b} min_x f(x) + a*g(x) + b*h(x) = max_{a,b} f(x0)+a*g(x0)+b*h(x0) = f(x0)

可以看到上述加黑的地方本质上是说 min_x f(x) + a*g(x) + b*h(x) 在x0取得了最小值，用fermat定理，即是说对于函数 f(x) + a*g(x) + b*h(x)，求取导数要等于零，即

f(x)的梯度+a*g(x)的梯度+ b*h(x)的梯度 = 0

这就是kkt条件中第一个条件：L(a, b, x)对x求导为零。

而之前说明过，a*g(x) = 0，这时kkt条件的第3个条件，当然已知的条件h(x)=0必须被满足，所有上述说明，满足强对偶条件的优化问题的最优值都必须满足KKT条件，即上述说明的三个条件。可以把KKT条件视为是拉格朗日乘子法的泛化。