排序2-时间复杂度为O(nlogn)的算法 归并排序 快排
上一篇博文排序1主要讲的是关于评定算法性能的一些指标,以及时间复杂为O(n2)的排序算法。这一篇博文我重点讲述世家复杂度为O(nlogn)的两个经典算法—归并排序 和快排
关于这两个算法 网上的资料很多 在面试中也会经常会被问到(特别是快排),这里我结合自己的理解和总结,写的不好的地方 请多指教。
归并排序(MergeSort)
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
归并排序的核心思想:如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。

我们可以看到归并排序的数据用书的结构来表示后,分和治都是一颗满二叉树,高度为O(log2n)。
分:采用递归的方法进行分解。
将待排序数组中的n个数据分解为n个有序的子数组,采用递归的方法。
首先,我们写出其递推公式及其终止条件:
递推公式:merge_sort(p…r) = merge(merge_sort(p...q),merger_sort(q+1,...r))
终止条件:p>=r
由递推公式写出"分"的代码:
public static void merge_sort(int[] a,int p,int r){
//递归终止条件
if(p>=r) return;
//取p到r之间的中间位置q
int q=(p+r)/2;
//分治递归
merge_sort(a,p,q);
merge_sort(a,q+1,r);
//将a[p,...,q]和a[q+1,..,r]合并为a[p,..,r]
merge(a,p,q,r);
}
治:合并相邻有序子序列
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。

在归并排序中最耗时的就是治(将两个小数组合并为大数组的过程)
治的java代码:
private static void merge(int[] arr,int left,int mid,int right){
int i = left;//左序列指针
int j = mid+1;//右序列指针
int t = 0;//临时数组指针
int[] temp=new int[right-left+1]; //申请一个大小和a[left,..,right]一样大的数组
while (i<=mid && j<=right){
if(arr[i]<=arr[j]){
temp[t++] = arr[i++];
}else {
temp[t++] = arr[j++];
}
}
while(i<=mid){//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while(j<=right){//将右序列剩余元素填充进temp中
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while(left <= right){
arr[left++] = temp[t++];
}
}
归并排序的完整代码
package SortAlgorithm;
/**
* 归并排序(体现分治的思想 利用到递归)
* 归并排序是一个稳定的算法(值相同的元素,再合并前后的先后顺序不变)
归并排序的时间复杂度是O(nlogn),这里值得注意的是,归并排序的执行效率和要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不顾那是最好情况,最坏情况,还是平均情况,时间复杂度都是O(nlogn)
归并排序的空间复杂度是O(n),归并排序是非原地排序算法
* @author xjh 2018.10.22
*/
public class Sort02ToMergeSort {
public static void main(String[] args) {
int[] a={12,2,3,10,4,8,13,3};
int n=a.length;
mergeSort(a,n);
for(int i=0;i=r) return;
//取p到r之间的中间位置q
int q=(p+r)/2;
//分治递归
merge_sort(a,p,q);
merge_sort(a,q+1,r);
//将a[p,...,q]和a[q+1,..,r]合并为a[p,..,r]
merge(a,p,q,r);
}
private static void merge(int[] arr,int left,int mid,int right){
int i = left;//左序列指针
int j = mid+1;//右序列指针
int t = 0;//临时数组指针
int[] temp=new int[right-left+1]; //申请一个大小和a[left,..,right]一样大的数组
while (i<=mid && j<=right){
if(arr[i]<=arr[j]){
temp[t++] = arr[i++];
}else {
temp[t++] = arr[j++];
}
}
while(i<=mid){//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while(j<=right){//将右序列剩余元素填充进temp中
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while(left <= right){
arr[left++] = temp[t++];
}
}
}
归并排序的性能分析
- 1.归并排序是一个稳定的排序算法
在合并的过程中,如果 A[p…q] 和 A[q+1…r] 之间有值相同的元素,那我们可以像伪代码中那样,先把 A[p…q] 中的元素放入 tmp 数组。这样就保证了值相同的元素,在合并前后的先后顺序不变。所以,归并排序是一个稳定的排序算法。 - 2.归并排序的时间复杂度
归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均时间复杂度都是O(nlogn).上图中,我们描述的实质上是2-路归并排序,每次将大数组均等的一分为二,归并时也是将数组两两进行归并。树的高度是O(log2n),每层节点合并的时间复杂度是O(n),所以2-路归并排序的时间复杂度是O(nlog2n) - 3.归并排序的空间复杂度
在归并函数merge()中。我们需要申请而额外的辅助空间占用n个单元,所以归并排序的空格键复杂度是O(n)
快排(QuickSort)
快排是对冒泡排序的一种改进,他也是利用分治的思想。不过,他的思想和归并排序有着很大的区别。
快排的核心思想:如果要排序数组中下标从 p 到 r 之间的一组数据,我们选择p 到 r 之间的任意一个数据作为 pivot(分区点)。
我们遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 的放到右边,将 pivot 放到中间。经过这一步骤之后,数组 p 到 r 之间的数据就被分成了三个部分,前面 p 到 q-1 之间都是小于 pivot 的,中间是 pivot,后面的 q+1 到 r 之间是大于 pivot的。
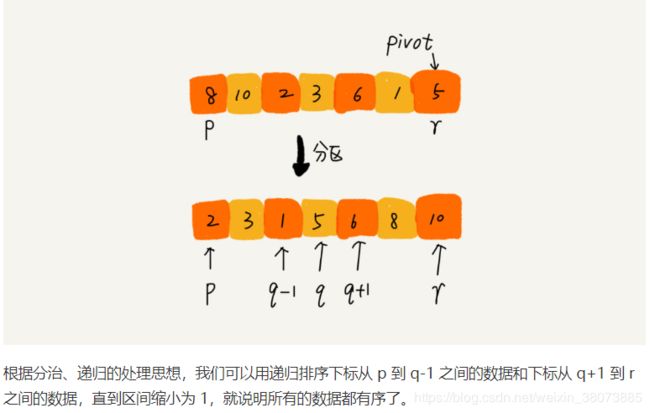
首先我们写出快排的递推公式和终止条件:
递推公式:
quickSort(p,...,r)=quicksort(p,....,q)+quicksort(q+1,....,r)
终止条件:
p>=r
由此我们编程实现期代码:
public static void quickSortInterally(int[] a,int p,int r){
if(p>=r)
return;
int q=partition(a,p,r); //获取分区点
quickSortInterally(a,p,q-1);
quickSortInterally(a,q+1,r);
}
在归并排序中有一个merge()函数,在快排中有一个partition()函数用于划分子数组。这里我们根据严版的教材,java实现了一个分区函数。
public static int partition(int[] a,int p,int r){
//这里写一个好简单的分区函数(每次子数组中的首个元素作为分区点)
int pivot=a[p];
while (p=pivot) --r;
a[p]=a[r]; //从后往前遍历 找到小于分区点的值 将其移动到分区点的左侧
while (p 这里实现的partition()函数没有像归并排序的merger()函数一样需申请额外的内存空间,它的空间复杂度是O(1),属于原地排序算法。
快排的完整代码
package SortAlgorithm;
/**
* 快排
* @author xjh 2-18.10.22
*/
public class Sort02ToQuickSort {
public static void main(String[] args) {
int[] a={12,2,3,10,4,8,13,3};
int n=a.length;
quickSort(a,n);
for(int i=0;i=r)
return;
int q=partition(a,p,r); //获取分区点
quickSortInterally(a,p,q-1);
quickSortInterally(a,q+1,r);
}
public static int partition(int[] a,int p,int r){
//这里写一个好简单的分区函数(每次子数组中的首个元素作为分区点)
int pivot=a[p];
while (p=pivot) --r;
a[p]=a[r]; //从后往前遍历 找到小于分区点的值 将其移动到分区点的左侧
while (p 快排的性能分析
- 1.快排是一种不稳定的排序算法
快排中,经过分区操作,原数组中的值相同的元素相对位置极大可能发生改变,所以快排是一种不稳定的排序算法。 - 2.快排的时间复杂度
快排的时间开销很大程度上取决于分区点的设置。理想情况下,每次分区操作,我们选择的 pivot 都很合适,正好能将大区间对等地一分为二。但实际上这种情况是很难实现的。快排的平均时间复杂度是O(nlogn)。最坏情况下,如果数组中的数据原来已经是有序的了,比如 1,3,5,6,8。如果我们每次选择最后一个元素作为 pivot,那每次分区得到两个区间都是不均等的。我们需要进行大约 n 次分区操作,才能才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 元素,这种情况下,快排的时间复杂度就从 O(nlogn) 退化成了O(n2)。 - 3.快排的空间复杂度
前面我们已经提到快排不需要申请额外的内存空间。它的空间复杂度是O(1),这也是为什么归并排序任何情况下的时间复杂度是O(nlogn),但是快排却在实际应用中应用的比归并排序广泛。
归并排序和快排的区别
虽然二者都是属于 分治思想的排序算法,平均时间度都为O(nlogn),但是二者还是有很大区别。
- 1.归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法,但是它是非原地排序算法。我们前面讲过,归并之所以是非原地排序,主要原因是合并函数无法在原地执行。
- 2.快速排序通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题。
彩蛋(面试常考题)
快排在程序员面试中属于高频出现的基础算法知识了,这里总结一个如何利用快排在O(n)内查找到第k大的数据??
注意这里只需要让我们找到第k大的元素,我们不需要将数据中的元素全部排序有序状态,也不关心第1到第k-1的元素顺序。
比如,6,1,3,5,7,2,4,9,11,8 这样一组数据,第 3 大是8。
如果我们选择数组区间 A[0…n-1] 的最后一个元素 A[n-1] 作为 pivot,对数组 A[0…n-1] 原地
分区,这样数组就分成了三部分,A[0…p-1]、A[p]、A[p+1…n-1]。
如果 p+1=K,那 A[p] 就是要求解的元素;如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1] 区间,我们再按照上面的思路递归地在 A[p+1…n-1] 这个区间查找。同理,如果K
这里有种方法,每次将待定数组中的最大值遍历得到提取出来,提取k次得到的值不就是第k大的元素吗?? 但是注意,这种方法每次遍历都有n的线性级,一共有k次,所以时间复杂度时O(k*n).当k比较小时,1 或者2 那他的时间消耗还好,倘若k为n/2或者更大时,时间消耗时不可估量的,大到O(n2)
当然以上讲解的是一种思路,查找TopK元素的方法还有其他方法,例如小顶堆。
后续会继续更新,写的不好之处,望能指出,共同进步…
部分内容参考:图解排序算法(四)之归并排序