机器学习基础练习题（3）支持向量机

作业题目

在本次作业中我们需要利用支持向量机（SVM）方法将数据集中的图片分为两类。数据集中的图片分为彩色图片和黑白图片，要求实现线性SVM模型、松弛SVM模型和非线性SVM模型，并进行比较。（对这个题目真的无语，不用SVM其实更好分）

图片预处理

由于直接处理图像数据量过大，每个像素点都包含不同的数据，而且每张图片的像素并不相同，所以我们有必要对图片进行预处理，提取图像中的关键信息。
直观来看，彩色图片与黑白图像在色彩上差异很大，彩色图片具有更丰富的颜色信息。这种区别体现在RGB通道上为：彩色图像的RGB三通道值均不相等，黑白图像的RGB三值相等。
我们可以提取图片的各通道均值和均方差，并分别对三个通道的均值和均方差再取均值，作为图片的特征值。从提取结果来看，以图像均值和均方差为横纵坐标，黑白图像的坐标点十分集中，而彩色图像的坐标点比较分散。

SVM训练

SVM原理

SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如下图所示，wx+b=0即为分离超平面，对于线性可分的数据集来说，这样的超平面有无穷多个，但是几何间隔最大的分离超平面却是唯一的。

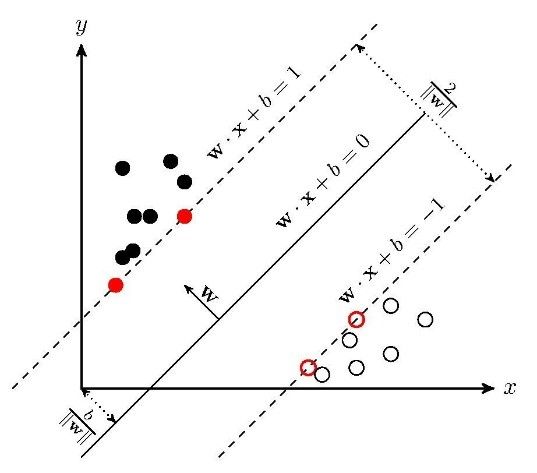
上图中二分类的点都位于分离超平面的两侧，直接通过线性SVM便可以完成分类，但实际情况中，往往不同的点事是交织在一起的，无法直接通过线性模型进行分类，我们需要借助非线性变换将它转化为某个维度的特征空间中的线性分类问题，在高维特征空间中学习线性支持向量机。由于在线性支持向量机学习的对偶问题里，目标函数和分类决策函数都只涉及实例和实例之间的内积，所以不需要显式地指定非线性变换，而是用核函数替换当中的内积。核函数表示，通过一个非线性转换后的两个实例间的内积。

sklearn.svm

SVM是支持向量机（Support Vector Machine）的简称。SVM具有分类功能（SVC，C是Classification的首字母）；也具有回归功能（SVR，R是Regression的首字母）。在python的库sklearn中有SVM的相关操作，我们可以直接利用其中的SVC函数进行黑白图片的二分类。
函数名：
sklearn.svm.SVC(C=1.0, kernel=‘rbf’, degree=3, gamma=‘auto’, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=None, random_state=None)
参数：
l C：C-SVC的惩罚参数C 默认值是1.0
C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。
l kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’
　　0 – 线性：u’v
　　 1 – 多项式：(gamma*u’v + coef0)^degree
　　2 – RBF函数：exp(-gamma|u-v|^2)
　　3 –sigmoid：tanh(gammau’*v + coef0)
l degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。
l gamma ： ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’，则会选择1/n_features
l coef0 ：核函数的常数项。对于‘poly’和 ‘sigmoid’有用。
l probability ：是否采用概率估计.默认为False
l shrinking ：是否采用shrinking heuristic方法，默认为true
l tol ：停止训练的误差值大小，默认为1e-3
l cache_size ：核函数cache缓存大小，默认为200
l class_weight ：类别的权重，字典形式传递。
l verbose ：允许冗余输出
l max_iter ：最大迭代次数。-1为无限制。
l decision_function_shape ：‘ovo’, ‘ovr’ or None, default=None3
l random_state ：数据洗牌时的种子值

python代码实现

首先，通过get_imagines()函数获取训练（测试）用到的图片，该函数会将目标文件夹下的所有后缀为“jpg”，“bmp”的文件放在一个列表中返回。
之后，对获取到的每张图片，我们利用OpenCV中的函数meanStdDev()直接获取图像三个通道的均值和均方差，之后再利用numpy中的求均值函数得到整张图片的均值和均方差。再利用sklearn.svm中的SVC函数建立支持向量机分类模型，将训练数据和label作为参数输入得到模型，同时，我们可以通过修改SVC函数的相关参数以实现不同的分类模型。
最后，将测试数据代入模型中验证，并通过plot函数画出支持向量机的支持向量，和边界曲线。

结果验证

线性SVM模型

将SVC中的参数kernel定为‘linear’便可以实现线性SVM模型，同时可以通过coef_参数得到线性SVM模型的系数。画出支持向量机分类分类示意图如下所示：
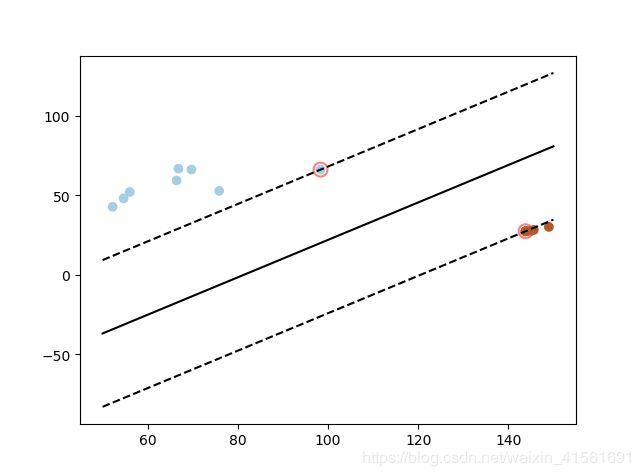上图中红圈圈出的点即为支持向量点，虚线为过两个支持向量点距离最大的一对平行曲线，二者中间的实心曲线为分离超平面。同时，由上图我们可以看出，彩色图片和黑白图片特征值差异明显，可以直接通过基础的线性SVM模型完成二分类。

RBF SVM模型

更改kernel为“rbf”便可实现非线性SVM模型中的RBF（高斯核函数）模型。下式为高斯核核函数：
$$K(x,y)=e^{-\gamma ||x-y|{|}^2}$$
高斯核本质是在衡量样本和样本之间的“相似度”，在一个刻画“相似度”的空间中，让同类样本更好的聚在一起，进而线性可分。所以在SVM中，更多使用的核函数为高斯核函数。利用高斯核函数得到的支持向量示意图如下：

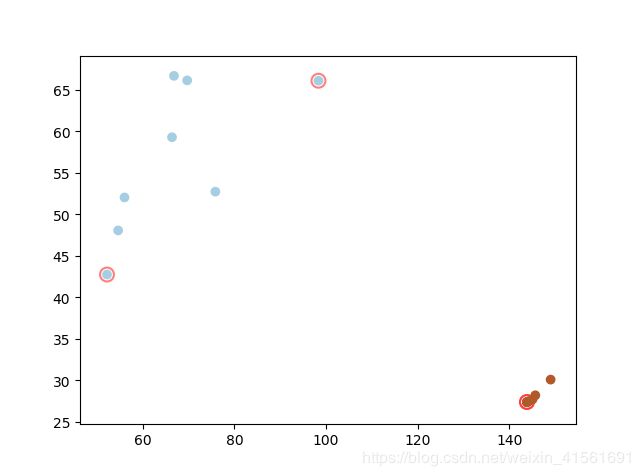
多项式SVM模型

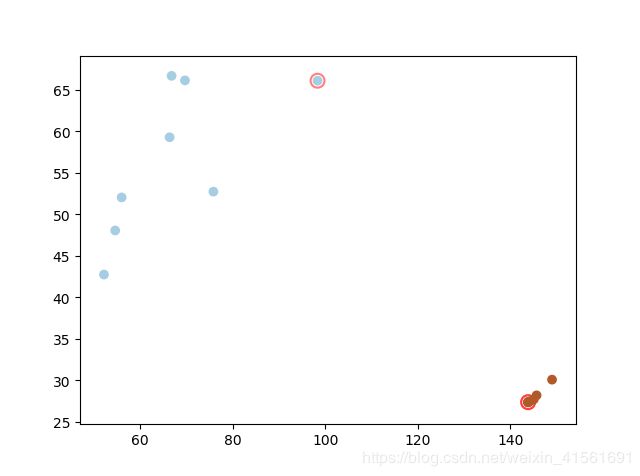
由于本问题中的模型不需要任何的升维操作，直接是线性可分的，所以采用多项式核函数的结果和线性SVM的结果差异不大。下图为多项式核SVM预测结果，同样完全正确。

python代码

import os
import sys

import cv2
import numpy as np
import pylab as pl

from sklearn import svm, metrics

sys.path.append(os.getcwd())

def get_images(type='train'):
    files = []
    exts = ['jpg','bmp']
    if type == 'train':
        path = 'C:/Users/gyl/Desktop/pic/'
    else:
        path = 'C:/Users/gyl/Desktop/test/'
    for parent, dirnames, filenames in os.walk(path):
        for filename in filenames:
            for ext in exts:
                if filename.endswith(ext):
                    files.append(os.path.join(parent, filename))
                    break
    print('Find {} images'.format(len(files)))
    return files

def main():
    im_fn_list = get_images(type='train')
    means_of_pics = []
    for im_fn in im_fn_list:
        #print('===============')
        #print(im_fn)
        try:
            src = cv2.imread(im_fn)
        except:
            print("Error reading image {}!".format(im_fn))
            continue
        means, dev = cv2.meanStdDev(src)
        means = np.mat(means[0:2])
        dev = np.mat(dev)
        means_of_pics.append([np.mean(means),np.mean(dev)])
    means_of_pics = np.reshape(means_of_pics,(16,2))
    #print(means_of_pics)
    label = np.vstack((np.zeros((8,1),dtype=int), np.ones((8,1),dtype=int)))
    label = np.reshape(label,(16,1))
    #print(label)
    train_data = np.vstack((means_of_pics))
    '''plot the line'''
    clf = svm.SVC(C=1.0,kernel='linear')
    clf.fit(train_data, label)

    Y = [0]*8 +[1]*8
    
    w = clf.coef_[0]
    a = -w[0]/w[1]
    xx = np.linspace(50,150)
    yy = a*xx - (clf.intercept_[0])/w[1]
    b = clf.support_vectors_[0]
    yy_down = a*xx + (b[1] - a*b[0])
    b = clf.support_vectors_[-1]
    yy_up = a*xx + (b[1] - a*b[0])

    pl.plot(xx, yy, 'k-')
    pl.plot(xx, yy_down, 'k--')
    pl.plot(xx, yy_up, 'k--')
    

    for i in clf.support_:
        pl.scatter(train_data[i, 0], train_data[i, 1], s=100, c = '', alpha=0.5, linewidth=1.5, edgecolor='red')
    pl.scatter(train_data[:, 0], train_data[:, 1], c=Y, cmap=pl.cm.Paired)
    pl.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],s=80, facecolors='none')
    pl.show()

    print("clf.support_vectors_:")
    print(clf.support_vectors_)
    print("clf.support_:",clf.support_)
    print("clf.n_support_:",clf.n_support_)

    im_test_list = get_images(type='test')
    test_list = []
    for im_test in im_test_list:
        try:
            src = cv2.imread(im_test)
        except:
            print("Error reading image {}!".format(im_fn))
            continue
        means, dev = cv2.meanStdDev(src)
        means = np.mat(means[0:2])
        dev = np.mat(dev)
        test_list.append([np.mean(means),np.mean(dev)])
    print("prediction result:")
    print(clf.predict(test_list))
        


main()