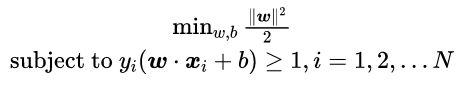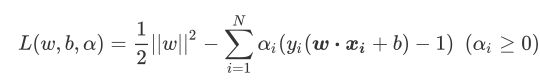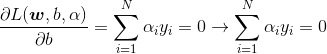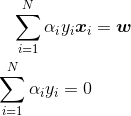【精简推导】支持向量机（拉格朗日乘子法、对偶函数、KKT条件）

支持向量机，就是通过找出边际最大的决策边界，来对数据进行分类的分类器。因此，支持向量分类器又叫做最大边际分类器。

（疯狂暗示：这是一个最优化问题啊~）

直接上目标求解函数：

这个式子是支持向量机基本形（这个目标式子的由来可以参考西瓜书）。一看这就是一个二次凸优化问题，虽然可以直接用优化包求解，但是效率不高，而且对于后面引入核函数也不方便。因此我们习惯用拉格朗日乘子法求解这个优化问题。

故事从这里开始：

高等数学教过：求解带约束条件的最优化问题，可以用拉格朗日乘子法，因此上式求解可以写成：

上式是拉格朗日乘子，而  和  都是我们已知的特征矩阵和标签。拉格朗日函数分为两部分。第一部分是我们的原始损失函数，第二部分加了不等式的约束条件。我们希望， 不仅能够代表我们原有的损失函数 和约束条件，还能够表示我们想要最小化损失函数来求解 和 ，所以我们要先以 为参数，求解 的最大值，然后再以 和 为参数，求解 的最小值。因此，我们的目标可以写作：

--------------------------------------------------【插曲】为什么拉格朗日能转化成其对偶函数？--------------------------------------------------------

对于任何一个拉格朗日函数：

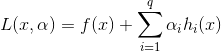，都存在一个与它相对应的对偶函数,只带有拉格朗日乘子作为它的唯一参数。如果这个的最优解存在，并可以表示为min，并且对偶函数的最优化也存在，并可以表示为,则我们可以定义一个对偶差异，拉格朗日函数的最优解与其对偶函数的最优解之间的差异值，：

如果，则称与其对偶函数之间存在强对偶关系。此时我们就可以通过求解对偶函数的最优解来替代求解原始函数的最优解。

什么时候强对偶关系存在？答：拉格朗日必须满足KKT条件：

首先是所有的一阶导数必须为0，其次约束条件中的函数小于等于0，再其次，拉格朗日乘子大于等于0，以及约束条件乘以拉格朗日乘子必须等于0（即，不同i的取值下，两者之间至少有一个为0）。当所有限制都被满足，则拉格朗日函数 的最优解与其对偶函数的最优解相等，我们就可以将原始的最优化问题转换成为对偶函数的最优化问题。

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------

先来求解拉格朗日函数：

分别对和求导：

       （1）

     （2）

（我们发现两个导数的结果中都有，因此到这里还是无法求出和。把1式和2式带入到拉格朗日函数，我们得到一个只含有未知数的式子，这个式子被称为拉格朗日对偶函数。把对偶函数的结果求解出来，再带入到1,2就得到了w和b的解）

为了把拉格朗日函数转成其对偶问题，我们来看看其是否满足强对偶关系。

其一：我们在上面已经求导让拉格朗日函数对w，b求导等于0，得到式子：

(一阶导数必须为0,第一个条件满足。)

其二：由于最开始的约束有：，

因此拉格朗日中约束条件 （约束条件函数小于0，第二个条件满足）

其三：拉格朗日乘子，天然满足。

其四：所以随后之剩下约束条件乘以拉格朗日乘子是否等于0成了:

这个条件很容易满足，能够让的点，就是落在虚线平面上的样本点，也就是支持向量。

所有不是支持向量的样本点必须满足。满足这个式子，说明了我们求解的函数w,b以及超平面存在，只与支持向量有关，与其他样本点无关。现在KKT条件的四个都满足了，现在可以使用的对偶函数来求了。求得了再带入1,2式子就搞定了。

转换成对偶形式：

带入2式有：

带入1式有：

令两个w来源于不同的特征和标签：

将矩阵相乘成内积形式：

函数就是我们的对偶函数，对所有存在对偶函数的拉格朗日函数，有对偶差异，表示如下：

则对于我们的和有：

而对于求偏导并让偏导为0，其实是在求解最小值，所以可以把公式写成：

由于所有的KKT条件满足，因此对偶差异。

如此，我们只需要求解对偶函数的最大值，就可以求出 了。最终我们的目标函数变为：

到了这一步，我们就需要使用梯度下降，SMO或者二次规划(QP，quadratic programming)来求解了。

求得参数之后，把w,b带入带决策边界的表达式子中。当我们有一个新的样本需要被划分，这个时候把这样本的值带进去就可以求解了：

为任意待分类样本。sign是符号函数，中间的值>0返回1，<0则返回-1。

 

以上这个些是处理数据在低维空间是线性可能的情况，如果数据在低维空间中线性不可分，则需要引入核函数。这里就不详细说明核函数的。

我们只要知道，当支持向量机遇到线性不可分数据的时候，可以通过核函数，将原本低维空间线性不可分的数据映射到高维空间中，从而实现线性可分。如下图：

也就是说：核函数的价值在于它虽然是将特征进行从低维到高维的转换，但核函数绝就绝在它实际是在低维上进行计算，却将效果表现到了高维上，也就是避免了直接在高维空间中复杂计算（想一想本来特征维度很高，还要升高维度，那就是很可怕的计算量）。