理解回溯算法——回溯算法的初学者指南
0 前言
最近做了不少关于回溯法的算法题,积累了一些心得,这篇博文算是对回溯法的一个小总结。
1 回溯法简介
回溯法简单来说就是按照深度优先的顺序,穷举所有可能性的算法,但是回溯算法比暴力穷举法更高明的地方就是回溯算法可以随时判断当前状态是否符合问题的条件。一旦不符合条件,那么就退回到上一个状态,省去了继续往下探索的时间。
最基本的回溯法是在解空间中穷举所有的解。比如求序列[1,2,3]的全排列,那么我们可以画出一颗解空间树。
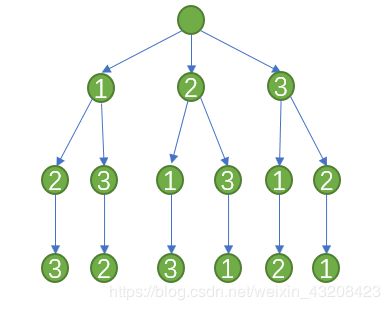
回溯法的特点是深度优先遍历,也就是该问题的遍历顺序是1->2->3,然后从子节点3返回,从子节点2返回,再到1->3->2,以此类推。
状态的返回只有当前的节点不再满足问题的条件或者我们已经找到了问题的一个解时,才会返回,否则会以深度优先一直在解空间树内遍历下去。
当然,对于某些问题如果其解空间过大,即使用回溯法进行计算也有很高的时间复杂度,因为回溯法会尝试解空间树中所有的分支。所以根据这类问题,我们有一些优化剪枝策略以及启发式搜索策略。
所谓优化剪枝策略,就是判断当前的分支树是否符合问题的条件,如果当前分支树不符合条件,那么就不再遍历这个分支里的所有路径。
所谓启发式搜索策略指的是,给回溯法搜索子节点的顺序设定一个优先级,从该子节点往下遍历更有可能找到问题的解。
2 回溯函数的组成
1.回溯出口,当找到了一个问题的解时,存储该解。
2.回溯主体,就是遍历当前的状态的所有子节点,并判断下一个状态是否是满足问题条件的,如果满足问题条件,那么进入下一个状态。
3.状态返回,如果当前状态不满足条件,那么返回到前一个状态。
def backtrack(current_statement) -> bool:
if condition is satisfy:
solution = current_statement
return True
else:
for diff_posibility in current_statement:
next_statement = diff_posibility
if next_statement is satisfy condition:
if backtrack(next_statement):
return True
else:
back to current_statement
return False
3 简单的回溯函数
3.1 问题描述
给定一个不包含重复数字的序列,返回所有不重复的全排列。
3.1.1 问题分析
遍历所有的解空间树即可找到答案。
首先定义一个回溯函数
# combination 为当前的状态
backtrack(combination=[])
那么它的出口部分也很好写,就是当combination的长度等于序列的长度时,就找到了问题的一个解。
if len(combination) == len(nums):
answer.append(combination)
然后是回溯函数的主体部分,我们要遍历当前状态下的所有子节点,并判断子节点是否还符合问题的条件,那么对于这个问题,因为全排列的数是不能够重复的,所以我们的判断方式是当前的数没有包含在combination中,那么进入下一个状态。
for num in nums:
if num not in combination:
backtrack(combination+[num])
那么这个问题需要返回上一个状态吗?答案是不需要,因为backtrack的下一个状态的写法是backtrack(combination + [num]),这并不会改变我们当前的combination的值,因为我们没有对combination对象进行一个重新的赋值操作。
如果说修改一下回溯函数的主体。
for num in nums:
if num not in combination:
combination.append(num)
backtrack(combination+[num])
那么这时候,combination的值被改变了,所以需要写一个返回上一个状态的代码。
for num in nums:
if num not in combination:
combination.append(num)
backtrack(combination)
combination.pop()
并且,因为我们传入的是相当于是combination对象,所以在存储解的时候需要深拷贝。
if combination.__len__() == nums.__len__():
solution = copy.deepcopy(combination)
answer.append(solution)
3.1.2 完整代码
import copy
class Solution:
def permute(self, nums: list):
answer = []
def backtrack(combination=[]):
if combination.__len__() == nums.__len__():
solution = copy.deepcopy(combination)
answer.append(solution)
return
for num in nums:
if num not in combination:
combination.append(num)
backtrack(combination)
combination.pop()
backtrack()
return answer
3.2 问题描述
给定一个包含重复数字的序列,返回所有不重复的全排列。
3.2.1 问题分析
相对于第一个问题,这个问题稍微加了点难度,也就是序列中包含了重复的数字。由于有重复数字的关系,我们也就不能够只简单的判断一下某个数是否在combination中。我们可以构建一个hash表,来记录当前状态的hash键值。
hash_num = {}
for item in nums:
hash_num[item] = hash_num.get(item,0) + 1
在回溯函数中,我们用hash表来判断是否可以将当前的数字加入到combination中。
def backtrack(combination:list=[],hash_num:dict=hash_num):
if len(combination) == len(nums):
output.append(combination)
else:
for num_key in list(hash_num.keys()):
hash_num[num_key] = hash_num[num_key] - 1
if hash_num[num_key] == 0:
hash_num.pop(num_key)
backtrack(combination + [num_key],hash_num)
hash_num[num_key] = hash_num.get(num_key,0) + 1
如果当前的数字在hash表中对应的值是1,那么进入到下一个状态之前,我们要删掉这个hash_key。
之后要注意把这个hash_table恢复回原来的状态。
3.2.2 完整代码
class Solution:
def permuteUnique(self, nums: list) -> list:
hash_num = {}
for item in nums:
hash_num[item] = hash_num.get(item,0) + 1
output = []
def backtrack(combination:list=[],hash_num:dict=hash_num):
if len(combination) == len(nums):
output.append(combination)
else:
for num_key in list(hash_num.keys()):
hash_num[num_key] = hash_num[num_key] - 1
if hash_num[num_key] == 0:
hash_num.pop(num_key)
backtrack(combination + [num_key],hash_num)
hash_num[num_key] = hash_num.get(num_key,0) + 1
backtrack()
return output
4 剪枝对于回溯函数的重要性
像是对于某些问题,如果要搜索全部的解空间的话,范围太大,如果能提前根据问题的特征排除某些不必要搜索的子空间,将大大的提高搜索效率。
4.1 问题描述
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取,并且所有数字(包括 target)都是正整数,解集不能包含重复的组合。
在某种意义上,如果对这个问题不进行剪枝,那这个问题的搜索空间是无限的。
4.1.1 问题分析
首先,因为candidates是可以重复选择的,所以在每个状态下,都有len(candidates)个子节点。
首先将candidates进行升序排序。
我们从根结点出发,选择一个子节点之后,加上将这个子节点的值,作为下一个状态,在遍历的过程中对遇到的值进行累加。
如果在某个状态下:
1.我们发现此时的状态代表的数值等于我们的target,那么它的右兄弟结点以及以它为根结点的子树不再进行探索。
2.我们发现此时的状态代表的数值要小于我们的target,那么继续进行探索。
3.我们发现此时的状态代表的数值要大于我们的target,那么它的右兄弟结点以及以它为根结点的子树不再进行探索。

如上图所示,我们对遇到的结点进行累加,如果发现有一个结点的值是我们target的值,因为candidates的值是按照升序排序的,并且candidates的数值不可能重复,那么它的右兄弟结点的状态值只能够大于target。candidates中的值只包含正数,因此,以它为根结点的子树下的所有结点的状态值都会大于target,因此这些结点我们都没有必要进行探索了。
同理,如果我们发现当前结点的状态值要大于我们的target值,那么其右兄弟结点的状态值,以及以它为根节点的子树下的所有结点的状态值都会大于target,因此这些结点也是没有必要探索的。
根据这些限制条件,我们可以大大的缩小我们搜索的子空间,提高问题解答的效率。
4.1.2 完整代码
class Solution:
def combinationSum(self, candidates: list, target: int) -> list:
candidates = sorted(candidates)
answer = []
def backtrack(current_sum:int=0,current_list:list=[]):
if current_sum == target:
if sorted(current_list) not in answer:
answer.append(current_list)
else:
for number in candidates:
if current_sum + number > target:
break
else:
backtrack(current_sum+number,current_list+[number])
backtrack()
return answer
4.2 问题描述
给出集合 [1,2,3,…,n],其所有元素共有 n! 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:
“123”
“132”
“213”
“231”
“312”
“321”
给定 n 和 k,返回第 k 个排列,其中给定 n 的范围是 [1, 9],给定 k 的范围是[1, n!]。
4.2 问题分析
这个问题是能够更加的突显剪枝的重要性,如果不对问题进行剪枝,我们也可以很容易的对问题进行求解:对找到的解进行计数,当找到第k个解时,停止回溯算法,返回结果即可。
代码1-无剪枝算法
import time
class Solution:
def getPermutation(self, n: int, k: int) -> str:
number_list = []
for i in range(n):
number_list.append(str(i+1))
answer = []
count = [0]
def backtrack(combination,k):
if count[0] == k:
return None
if len(combination) == len(number_list):
temp = count[0]
count[0] = temp + 1
if count[0] == k:
answer.append(combination)
return None
else:
for number in number_list:
if number not in combination:
backtrack(combination + number,k)
backtrack("",k)
return answer[0]
if __name__ == '__main__':
start_time = time.time()
print(Solution().getPermutation(9,362880))
end_time = time.time()
print('run time:',end_time-start_time)

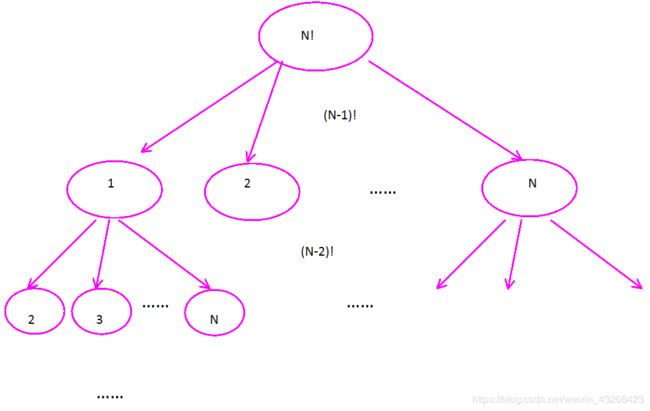
如果再次分析这个问题,其实它有一定的规律,对于N个数的全排列而言,如果我们对所有可能性做一个分区的话。当第一个数确定了,那么以其为根结点所代表的的解空间有(N-1)!个。对于1而言,它的剩下的解在全排列中的位置是[1,(N-1)!],对于2而言,它的剩下的解在全排列中的位置是[(N-1)!+!,2*(N-1)!],以此类推。
首先我们找到K对应的解空间的区间。假设此时找到对应的区间是a,我们要更新我们的K值,K = K - (a-1)*(N-1)!。
然后进入这个子树,以子树为根,它的第一层结点可以确定第二个数。因为如果排列的第二个数确定后,那么以其为根节点的子树所代表的解空间共有(N-2)!个解。我们可以进一步缩小K的范围,K = K - (b-1) * (N-2)!。
直到找到K = 0的情况,那么深度优先遍历到终点,返回此时的找到的解就是第k个排列。
代码2-剪枝算法
import time
class Solution:
def getPermutation(self, n: int, k: int) -> str:
dit = {0:1 ,1: 1, 2: 1, 3: 2, 4: 6, 5: 24, 6: 120, 7: 720, 8: 5040, 9: 40320}
number_list = []
for i in range(n):
number_list.append(str(i+1))
answer = []
def backtrack(combination,n,k):
if len(combination) == len(number_list):
answer.append(combination)
return None
else:
for number in number_list:
if number not in combination:
current_possibility = dit[n]
if k - current_possibility > 0:
k = k - current_possibility
else:
backtrack(combination + number,n-1,k)
return None
backtrack("",n,k)
return answer[0]
if __name__ == '__main__':
start_time = time.time()
print(Solution().getPermutation(9,362880))
end_time = time.time()
print('run time: %.17f' % (end_time - start_time))
5 启发式搜索对于回溯函数的重要性
5.1 问题描述
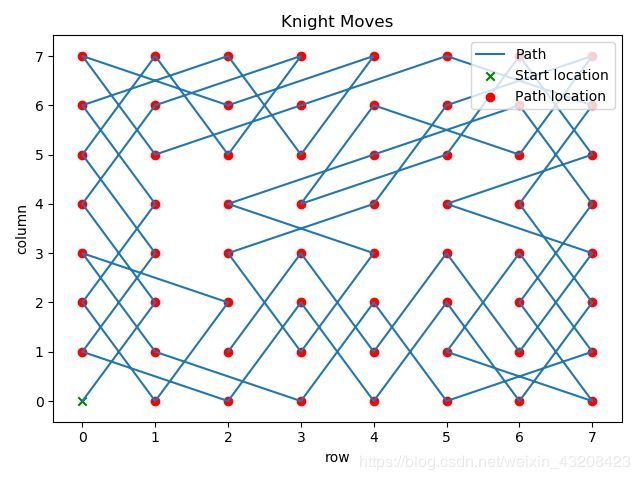
在 8 × 8 方格的国际象棋棋盘上,骑士从任意指定的方格出发,以跳马规则(横一步竖两步或横两步竖一步),周游棋盘的每一个格子,要求每个格子只能跳过一次。

5.2 问题分析
骑士巡游问题的一个启发式搜索策略是将当前的子节点排一个序,按照当前子节点的邻接格子的个数从小到大排序,这个搜索策略就是先尽量遍历棋盘的边缘,到后期骑士自然而然会遍历棋盘中间,到那时候中间可走的路径要更多,从而更有可能找到问题的解。
首先我们要判断当前的位置下,骑士能够走的下一个合法位置(不能够超过棋盘的边界,并且是一个完全没有走过的新位置),然后记录下一个位置的邻接格子的个数并按照这个进行排序。
这种搜索策略算是一种基于贪心算法的策略,其优点是能够加快我们寻找一种解的速度,但是其缺点是对于全部解而言,仍然没有起到一个加速的作用。
5.3 完整代码
import matplotlib.pyplot as plt
class Solution:
def knight_moves(self,start_location):
answer = []
answer.append(start_location)
board = [[0 for _ in range(8)] for _ in range(8)]
board[start_location[0]][start_location[1]] = 1
def backtrack(current_location):
if len(answer) == 64:
return True
next_node = self.choose_node(board,current_location)
for next_location in next_node:
answer.append(next_location)
board[next_location[0]][next_location[1]] = 1
if backtrack(next_location):
return True
else:
answer.pop()
board[next_location[0]][next_location[1]] = 0
return False
backtrack(start_location)
return answer
def not_touch(self,next_location):
if next_location[0] in range(0,8) and next_location[1] in range(0,8):
return True
else:
return False
def move(self,current_location,mode):
a = current_location[0]
b = current_location[1]
if mode == 1:
next_location = [a-1,b+2]
elif mode == 2:
next_location = [a+1,b+2]
elif mode == 3:
next_location = [a-2,b-1]
elif mode == 4:
next_location = [a-2,b+1]
elif mode == 5:
next_location = [a-1,b-2]
elif mode == 6:
next_location = [a+1,b-2]
elif mode == 7:
next_location = [a+2,b-1]
else:
next_location = [a+2,b+1]
return next_location
def choose_node(self,board,current_location):
nodes = []
for mode in range(1,9):
next_location = self.move(current_location,mode)
if self.not_touch(next_location) == True and board[next_location[0]][next_location[1]] == 0:
number_nor = self.number_nor(next_location)
nodes.append([next_location,number_nor])
nodes = sorted(nodes,key=lambda x:x[1])
new_nodes = []
for item in nodes:
new_nodes.append(item[0])
return new_nodes
def number_nor(self,location) -> int:
if location == [0,0] or location == [7,7] or location == [0,7] or location == [7,0]:
return 2
if location[0] == 0 or location[0] == 7 or location[1] == 0 or location[1] == 7:
return 3
else:
return 4
if __name__ == '__main__':
ans = Solution().knight_moves([0,0])
x = [item[0] for item in ans]
y = [item[1] for item in ans]
plt.plot(x,y,label='Path')
plt.xlabel('row')
plt.ylabel('column')
plt.title('Knight Moves')
plt.scatter(x[0],y[0],c='green',marker='x',label='Start location')
plt.scatter(x[1:],y[1:],c='red',label='Path location')
plt.legend(loc='best')
plt.show()
6 用回溯算法解决一些经典的问题
6.1 解数独
6.1.1问题描述
数独是源自18世纪瑞士的一种数学游戏。是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(3*3)内的数字均含1-9,不重复 。
数独盘面是个九宫,每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件,利用逻辑和推理,在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次,所以又称“九宫格”。
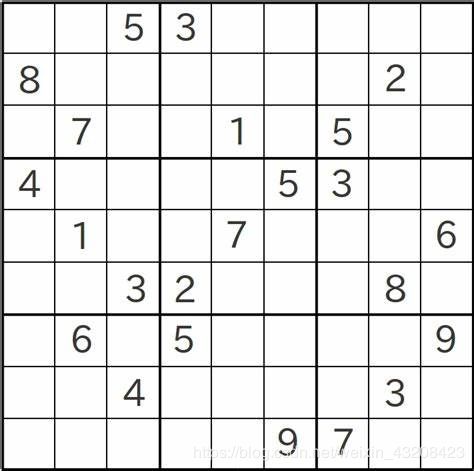
6.1.2 问题分析
首先,根据数独的规则,如果我们在某个空格填了一个数字,那么该数字所在的行与列还有九宫格不能够与原来的数字重复,根据这个特点,可以大大的减少我们需要计算的组合数。
然后用回溯法对所有组合进行判断,如果遇到不满足条件的数字组合,要回退到上一个合法状态。
我们用一个三位数组记录此时的状态。
#构建三个二维列表(9*9)(代码里整合到了一个三维列表里),元素全部初始化为False。
#第一个二维列表的某个位置(i,j),表示第i行是否有数j在,如果有是True,没有是False。
#第二个二维列表的某个位置(i,j),表示第i列是否有数j在,如果有是True,没有是False。
#第三个二维列表的某个位置(i,j),表示第i个box是否有数j在,如果有是True,没有是False。
jugement = [[[False for _ in range(0,9)] for _ in range(0,9)] for _ in range(0,3)]
根据题目提供的数独的初始化状态,由不重复的原则,我们可以从每行中挑选出可以供我们选择的数字组合。顺便将jugement的某些已经在数独中的元素置为True。
choose = [['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9']]
for row in range(9):
for column in range(9):
box_index = int(row/3) * 3 + int(column/3)
if board[row][column] is '.':
location.append((count,row, column))
count += 1
else:
choose[row].remove(board[row][column])
jugement[0][row][int(board[row][column])-1] = True
jugement[1][column][int(board[row][column])-1] = True
jugement[2][box_index][int(board[row][column])-1] = True
如果回溯法的过程中,发现遇到了不合法的数字组合,那么我们要回退到上一个状态去。
判断的函数定义如下:
def isValid(board,position,value):
num = int(value)
row = position[0]
column = position[1]
box_index = int(row/3) * 3 + int(column/3)
if jugement[0][row][num-1] or jugement[1][column][num-1] or jugement[2][box_index][num-1]:
return False
else:
jugement[0][row][num-1] = True
jugement[1][column][num-1] = True
jugement[2][box_index][num-1] = True
return True
回退的方式定义如下:
# 将已经填入到board内的数字重置
board[position[0]][position[1]] = '.'
# 将判断矩阵相应元素重置
jugement[0][position[0]][int(value)-1] = False
jugement[1][position[1]][int(value)-1] = False
jugement[2][box_index][int(value)-1] = False
最后,如果有一种情况能够遍历到最后一个空格位置,那么说明此刻我们的数独的解已经找到了。
6.1.3 完整代码
class Solution:
def solveSudoku(self, board):
location = []
count = 1
jugement = [[[False for _ in range(0,9)] for _ in range(0,9)] for _ in range(0,9)]
choose = [['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9'],
['1', '2', '3', '4', '5', '6', '7', '8', '9']]
for row in range(9):
for column in range(9):
box_index = int(row/3) * 3 + int(column/3)
if board[row][column] is '.':
location.append((count,row, column))
count += 1
else:
choose[row].remove(board[row][column])
jugement[0][row][int(board[row][column])-1] = True
jugement[1][column][int(board[row][column])-1] = True
jugement[2][box_index][int(board[row][column])-1] = True
location.append((count,-1,-1))
def isValid(board,position,value):
num = int(value)
row = position[0]
column = position[1]
box_index = int(row/3) * 3 + int(column/3)
if jugement[0][row][num-1] or jugement[1][column][num-1] or jugement[2][box_index][num-1]:
return False
else:
jugement[0][row][num-1] = True
jugement[1][column][num-1] = True
jugement[2][box_index][num-1] = True
return True
def back(board:list,current_location:tuple):
position = (current_location[1],current_location[2])
next_count = current_location[0]
if position == (-1, -1):
return True
for value in choose[current_location[1]]:
if isValid(board,position,value) is True:
board[position[0]][position[1]] = value
next_positon = location[next_count]
if back(board,next_positon) is True:
return True
else:
box_index = int(position[0]/3) * 3 + int(position[1]/3)
board[position[0]][position[1]] = '.'
jugement[0][position[0]][int(value)-1] = False
jugement[1][position[1]][int(value)-1] = False
jugement[2][box_index][int(value)-1] = False
return False
back(board, location[0])
6.2 N皇后
6.2.1 问题描述
N皇后问题是一个以国际象棋为背景的问题:如何能够在 N×N 的国际象棋棋盘上放置N个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。

6.2.2 问题分析
按行的顺序来依次摆放皇后,但是每摆一枚皇后要注意不能够在已经摆放好的皇后的攻击范围之内,皇后的攻击范围在它所在的行、列,还有主次对角线。那么如何判断当前放置的皇后与其他的皇后是否有冲突呢?
1.因为我们是按行摆放的,所以不用担心在行上皇后能够互相攻击到。
2.用一个一维列表cols[col]表示某列是否有皇后。
3.注意到,对于每一条主对角线,该对角线上的row-column = K(常数)(1-n<=K<=n-1),对于每一条次对角线,该对角线上的row + column = K(常数)(2<=K<=2*n)。
所以我们可以用两个一维列表分别判断主次对角线上是否放置了皇后。
main_diagonals = [0] * (2 * n - 1)
sub_diagonals = [0] * (2 * n - 1)
6.2.3 完整代码
class Solution:
def solveNQueens(self, n: int) -> list:
def could_place(row, col):
return not (cols[col] + main_diagonals[row - col] + sub_diagonals[row + col])
def place_queen(row, col):
queens.add((row, col))
cols[col] = 1
main_diagonals[row - col] = 1
sub_diagonals[row + col] = 1
def remove_queen(row, col):
queens.remove((row, col))
cols[col] = 0
main_diagonals[row - col] = 0
sub_diagonals[row + col] = 0
def add_solution():
solution = []
for _, col in sorted(queens):
solution.append('.' * col + 'Q' + '.' * (n - col - 1))
output.append(solution)
def backtrack(row=0):
for col in range(n):
if could_place(row, col):
place_queen(row, col)
if row + 1 == n:
add_solution()
else:
backtrack(row + 1)
remove_queen(row, col)
cols = [0] * n
main_diagonals = [0] * (2 * n - 1)
sub_diagonals = [0] * (2 * n - 1)
queens = set()
output = []
backtrack()
return output
6.3 迷宫路径
6.3.1 问题描述
输入n * m 的二维数组 表示一个迷宫,数字0表示障碍 1表示能通行,移动到相邻单元格用1步,求解迷宫路径。
6.3.2 问题分析
基本思路是:
每个时刻总有一个当前位置,开始时这个位置是迷宫人口。
如果当前位置就是出口,问题已解决。
否则,如果从当前位置己无路可走,当前的探查失败,回退一步。
取一个可行相邻位置用同样方式探查,如果从那里可以找到通往出口的路径,那么从当前位置到出口的路径也就找到了。
在整个计算开始时,把迷宫的人口(序对)作为检查的当前位置,算法过程就是:
mark当前位置:
检查当前位置是否为出口,如果是则成功结束。
逐个检查当前位置的四邻是否可以通达出口(递归调用自身)。
如果对四邻的探索都失败,报告失败。
6.3.3 完整代码
dirs = [(0, 1), (1, 0), (0, -1), (-1, 0)] # 当前位置四个方向的偏移量
path = [] # 存找到的路径
def mark(maze, pos): # 给迷宫maze的位置pos标"2"表示“到过了”
maze[pos[0]][pos[1]] = 2
def passable(maze, pos): # 检查迷宫maze的位置pos是否可通行
return maze[pos[0]][pos[1]] == 0
def find_path(maze, pos, end):
mark(maze, pos)
if pos == end:
print(pos, end=" ") # 已到达出口,输出这个位置。成功结束
path.append(pos)
return True
for i in range(4): # 否则按四个方向顺序检查
nextp = pos[0] + dirs[i][0], pos[1] + dirs[i][1]
# 考虑下一个可能方向
if passable(maze, nextp): # 不可行的相邻位置不管
if find_path(maze, nextp, end): # 如果从nextp可达出口,输出这个位置,成功结束
print(pos, end=" ")
path.append(pos)
return True
return False
def see_path(maze, path): # 使寻找到的路径可视化
for i, p in enumerate(path):
if i == 0:
maze[p[0]][p[1]] = "E"
elif i == len(path) - 1:
maze[p[0]][p[1]] = "S"
else:
maze[p[0]][p[1]] = 3
print("\n")
for r in maze:
for c in r:
if c == 3:
print('\033[0;31m' + "*" + " " + '\033[0m', end="")
elif c == "S" or c == "E":
print('\033[0;34m' + c + " " + '\033[0m', end="")
elif c == 2:
print('\033[0;32m' + "#" + " " + '\033[0m', end="")
elif c == 1:
print('\033[0;;40m' + " " * 2 + '\033[0m', end="")
else:
print(" " * 2, end="")
print()
if __name__ == '__main__':
maze = [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], \
[1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1], \
[1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1], \
[1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1], \
[1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1], \
[1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1], \
[1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1], \
[1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1], \
[1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1], \
[1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1], \
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1], \
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
start = (1, 1)
end = (10, 12)
find_path(maze, start, end)
see_path(maze, path)
那么如果要求解的是一个最短到达迷宫终点的路径呢?此时,深度优先遍历并不是一个解决这个问题的好算法,因为深度优先遍历只会优先考虑当前解的状态是否合理,对于迷宫而言,如果当前的路是通路,那么它就会继续走下去,直到遇到障碍物或者走到了出口,显然这并不满足我们对最短路径的要求。某种程度上,深度优先遍历更像是一种贪心策略。
解决这个问题的最好方式是广度优先遍历(BFS),大家感兴趣的话可以了解一下广度优先遍历是怎么解决这个问题的,在这里我就不展开了。
7 结论
对于回溯法,上述的例子已经讲解的差不多了,其实分析一个问题如何用回溯法解决,关键部分在于如何高效地判断当前的状态是否合法,如果不合法,果断剪枝。还有就是如果当前的状态不合法,要正确的回溯到前一个状态。
在搜索时,更加高级一点的策略是:针对问题的特点,来制定一个启发式的搜索策略。
8 参考资料
1.Leetcode 46 Permutations
2.Leetcode 47 Permutations II
3.Leetcode 60 Permutation Sequence
4.Leetcode 31 Next Permutation
5.Leetcode 37 Sudoku Solver
6.Leetcode 51 N-Queens