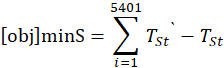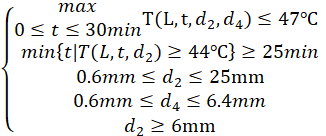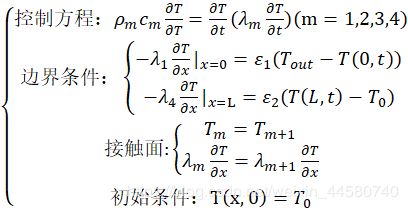数学建模 CUMCM2018年A题真题(原创)
目录
1.问题重述... 3
1.1问题背景... 3
1.2问题提出... 3
1.3本文需要解决的问题... 3
2.模型假设... 3
3.符号说明... 4
4.问题分析... 4
4.1针对问题一... 4
4.2针对问题二... 5
4.3针对问题三... 5
5.模型建立与求解... 5
5.1问题一的模型建立与求解... 5
5.1.1模型的准备... 5
5.1.2数据处理... 6
5.1.3模型建立与求解... 7
5.1.4 敏感性分析... 12
5.2问题二的模型建立与求解... 12
对流换热系数最优解模型... 13
5.2.4模型的结果分析... 14
5.2.5模型二的敏感度分析... 15
5.3问题三的模型建立和求解... 15
5.3.1模型的准备... 15
5.3.2约束条件的确定... 15
5.3.3模型的求解... 16
模型的算法执行... 16
6.评价与改进... 18
6.1模型的优点... 18
6.1.1模型一的优点... 18
6.1.2模型二的优点... 19
6.2.3模型三的优点... 19
6.2模型的缺点... 19
6.2.1模型一的缺点... 19
6.2.2模型二的缺点... 19
6.2.3模型三的缺点... 19
6.3模型的改进... 19
6.3.1对辐射传热的改进... 19
7.参考文献... 21
8.附录... 22
题目 高温作业专用服装设计
摘 要:
本文针对多层材料的高温防护服的传热问题进行研究,综合考虑多种传热方式建立传热模型,以此模型为基础分别解决了一定条件下各层防护材料的温度分别和最佳厚度的问题。
对于问题一,要求在热物性系数不足的情况下求热量分布,故需先求取所缺少的空气对流换热系数。本文首先建立了一维热传导微分方程模型,确定了三个定解条件,随后根据最小二乘法的思想,以左边界空气对流换热系数为决策变量,以可能的空气对流换热系数对应的假人皮肤外侧理论温度与测量温度之差的平方和最小为目标函数,建立基于非线性规划的确定对流换热系数的模型。最后,设计了基于连续变量离散化的二次搜索算法,求解出对流换热系数的最优解。结果显示:空气对流热换系数的最佳值为 ![]() 。同时得出温度分布,数据见 Excel 文件。
。同时得出温度分布,数据见 Excel 文件。
对于问题二,首先在问题一求解的对流换热系数的基础上得到完备的热物性系数, 随后建立单目标问题的优化模型,以服装重量最小为目标函数,以满足题中所给定的隔热效果为约束条件,在给定的第Ⅱ层厚度的范围内进行遍历搜索,绘出不同厚度下的皮肤最外侧温度变化曲线,找到全局最优值。结果显示:第Ⅱ层的最优厚度为 17.6mm。
对于问题三,在问题二的基础上,由探究单一变量扩展为探究多变量。本文对此建 立多目标优化模型,分别以两层材料的总厚度(![]() )最薄和总重量(
)最薄和总重量(![]() )最轻为优化目标,以隔热达到一定效果为约束条件,求取多目标非线性优化模型的最优解。对于多目标问题首先进行降维处理,按不同权重加和形成单目标,从而转变为单目标问题的求解。由于变量的可行解的数量较大,故采用遗传算法搜索全局最优解。结果显示:第Ⅱ 层的最优厚度为 12.1mm,第Ⅳ层的最优厚度为 5.7mm。
)最轻为优化目标,以隔热达到一定效果为约束条件,求取多目标非线性优化模型的最优解。对于多目标问题首先进行降维处理,按不同权重加和形成单目标,从而转变为单目标问题的求解。由于变量的可行解的数量较大,故采用遗传算法搜索全局最优解。结果显示:第Ⅱ 层的最优厚度为 12.1mm,第Ⅳ层的最优厚度为 5.7mm。
关键词:维热传导偏微分方程;对流换热系数;傅里叶定律;牛顿冷却定律;定解条件;二次搜索算法;最小二乘法;遗传算法;离散化;多目标优化
1.问题重述
1.1问题背景
为设计一种防止人们在高温环境下灼伤的防护服,对其研究,一般由三层材料构成,它们各自的参数值(见附件1)导致每一层具有不同的作用。使用者在高温环境工作时,皮肤与衣服之间由于空隙而多了一层空气层(Ⅳ)。本文讨论在一定温度条件下,人体皮肤外侧各层(Ⅰ,Ⅱ,Ⅲ,Ⅳ)的温度分布情况和目标层防护服隔热材料的最佳厚度
1.2问题提出
根据参数值及假人皮肤外侧温度变化求穿防护服时各层的温度分布(情况满足初始条件与交界面条件),在条件(65℃,Ⅳ层5.5mm,工作60min)下,确定Ⅱ层的最佳厚度,在条件(80℃,工作30min)下,确定Ⅱ,Ⅳ层的最优厚度,检验模型是否具有稳定性,重要参数对结果的影响,服装面积矫正系数是否有设置的必要性。
1.3本文需要解决的问题
1.在温度及参数条件(材料密度,比热,热传导率及Ⅰ,Ⅲ层厚度)一致时,建立各层热量传递数学模型,求解90min内Ⅰ~Ⅳ层的温度变化情况及90min时Ⅰ~Ⅳ层的温度分布情况。
2.在Ⅰ,Ⅲ,Ⅳ层厚度一定时,建立优化模型,讨论在一定条件(65℃,工作60min)下,Ⅱ层的最优厚度。
3.在Ⅰ,Ⅲ层厚度一定的情况下,建立双目标优化模型,确定定解条件,设置目标函数并对模型进行灵敏性,稳定性的检验以分析及重要参数对结果的影响。
2.模型假设
1.假设服装制造质量良好,不会因高温损伤以外的情况而损坏。
2.假设实验用假人皮肤在物理,化学性质上与人类皮肤基本相同。
3.假设人皮肤外侧温度超过47℃或超44℃~46℃ 5min以上被鉴定为灼伤。
4.假设外界温度在防护服工作期间的温度变化忽略不计,被防护服吸收的热量会被等量填补。
5.假设同一层抗热层数值方向的温度都可看做作相同,即一层等温层。
6.假设在未进入测试环境前,衣服最外侧与体温保持一致。
7.假设衣服均只由三种材料构成,不含其它成分,且忽略其它成分对结果的影响。
8.假设热对流系数相关性高于0.5。
9.假定对流热换系数变化不大,采用模型一中求得的![]() 当作模型二的左边界空气对流换热系数。
当作模型二的左边界空气对流换热系数。
10.假设热传导忽略辐射传热。
11.假设考虑热对流现象的气层中空气都是均匀流动的。
3.符号说明 |
|
| 符号 |
含义 |
| Tout t ⅆm ρm cm λm εi Tm m q hs,4 hc,1 obj |
外界环境温度 工作时间 Ⅰ,Ⅱ,Ⅲ,Ⅳ厚度(m=1,2,3,4) 抗热材料密度(m=1,2,3,4) 抗热材料比热容(m=1,2,3,4) 热传导率(m=1,2,3,4) 热交换系数 抗热材料各层温度(m=1,2,3,4) 抗热材料代号Ⅰ,Ⅱ,Ⅲ,Ⅳ 热流密度 皮肤与第Ⅳ层的热对流系数 高温空气与第Ⅰ层材料的热对流系数 目标函数 |
4.问题分析
4.1针对问题一
对于问题一,需要通过研究分析附件1和附录2,热量在各层材料间的传导,得到一定时间内步长范围内的温度分布,对问题二,问题三有意义的结论。
首先,模型准备工作:
1、需要理解附件1的专有名词的物理含义和数值的实际意义;
2、需要理解热量在物质间的传导原理与过程;
3、需要理解定值参数与实际变量。
其次,根据热量传递的过程建立一维热传导偏微分方程模型;确定定解条件(初始条件、边界条件、交界面条件)。
然后,考虑非稳态向稳态转移模型的建立,求解不同物质间的热交换系数(具体含义见下文);得传递时热量的损失。
最后,得到一定时间步长范围内的温度分布,对问题二,问题三有意义的结论。
4.2针对问题二
问题二要求确定II层的最优厚度,使之在特定条件下的隔热能力满足一定要求,显而易见,这是一个具有约束条件的优化问题。在问题一的基础上,假定对流热换系数变化不大,即采用模型一中求得的hc,1 当作模型二的左边界空气对流换热系数,从而得到了完备的热物性系数,进而得出相应的温度分布。从人穿戴舒适度角度考虑,以服装的重量最轻为目标函数,即第 II 层厚度最小;以工作60分钟时,假人皮肤外侧温度不超过 47ºC,且超过 44ºC 的时间不超过5分钟为约束条件建立优化模型。
4.3针对问题三
问题三要求确定第II层和第IV层的最优厚度,并且在特定温度条件下满足一定隔热效果。问题三是在问题二的基础上,由探究单一变量扩展为探究多变量的优化问题。
对此,建立多目标优化模型,分别以两层材料的总厚度(H)最薄和总重量(M)最轻为优化目标,以在特定温度条件下隔热达到一定效果为约束条件,求取非线性优化函数的最优解。
对于多目标优化问题难以直接求解,故将两个目标分别赋予不同权重进行加和,从而将其降维成单目标问题,使之简化成为单目标问题的求解。
5.模型建立与求解
5.1问题一的模型建立与求解
5.1.1模型的准备
防护服是凭借多层高抗热性材料对外界高温产生有效隔离的特种服装(材料Ⅰ,Ⅱ,Ⅲ)。本文研究的是考虑了穿着者与衣服间隙层Ⅳ后,特定外界温度下各层的温度分布。
附录一中的专有名词概念解释如下所示:
表5-1-1 热传导专有名词解释
|
|
|
| 名词概念 |
名词解释 |
| 抗热材料密度 抗热材料比热容 热传导率 热交换系数 |
单位体积材料的质量 单位质量材料的热容量 同种材料传热的能力 异种材料间传热的能力 |
因为热量从外界传递至皮肤需要穿过防护服和间隙,为方便研究,分别对三层材料与间隙编号为Ⅰ,Ⅱ,Ⅲ,Ⅳ。
相关传热规律——傅里叶定律
在各向同性的连续介质中,任意一个时间 t,任何位置的局部导热热流密度方向与该点的温度变化方向(梯度方向)相反,其数值均与该点的温度梯度成正比[2]。热流密度的计算方法如下:
其中,q为热对流密度,n为方向向量,T为物体当前温度(K)。
由上述公式可知,热流q的传递方向与梯度方向相反。
发生热流换热时,热流的计算是通过牛顿冷却定律:
当流体温度比物体低时:![]() (2)
(2)
当流体温度比物体高时:![]() (3)
(3)
其中,![]() 是流体温度,
是流体温度, ![]() 为对流表面温度,是对流换热系数。
为对流表面温度,是对流换热系数。
5.1.2数据处理
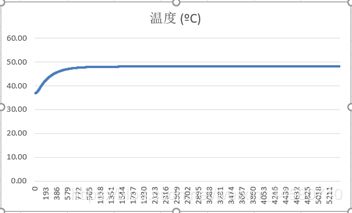
在条件一定的情况下,在实验环境测得附件二中数据,可绘制出随皮肤外温度(T)随时间(t)变化的曲线,如图所示:
图5-1-2 皮肤外温度(T)随时间(t)变化的曲线
5.1.3模型建立与求解
为了研究问题一,建立了两个数学模型:
1.一维热传导偏微分方程模型
- 热传导方程概述
热传导方程是一个重要的偏微分方程,它描述一个区域内的温度如何随时间变化。在一维环境下,特定点的温度会因步长和时间的改变而改变,为得到求得方程的有效数值解,必须限制定解条件[1]。
现将“高温环境-服装-空气层-皮肤”系统简化为如下图所示:
图5-1-3 热传递步长简化图
![]()
其中,x表示防护服内各点到第Ⅰ层最外侧的距离,
d表示防护服的厚度;
![]() 表示总工作时间;
表示总工作时间;
比热容C,密度![]() 和热传导率
和热传导率![]() 均为常数。
均为常数。
表5-1-3 物质导热系数的数量级
说明![]() ,热量在气体中的传播效率最低。
,热量在气体中的传播效率最低。
- 定解条件的计算与分析
为了得到各层的温度分布情况,还需求出偏微分方程的定解条件;
(i)边界条件:本模型的边界条件并不是固定不变的,经分析,他满足第三类洛平(Robin)条件,故
![]() (5)
(5)
根据文献[3],
![]()
带入知:
同样得到右边值:
(ii)初始条件
由假设7,8可知初始时在特定温度的环境里,皮肤外侧满足
![]() (8)
(8)
其中![]() ,为假设初始时的皮肤外侧温度。
,为假设初始时的皮肤外侧温度。
(iii)连续性条件(交界面条件)
由于防护服有多层,在相邻两层接触面处满足温度和热流密度连续。由《热传导理论》可知温度与热流密度连续是交界面连续的充要条件,即:
Tm-=Tm+|x=d=T0,m=1,2,3![]() (9)
(9)
其中,Tm![]() 表示第m层与第m+1层接触面lm
表示第m层与第m+1层接触面lm![]() 处的温度;
处的温度;
qm![]() 表示lm
表示lm![]() 处的热流密度;
处的热流密度;
上式的上标“-”、“+”分别表示左右极限。
综上所述,建立数学模型如下
问题的求解步骤如下图所示
图5-1-4 求解流程图
边界条件依赖于假人皮肤外侧温度T,而T一般需要测量得到,在一定条件下,75℃,![]() ,
, ![]() ,工作90min的情况下可由Robin条件确定此时的热交换系数。
,工作90min的情况下可由Robin条件确定此时的热交换系数。
2.稳定性离散模型
(i)解析解的确定
由于以上问题均为偏微分方程问题,且其没有解析解,只有数值解,故对其时间进行离散,取空间步长h=0.05mm,时间步长k=1s,得(M+1)×(N+1)个点构成的离散网络,其中:N=![]() ,M=,
,M=,![]() ,为确保数值求解稳定且收敛,我们考虑使用隐式差分法,代码见附录3:
,为确保数值求解稳定且收敛,我们考虑使用隐式差分法,代码见附录3:
对模型1进行离散化处理形成:
![]()
![]()
其中,![]() 表示第n层的热传导率;
表示第n层的热传导率;
![]() (14)
(14)
将式(14)与式(11),(13)联立,可由Tj![]() 时刻温度
时刻温度![]() 递推得到
递推得到![]() 时刻温度
时刻温度![]() ;
;
该递推式为一个三对角线性方程组。
(ii)目标函数的确定
基于最小二乘法的思想,本模型的目标为:可能的对流换热系数![]() 对应的每个时刻的假人皮肤外侧温度与测量温度之差的平方和最小。
对应的每个时刻的假人皮肤外侧温度与测量温度之差的平方和最小。
分别以 ![]() 表示第 i 个时刻假人皮肤外侧的测量温度,以
表示第 i 个时刻假人皮肤外侧的测量温度,以![]() 表示第 t 个时刻假人皮肤外侧的计算温度,故目标函数为:
表示第 t 个时刻假人皮肤外侧的计算温度,故目标函数为:
将其与实测皮肤外侧温度(图5-1-2)进行比较,
图5-1-5 曲线比较图
这两条曲线吻合较好,偏离数值差仅为0.2546<<1,故选取的参数是合理的。
(iii)模型的最后求解
综上所述,本文建立确定对流换热系数模型如下:
![]() (16)
(16)
参考图5-1-3可知,在Ⅰ,Ⅱ,Ⅲ,Ⅳ层中考虑热导率,在a,b,c处考虑热交换系数。
由模型1可计算出在工作时间[0,tm![]() ]内某时刻某层的温度情况,分别以步长h为x轴,时间为t轴,温度为T轴建立坐标系用MATLB绘制出温度分布图,程序源码及完整结果见附件3。
]内某时刻某层的温度情况,分别以步长h为x轴,时间为t轴,温度为T轴建立坐标系用MATLB绘制出温度分布图,程序源码及完整结果见附件3。
结果显示:左边界空气对流传热系数值为 ![]() m×s ,温度分布数据保存为 Excel 文件(文件名为 problem1.xlsx).
m×s ,温度分布数据保存为 Excel 文件(文件名为 problem1.xlsx).
图5-1-4 温度分布图
![]()
由图可看出随x的增加,温度呈递减趋势,随时间递增,热传导由非稳态变为稳态,即在一定时间后各位置温度变为一个恒定值,从防护服外侧到假人体表外侧,温度呈递减趋势,并且减小的速率与各层参数有关,符合实际情况。
随时间的增加,各层温度有所上升,最终在![]() 时趋于稳态,达到Ⅳ层的
时趋于稳态,达到Ⅳ层的![]() 。
。
图5-1-5 温度随厚度的变化曲线
3.模型计算的验证
参考附件二及图5-1-2曲线也满足上述结论,最终在5400s时趋于稳态。
5.1.4 敏感性分析
![]() 的结果受
的结果受![]() ,
,![]() ,
,![]() ,
, ![]() 的影响,而在实际中这些因素的取值不能保证准确无误,因此需要分别分析当这些因素发生轻微改变时会对结果产生怎样的影响,从而得到模型的敏感性。
的影响,而在实际中这些因素的取值不能保证准确无误,因此需要分别分析当这些因素发生轻微改变时会对结果产生怎样的影响,从而得到模型的敏感性。
其他条件不变,外侧空气热对流系数随皮肤侧空气热对流系数的变化如下表:
表5.1.4 外侧空气热对流系数随皮肤侧空气热对流系数的变化
通过表格的数据可知,右边界空气的对流换热系数改变时,左边界空气的对流换热系数不会发生较大变化;同样地,分别在只改变密度、比热、导热系数的情况下进行检验,发现左边界空气的对流换热系数基本稳定在![]() m×s 左右。因此可以得出结论: 该模型的稳定性良好。
m×s 左右。因此可以得出结论: 该模型的稳定性良好。
5.2问题二的模型建立与求解
5.2.1模型的准备
问题二要求确定II层的最优厚度,使之在特定温度条件下的隔热能力满足一定要求,显而易见,这是一个具有明确约束条件的优化问题。从人穿戴舒适度角度考虑,以服装的重量最轻为优化目标,结合约束条件建立简易的优化模型即可。
对流换热系数最优解模型
(i)变量的确定
综合前文的分析,本模型的热物性系数已经完备,不需再进行求解,因此决策变量只有第II层的厚度ⅆ2 。
(ii)目标函数的确定
从人体穿戴舒适度角度来讲,重量越轻的服装穿戴的舒适性越高。在服装展开总面积一定的情况下,重量与厚度成正比,因此目标函数转化成为第II层材料厚度最小。
![]() (18)
(18)
(iii)约束条件的确定
题目要求在环境温度为 65ºC,确保工作60分钟时,假人皮肤外侧温度不超过 47ºC,且超过 44ºC 的时间不超过5分钟。因为在传热过程中皮肤外表面温度是不断上升的,因此可以转化为便于计算的约束条件:
附件1专用服装材料的参数值给定了第 II 层材料厚度d2![]() 的范围,即
的范围,即
![]() (20)
(20)
5.2.2最终模型的确立
综上所述,本文建立确定对流换热系数模型如下
5.2.3模型的求解与结果
(i)求解算法
通过分析,认为所求![]() 精度为0.1mm,而
精度为0.1mm,而![]() 范围较小,该范围内的可行解的个数少于250个,因此可用遍历搜索法求全局最优解。
范围较小,该范围内的可行解的个数少于250个,因此可用遍历搜索法求全局最优解。
(ii)求解结果
运用Matlab进行求解运算,程序源码及运行结果见附录4;
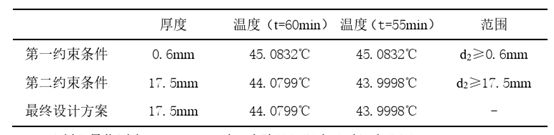
由边界条件计算算法可得边界条件临界值如下表所示:
表5-2-3 约束条件临界值
绘制出最优厚度![]() 时,皮肤外侧温度随时间的变化曲线,
时,皮肤外侧温度随时间的变化曲线,
图5-2-3 ![]() ,皮肤外侧温度随时间的变化曲线
,皮肤外侧温度随时间的变化曲线
结果显示,第Ⅱ层材料的最佳厚度为17.5mm,在t=55min时,皮肤表面温度为43.9998℃,接近于临界温度44℃,最高温度为44℃,满足约束条件。
由于傅里叶网格条件的限制以及离散数值求解的精度限制,为确保不出现解的震荡和精度损失,求解精度仅能精确到0.1mm。
下图绘制出不同材料厚度下,皮肤外层温度与时间数值关系;
图5-2-4 不同![]() 厚度T-t关系
厚度T-t关系
5.2.4模型的结果分析
根据问题一的稳态防护服温度分布图5-1-4,可见第二层温度梯度最小,两端温差最小,第二层厚度的变化对最大温度的影响占次要因素,第二层主要起延缓传热过程等其他作用,且温度始终低于47℃是合理的。
5.2.5模型二的敏感度分析
第Ⅱ层材料的最佳厚度![]() 的结果受 1
的结果受 1![]() ,hs,
,hs,![]() ,Ki
,Ki![]() , Ci
, Ci![]() , ri
, ri![]() 的影响,而在实际中这些因素的取值无法准确无误,因此需要分别分析当这些因素发生轻微改变时会对结果产生怎样的影响,从而得到模型的敏感性。
的影响,而在实际中这些因素的取值无法准确无误,因此需要分别分析当这些因素发生轻微改变时会对结果产生怎样的影响,从而得到模型的敏感性。
分别在只改变 hc,1![]() ,4
,4![]() ,
,![]() ,
, ![]() , i
, i![]() 的情况下进行检验,发现
的情况下进行检验,发现![]() 变化不是太大,因此可以得出结论:该模型的稳定性良好。
变化不是太大,因此可以得出结论:该模型的稳定性良好。
5.3问题三的模型建立和求解
5.3.1模型的准备
问题三增加了第四层厚度的设计,为降低研发成本,节省时间,就要考虑服装制作成本,防护服笨重程度,舒适度。同时考虑最高温度,高温时间和厚度作为约束条件,建立多目标优化模型。
1.优化目标
(i)舒适性目标:
隔热效果相同时衣服厚度最小,防护服灵活性高 ,便于穿着作业。
(ii)节约性目标:
第四层为空气层,不消耗成本,所以第二层厚度近可能小。
(iii)性能稳定性目标:
第二层导热率最大,对热辐射的隔热性能最好,故第二层不能太薄。第四层为空气层,若过厚会造成厚度分布不均匀,引起灼伤,故不能太厚。
(iiii)研发效率目标:
为缩短研发周期,应尽可能减少实验次数,故该防护服应用范围应该广泛。
所以优化目标为
且![]() (25)
(25)
5.3.2约束条件的确定
记函数T(x,t, d2![]() , d4
, d4![]() )为第二层厚度为
)为第二层厚度为![]() ,第四层厚度为
,第四层厚度为![]() 时的温度分布函数。
时的温度分布函数。
由题意:皮肤外侧温度不超过47![]() 超过44℃
超过44℃![]() 时间不超过5分钟。
时间不超过5分钟。
5.3.3模型的求解
上述双目标模型难以直接求解,因此需要通过降维的方式,将双目标问题转化为单目标,降维步骤如下:
STEP1.分别计算不同的情况下的 H 和 M 的值;
STEP2.将 H 和 M 分别进行标准化得到各自对应的标准化值 ![]() 和
和 ![]() ; STEP3.将标准化后的值分别赋予不同权重 p 和 1- p 相加,
; STEP3.将标准化后的值分别赋予不同权重 p 和 1- p 相加,
形成单目标函数
![]() (27)
(27)
最终模型的确立
![]() (28)
(28)
5.3.4模型的算法执行
由于可行解数量比较大,故运用遗传算法进行求解.遗传算法求解具体步骤如下:
STEP1:产生随机染色体:随机产生 50 组初始染色体,作为初始值,分别求出 对应的适应度函数;
STEP2:编码:将 50 组群体转化为二进制编码;
STEP3:迭代次数 ![]() ,
,![]() ;
;
STEP4:交叉:产生随机数,将编码后的 50 ![]() 组染色体两两交换其染色体上随机 对应序列号的编码值,并生成子代;
组染色体两两交换其染色体上随机 对应序列号的编码值,并生成子代;
STEP4:变异:产生随机数,取变异概率为 0.1,将交叉后的 50 组染色体的对应 序列号的而进制编码变异,即 0 变为 1,1 变为 0,并生成变异子代;
STEP5:求出所有父代,子代以及变异子代的十进制数值;
STEP6:求出所有父代,子代,以及变异子代对应的适应度函数,筛选出其中最 s.t. 15 小的 50 组作为新的父代。若迭代次数达到最大迭代次数,进入 STEP7,否则,返回 STEP3;
STEP7:从最终迭代完成后的数据组里面选出最小的一组作为最优解.
- 由于优化目标为在尽可能减少成本的前提下再缩短研发周期。反映到题目中就是第四层材料导热系数远小于第二层材料,故在外界环境相同时,第四层越厚,隔热效果越好,且成本最小。
所以,在 时,求第二层的最小厚度。
时,求第二层的最小厚度。
图5-3-3 固定厚度d2![]() 的T-t图
的T-t图
图5-3-4固定d4![]() 的T-t图
的T-t图
(2)在模型二的前提下,用相同的解法,得到最优厚度。
d2=19.3mm, d4=6.4mm![]()
5.3.5敏感性分析
第Ⅱ层材料的最佳厚度d2![]() 和第Ⅳ层材料的最佳厚度
和第Ⅳ层材料的最佳厚度 ![]() 的结果受 hc,1
的结果受 hc,1![]() ,hs,4
,hs,4![]() ,Ki
,Ki![]() , Ci
, Ci![]() , ri
, ri![]() 的影响,分别在只改变 hc,1
的影响,分别在只改变 hc,1![]() ,hs,4
,hs,4![]() ,Ki
,Ki![]() , Ci
, Ci![]() , ri
, ri![]() 的情况下进行检验,发现d2
的情况下进行检验,发现d2![]() 和d4
和d4![]() 变化不是太大,因此可以得出结论:该模型的稳定性良好。
变化不是太大,因此可以得出结论:该模型的稳定性良好。
6.评价与改进
6.1模型的优点
6.1.1模型一的优点
1.建立了一维坐标系简明的研究了防护服各层的热传导过程,使研究直观上具有了连续性。
2.充分考虑了热流密度q,考虑过对流对传热的影响,使结果更准确。
3.先绘制出附件2中实际数据的变化图线5-1-2,然后计算在一定条件下,皮肤外侧温度T随时间t的变化的预测图线,将之与5-1-2比较,以拟合度判断结果准确度。
4.运用离散模型确定解析解,将范围网格化,结果稳定且收敛。
5.进行了敏感性分析,验证了各参数变化对于结果的影响。
6.1.2模型二的优点
1.模型求解变量明确,以d2 为单变量。
2.步长设置科学,以0.1mm为精度。
3.考虑全面,使得成本最低(厚度最薄),时间周期最短(实验次数最少)。
4.进行了敏感性分析,验证了各参数变化对于结果的影响。
6.2.3模型三的优点
1.考虑较充分,验证了各个步长厚度范围内的温度变化。
2.设置了科学的定解条件,求解出精度较高的左右边界条件。
3.运用了迭代次数较高,精度较高的遗传算法计算d。
4.将双向变量方程稳态化,转化为单变量问题,分别固定d1和d2 研究各层厚度,给出直观曲线图。
5. 进行了敏感性分析,验证了各参数变化对于结果的影响。
6.2模型的缺点
6.2.1模型一的缺点
1.未考虑热辐射对温度分布的影响,我们在模型的改进里给出了补充研究。
2.每层材料之间都会存在微小间隙,从而使实验值和真实值存在误差。
6.2.2模型二的缺点
工作时长内定解条件的边界条件未给出全局解。
3.空气的热对流系数及材料的导热率会随温度升高而小范围变大,本文未考虑此参数变化。
6.2.3模型三的缺点
所给单变量研究步长对象较大,可能不够精确。
6.3模型的改进
6.3.1对辐射传热的改进
基本假设部分已经假设忽略辐射传热,此时对假设进行检验,并进一步扩展非稳态传热模型,建立考虑辐射传热项的模型,并对模型进行分析。
对于皮肤,可近似考虑为绝对黑体,令![]() ,对于防护服来说,发射率:
,对于防护服来说,发射率:![]() ,由式
,由式
得辐射传热量,其中
![]() 分别为第三层右边界温度和皮肤外侧温度。
分别为第三层右边界温度和皮肤外侧温度。
带入非稳态传热模型中:
其控制方程的离散格式为:
同样的步骤建立换热系数![]() 与实测温度值的数值关系,最佳拟合时结果如下:
与实测温度值的数值关系,最佳拟合时结果如下:
图6-3-1 考虑辐射传热的拟合图像
此时同样可达到较好拟合,与不考虑辐射传热相比,传热系数ε1![]() 保持不变,
保持不变,![]() 由8.344
由8.344![]() 变化为8.496
变化为8.496![]() ,仅有微小变化修正。
,仅有微小变化修正。
表6-3-1 考虑辐射的拟合情况
7.参考文献
[1]《热传导理论》 胡汉平 编;出 版 社: 中国科学技术大学出版社;ISBN: 9787312025815;出版时间: 2010-01-01
[2] 杨世铭,陶文铨.传热学第三版[M].哈尔滨:哈尔滨工业大学硕士学位论文,2015: 20-58
[3] CHITRPHIROMSRI P,KUZNETSOV A V. Modeling heat and moisture transport in firefighter protective clothing during flash fire exposure[J]. Heat and Mass Transfer,2005,41( 3) : 206 - 215.
[4]唐建民,郑志军,人体皮肤和黑体【j】,大学物理,1990(01);46-49
[5]潘斌,热防护服装热传递数学建模及参数决定反问题[D],浙江理工大学,2017.
[6] 程蕾.被测目标热参数反演算法研究[D].哈尔滨:哈尔滨工业大学硕士学位论文, 2015:20-58.
[7] 薛毅.数学建模基础.科学出版社,2011,4
[8] CHITRPHIROMSRI P,KUZNETSOV A V. Modeling heat and moisture transport in firefighter protective clothing during flash fire exposure[J]. Heat and Mass Transfer,2005,41( 3) : 206 - 215.
[9] 李立康 於崇华 朱政华. 微分方程数值解法 [M]. 上海: 复旦大学出版社 1999: 183-218
[10] 全国大学生数学建模竞赛组委会. 2018年高教社杯全国大学生数学建模竞赛赛题[EB/OL].[2019 ̄01 ̄12].http://www.mcm. edu.cn/html_cn/node/7cec7725b9a0ea07b4dfd175e8042c33.html.
[11] 葛新石叶宏. 传热和传质基本原理 [M]. 北京: 化学工业出版社 2007: 58-71.
[12] 卢琳珍徐定华徐映红. 应用三层热防护服热传递改进模型的皮肤烧伤度预测 [J]. 纺织学报 2018ꎬ39 (1): 111- 118-125.
8.附录
附录1:
附录2:
clc,clear;
time=xlsread('问题1各层材料系数.xlsx','sheet2','B3:B5403');
zhong_size=50; %种群数量
d=10; %进化代数
zhang_length=10; %染色体长度
jx=0.8; %交叉概率 by=0.001; %变异概率
zhong=initzhong(zhong_size,zhang_length); %随机生成初始染色体
for i=1:d
b=bianyi(zhong,by); %变异
if ~isempty(b)
newzhong=[zhong;crosspop(zhong,jx);b]; %生成的新种群
else
newzhong=[zhong;crosspop(zhong,jx)];
end [newobject,v]=best(newzhong,time); %求适应值
[object,sod]=sort(newobject);
zhong=newzhong(1:50,:); %选出下一代种群
end
disp('最小的热对流系数:');
vpa(v,6)
%适应度函数 best.m function [object,mn]=best(newzhong,time)
%适应性函数 lana=118;
[d,w]=size(newzhong);
T0=75; T1=37; rho=[300 862 74.2 1.18]; %各层密度
c=[1377 2100 1726 1005]; %比热容
K=[0.082, 0.37, 0.045, 0.028]; %导热系数
a=K./(c.*rho)*10^8;
gg=binary2decimal(newzhong);
H=[6 60 36 50]; %各层厚度
s=zeros(d,1);
x0=0; xf=sum(H); %厚度
t0=0; tf=5400; %时间
mul=1; tau=1;
h=1/mul; 18
M=(xf-x0)/h; %x分为M等分
N=(tf-t0)/tau; %
u=zeros(M+1,N+1);
r=a.*tau/h^2; x=x0:h:
xf; %步长
t=t0:tau:tf; first(1:H(1)-2)=-r(1); %追赶法求解的第一列系数
first(H(1)-1)=-K(1);
first(H(1):H(1)+H(2)-2)=-r(2);
first(H(1)+H(2)-1)=-K(2);
first(H(1)+H(2):H(1)+H(2)+H(3)-2)=-r(3);
first(H(1)+H(2)+H(3)-1)=-K(3);
first(H(1)+H(2)+H(3):H(1)+H(2)+H(3)+H(4)-2)=-r(4);
third(1:H(1)-1)=-r(1); %第三列系数
third(H(1))=-K(2);
third(H(1)+1:H(1)+H(2)-1)=-r(2);
third(H(1)+H(2))=-K(3);
third(H(1)+H(2)+1:H(1)+H(2)+H(3)-1)=-r(3);
third(H(1)+H(2)+H(3))=-K(4);
third(H(1)+H(2)+H(3)+1:H(1)+H(2)+H(3)+H(4)-2)=-r(4);
seconf(1:H(1)-1)=1+2*r(1); %第三列系数
seconf(H(1))=K(1)+K(2);
seconf(H(1)+1:H(1)+H(2)-1)=1+2*r(2);
seconf(H(1)+H(2))=K(2)+K(3);
seconf(H(1)+H(2)+1:H(1)+H(2)+H(3)-1)=1+2*r(3);
seconf(H(1)+H(2)+H(3))=K(3)+K(4); seconf(H(1)+H(2)+H(3)+1:H(1)+H(2)+H(3)+H(4)-1)=1+2*r(4);
%%
%利用第二类边界条件求得矩阵
for all=1:d
u=zeros(M+1,N+1);
lanb=gg(all);
first=[0,first,-2*r(4)];
third=[-2*r(1),third,0]; seconf=[1+2*r(1)-2*r(1)*h*lana/(-K(1)),seconf,1+2*r(4)+2*r(4)*h*lanb/(-K(4) )]; u(1:H(1),1)=37; %初值
u(1+H(1):H(1)+H(2),1)=37;
u(H(1)+H(2)+1:H(1)+H(2)+H(3),1)=37;
u(H(1)+H(2)+H(3)+1:H(1)+H(2)+H(3)+H(4),1)=37;
for j=1:N+1 %边值 19 u(1,j)=T0;
u(M+1,j)=T1; end %% 环境皮肤之间考虑热传导
%%
for j=2:N+1 %向后差分法求数值解
last=[u(2,j-1)+r(1)*u(1,j);u(3:M-1,j-1); u(M,j-1)+r(4)*u(M+1,j)]; last(H(1))=0; last(H(1)+H(2))=0; last(H(1)+H(2)+H(3))=0; last=[u(1,j-1)-T0*2*r(1)*h*lana/(-K(1));last;u(M+1,j-1)+2*r(4)*h*T1*lanb/(- K(4))]; A=tridiag(first,seconf,third,last); %追赶法求解
u(1:M+1,j)=A;
end
v=u(H(1)+H(2)+H(3)+H(4),:);
for m=1:5401
s(all)=s(all)+(v(m)-time(m))^2; %求得平方差
end s(all)=s(all)/length(v);
end
object=s; %适应度值
mn=lana;
%mn=gg-0.0000805;
%遗传算法初始化种群 initzhong.m
function A=initzhong(size,length)
%初始化种群
A=round(rand(size,length));
Return
%遗传算法二进制转十进制 binary2decimal.m
function pop2 = binary2decimal(pop)
%将二进制转换为数值
[px,py]=size(pop);
for i = 1:py
pop1(:,i) = 2.^(py-i).*pop(:,i);
end
%sum(.,2)对行求和,得到列向量
temp = sum(pop1,2);
pop2 = 0.02400+0.00300*temp/(2^10-1);
shading interp;
附录3:
clc,clear; T0=65; T1=37; lana=118; %左侧的热对流系数
lanb = 0.0263506; %右边界热对流系数
rho=[300 862 74.2 1.18]; %各层密度
c=[1377 2100 1726 1005]; %比热容
K=[0.082, 0.37, 0.045, 0.028]; %导热系数
a=K./(c.*rho)*10^8; weight=0.6:0.1:25; %厚度范围
count=0; for z=1:length(weight) L=[6 round(weight(z)*10) 36 55]; %各层厚度 % L=[6];
x0=0; xf=sum(L); %厚度
t0=0; tf=3600; %时间
mul=1; tau=1; h=1/mul;
M=(xf-x0)/h; %x分为M等分
N=(tf-t0)/tau; % u=zeros(M+1,N+1);
r=a.*tau/h^2;
x=x0:h:xf;
t=t0:tau:tf;
u(1:L(1),1)=37; %初值
u(1+L(1):L(1)+L(2),1)=37;
u(L(1)+L(2)+1:L(1)+L(2)+L(3),1)=37;
u(L(1)+L(2)+L(3)+1:L(1)+L(2)+L(3)+L(4),1)=37; for j=1:N+1 %边值
u(1,j)=T0; u(M+1,j)=37;
end %追赶法求解的第一列
aa(1:L(1)-2)=-r(1);
aa(L(1)-1)=-K(1);
aa(L(1):L(1)+L(2)-2)=-r(2);
aa(L(1)+L(2)-1)=-K(2);
aa(L(1)+L(2):L(1)+L(2)+L(3)-2)=-r(3);
aa(L(1)+L(2)+L(3)-1)=-K(3);
24
aa(L(1)+L(2)+L(3):L(1)+L(2)+L(3)+L(4)-2)=-r(4); %追赶法求解的第三列
cc(1:L(1)-1)=-r(1);
cc(L(1))=-K(2);
cc(L(1)+1:L(1)+L(2)-1)=-r(2);
cc(L(1)+L(2))=-K(3);
cc(L(1)+L(2)+1:L(1)+L(2)+L(3)-1)=-r(3);
cc(L(1)+L(2)+L(3))=-K(4);
cc(L(1)+L(2)+L(3)+1:L(1)+L(2)+L(3)+L(4)-2)=-r(4); %追赶法求解的第二列
bb(1:L(1)-1)=1+2*r(1);
bb(L(1))=K(1)+K(2);
bb(L(1)+1:L(1)+L(2)-1)=1+2*r(2);
bb(L(1)+L(2))=K(2)+K(3);
bb(L(1)+L(2)+1:L(1)+L(2)+L(3)-1)=1+2*r(3);
bb(L(1)+L(2)+L(3))=K(3)+K(4);
bb(L(1)+L(2)+L(3)+1:L(1)+L(2)+L(3)+L(4)-1)=1+2*r(4);
aa=[0,aa,-2*r(4)];
cc=[-2*r(1),cc,0];
bb=[1+2*r(1)-2*r(1)*h*lana/(-K(1)),bb,1+2*r(4)+2*r(4)*h*lanb/(-K(4))];
for j=2:N+1 %向前差分法求数值解 % u(1,j+1) % aa(1:M-2)=-r; % cc=aa; %
bb(1:M-1)=1+2*r;
dd=[u(2,j-1)+r(1)*u(1,j);u(3:M-1,j-1);
u(M,j-1)+r(4)*u(M+1,j)];
dd(L(1))=0;
dd(L(1)+L(2))=0;
dd(L(1)+L(2)+L(3))=0;
dd=[u(1,j-1)-T0*2*r(1)*h*lana/(-K(1));dd;u(M+1,j-1)+2*r(4)*h*T1*lanb/(-K(4) )]; A=tridiag(aa,bb,cc,dd);
u(1:M+1,j)=A; % u(1:M+1,j)=A; end v=u(M+1,:);
if max(v)<=47 %约束条件,判断是否符合条件
if length(find(v>=44))<=300 count=count+1;
fitweight(count)=weight(z); %记录符合条件的值
end 25 end end disp('最优的厚度为:');
fitweight(1)