后缀自动机SAM题目总结
Hihocoder我的入门SAM
后缀自动机一·基本概念
题意
从零开始学习SAM入门,讲的非常好
思路
仔细阅读题目理解SAM各种性质
我的入门代码
后缀自动机二·重复旋律5(入门题)
题意
求整个串中本质不同子串个数(本质不同:两个串的长度或内容有差异)
∣ S ∣ ≤ 1 0 5 |S|\le 10^5 ∣S∣≤105
思路
对原串构造SAM, a n s = ∑ i ∈ [ 1 , c n t ] m x l [ i ] − m x l [ p r e [ i ] ] ans=\sum_{i\in [1,cnt]}mxl[i]-mxl[pre[i]] ans=∑i∈[1,cnt]mxl[i]−mxl[pre[i]]
代码在这里
后缀自动机三·重复旋律6
题意
求出所有长度为 K ∈ [ 1 , ∣ S ∣ ] K\in [1,|S|] K∈[1,∣S∣] 的子串的最大出现次数
∣ S ∣ ≤ 1 0 5 |S|\le 10^5 ∣S∣≤105
思路
先用基数排序计算出每个节点的 ∣ e n d p o s ( s ) ∣ |endpos(s)| ∣endpos(s)∣ 即该点的endpos集合大小,如果对于他所管辖的串个数 [ m x l [ p r e [ i ] ] + 1 , m x l [ i ] ] [mxl[pre[i]]+1,mxl[i]] [mxl[pre[i]]+1,mxl[i]] 都去更新的话,复杂度会退化为 O ( n 2 ) O(n^2) O(n2) ,发现 a n s [ 1 ] , a n s [ 2 ] , a n s [ 3 ] . . . a n s [ n ] ans[1],ans[2],ans[3]...ans[n] ans[1],ans[2],ans[3]...ans[n] 一定是单调递减的序列,所以我们只需要更新他所管辖的长度中的最大值即可,最后再从大到小更新答案,如果 a n s [ i ] < a n s [ j ] 且 i < j ans[i]<ans[j] 且 i<j ans[i]<ans[j]且i<j 更新 a n s [ i ] = a n s [ j ] ans[i]=ans[j] ans[i]=ans[j]
代码在这里
后缀自动机四·重复旋律7
题意
给出 N N N 个只由 [ 0 , 9 ] [0,9] [0,9] 组成的字符串 S S S ,求所有本质不同的子串"和"(把串看成数字,在十进制下求和,允许有前导0)
∑ ∣ S ∣ ≤ 1 0 5 \sum|S|\le 10^5 ∑∣S∣≤105
思路
首先看到多个串处理,可以用广义SAM处理他们本质不同的子串,方法:每次新插入一个串时,last=1,Extend时注意判断 c h [ p ] [ c ] ch[p][c] ch[p][c] 是否有值,如果有则 l a s t = c h [ p ] [ c ] last=ch[p][c] last=ch[p][c] 直接返回,否则和普通SAM一样.
再用基数排序(注意:基数排序在广义SAM中必须保证没有多余的节点,即Extend一定要特判才能使用),发现每个节点的sum[v]可以由 c h [ u ] [ c ] = v ch[u][c]=v ch[u][c]=v 的u节点的sum[u]过来,有 s u m [ v ] = ∑ c h [ u ] [ c ] = v s u m [ u ] ∗ 10 + c ∗ ( m x l [ u ] − m x l [ p r e [ u ] ] ) sum[v]=\sum_{ch[u][c]=v}{sum[u]*10+c*(mxl[u]-mxl[pre[u]])} sum[v]=∑ch[u][c]=vsum[u]∗10+c∗(mxl[u]−mxl[pre[u]]), m x l [ u ] − m x l [ p r e [ u ] ] mxl[u]-mxl[pre[u]] mxl[u]−mxl[pre[u]] 表示u所管辖的串个数,他们都可以通过c这个字符转移到v节点,而sum[u]中已经记录过了串个数所以不用乘上,但c要乘上个数.最后答案就是所有节点sum的和
代码在这里
后缀自动机五·重复旋律8
题意
有N个询问,每个询问有字符串T,他们可以把第一个字符换到最后面成为T’,可以对T’进行相同的操作成为新的T’,在 给出的字符串S中,求对于每一个字符串T的所有T’在S中出现的次数和
S和T都小写字母组成, ∣ S ∣ , ∑ ∣ T ∣ ≤ 1 0 5 |S|, \sum|T|\le 10^5 ∣S∣,∑∣T∣≤105
思路
经典的计算字符串 T T T 每个位置的后缀在 S S S 中出现的最大长度问题,可以利用SAM的ch数组,因为通过ch数组所能跑出来串一定是 S S S 的子串,并且失配可以跳pre以保证最大长度匹配.方法:假设当前以及匹配到了u节点匹配长度为l,现在 T T T 中字符为c,判断 c h [ u ] [ c ] ch[u][c] ch[u][c] 是否有值,如果有 u = c h [ u ] [ c ] , l + + u=ch[u][c],l++ u=ch[u][c],l++ 否则 u = p r e [ u ] u=pre[u] u=pre[u] 以降低限制再重复上述操作,如果最后u=0则说明 T T T 根本在 S S S 中没有出现过,初始化u=1,l=0,否则u在保证 m x l [ u ] ≥ ∣ T ∣ mxl[u]\ge |T| mxl[u]≥∣T∣ 下继续跳pre[u],以保证相同的 T T T 都会到达相同的节点u,保证不会算重,最后对u打上标记, a n s + = s z [ u ] ans+=sz[u] ans+=sz[u] (sz[u]为endpos集合大小)
这种判断子串 T T T 在 S S S 中出现的次数的题可以改编成在 S S S 中的指定区间 [ l , r ] [l,r] [l,r] 中出现的次数,方法如上但要有线段树维护endpos节点判断是否在 [ l , r ] [l,r] [l,r] 区间中,"NOI2019你的名字"就是如此
代码在这里 倍增一下也可以
后缀自动机六·重复旋律9
题意
有A和B两个字符串,A’和B’分别是A和B的子串,小Hi和前辈分别可以选择A’和B’中的一个在其末尾添加一个字符,并要求添加后的串依然是A或B的一个子串,谁最后无法操作就输了.小Hi和前辈都足够聪明,小Hi和前辈一共进行K次较量,每次较量都是前辈先操作,前辈已经洞悉了所有先手必胜的A’和B’,第i次前辈会选出字典序第i小的A’和B’(A’优先级高于B’)和小Hi较量,请问第K次前辈会选出哪两个A’和B’?
K ≤ 1 0 18 ∣ A ∣ , ∣ B ∣ ≤ 1 0 5 K\le 10^{18}\quad |A|,|B|\le 10^5 K≤1018∣A∣,∣B∣≤105
思路
这道题时hihocoder后缀自动机最后一题,难度很高,其中用的SAM找第k小的思路可以先看看下面的[TJOI2015]弦论这道题,会更好的理解这里的方法
看到是博弈问题还和字符串有关,规则还是在字符串后加新的字符并且还是原串的子串,于是想到SAM的ch数组,通过SAM的ch数组走出来的串一定是其子串,原题的较量其实就变成SAM上的DAG(有向无环图)上进行的移动,可以想象成两个棋子在DAG上移动,谁先不能移动就输了.这是其实就是经典的DAG上组合游戏,利用SG函数判断是否有解,对于两个串只要判断对于节点的SG值异或值是否是0,如果是0则先手必败,否则先手必胜.
看到判断先手必胜可以通过SG函数,那么如何求出字典序第K小的A’和B’.我们先考虑在A上取一个节点,其对应的SG值记为 S G A SG_A SGA 考虑要求先手必胜则在B上取得一个节点的 S G B ≠ S G A SG_B \ne SG_A SGB̸=SGA 的所有节点都可以取到,我们记 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示拓扑序在i之后的所有SG值为j的节点个数和,记 s u m [ i ] = ∑ j ∈ C d p [ i ] [ j ] sum[i]=\sum_{j\in C} dp[i][j] sum[i]=∑j∈Cdp[i][j] C为字符集大小.于是我们可以通过 s u m [ i ] − d p [ i ] [ j ] sum[i]-dp[i][j] sum[i]−dp[i][j] 计算出所有i节点后的SG值不等于j的个数.问题可以得到解决,方法:记nowA为枚举到字符串A的SAM上的节点,nowB为枚举到字符串B的SAM上的节点,先枚举nowA的位置,通过判断剩余的K是否小于 B . s u m [ S G A ] − B . d p [ 1 ] [ S G A ] B.sum[SG_A]-B.dp[1][SG_A] B.sum[SGA]−B.dp[1][SGA] 如果是的则就是当前位置,否则 K − = B . s u m [ S G A ] − B . d p [ 1 ] [ S G A ] K-=B.sum[SG_A]-B.dp[1][SG_A] K−=B.sum[SGA]−B.dp[1][SGA] 再枚举c判断 c h [ n o w A ] [ c ] ch[nowA][c] ch[nowA][c] 是否可取,当 ∑ j ∈ C A . d p [ A . c h [ n o w A ] [ c ] ] [ j ] ∗ ( B . s u m [ 1 ] − B . d p [ 1 ] [ j ] ) ≥ K \sum_{j\in C} A.dp[A.ch[nowA][c]][j]*(B.sum[1]-B.dp[1][j]) \ge K ∑j∈CA.dp[A.ch[nowA][c]][j]∗(B.sum[1]−B.dp[1][j])≥K 则 n o w A = c h [ n o w A ] [ c ] nowA=ch[nowA][c] nowA=ch[nowA][c] 否则继续枚举c,如果枚举完了都没法转移 n o w A nowA nowA 则说明无解.然后继续枚举nowB的节点,方法和枚举A差不多,也是由字典序小到大判断是否可取,能取就取.
在每次移动nowA和nowB的时候记录下转移的c,最后答案就是nowA和nowB移动轨迹组成的串
这样讲解太麻烦,其实代码不难理解,看hihocoder其实也很好理解
代码在这里
单一的SAM
【模板】后缀自动机
题意
请你求出S的所有出现次数不为1的子串的出现次数乘上该子串长度的最大值。
∣ S ∣ ≤ 1 0 6 |S| \le 10^6 ∣S∣≤106
思路
先用基数排序算出每个节点的出现次数记为sz[i], a n s = M a x i ∈ [ 1 , c n t ] s z [ i ] ∗ m x l [ i ] ∗ [ s z [ i ] > 1 ] ans=Max_{i\in [1,cnt]}sz[i]*mxl[i]*[sz[i]>1] ans=Maxi∈[1,cnt]sz[i]∗mxl[i]∗[sz[i]>1]
式子中的中括号[一个条件]表示满足条件则为1否则为0.
代码在这里
工艺
题意
给你一个长度为n的有数字组成的序列,你可以将最左边的数字移动到最右边,你可以重复这个操作无限次,求出最小字典序的序列.
思路
看到可以把序列最前的移动到最后,于是把串重复插入到SAM中两次,在SAM上ch数组跑出来的都是它的子串,所以只要沿着字典序最小的ch跑一遍,直到长度到n结束.由于是数字组成的ch数组换成map即可.
代码在这里
[AHOI2013]差异
题意
给定一个长度为n的字符串S,令 T i T_i Ti 表示它从第i个字符开始的后缀.len(a)表示字符串a的长度,lcp(a,b)表示字符串a和字符串b的最长公共前缀,求
∑ 1 ≤ i < j ≤ n l e n ( T i ) + l e n ( T j ) − 2 ∗ l c p ( T i , T j ) \sum_{1\le i<j\le n} len(T_i)+len(T_j)-2*lcp(T_i,T_j) 1≤i<j≤n∑len(Ti)+len(Tj)−2∗lcp(Ti,Tj)
∣ S ∣ ≤ 5 ∗ 1 0 5 |S|\le 5*10^5 ∣S∣≤5∗105
思路
仔细看看式子,想想后缀树,在后缀树上找到A节点包含a串,B节点包含b串 l c a ( A , B ) lca(A,B) lca(A,B) 的节点一定包含 l c s ( a , b ) 最 长 公 共 后 缀 lcs(a,b)最长公共后缀 lcs(a,b)最长公共后缀 ,题目要求最长公共前缀就把SAM倒着建出来,答案其实就是要求树上任意两点间的距离和,令树上u到pre[u]的边权为 m x l [ u ] − m x l [ p r e [ u ] ] mxl[u]-mxl[pre[u]] mxl[u]−mxl[pre[u]] ,发现一共有 s z [ u ] ∗ ( n − s z [ u ] ) sz[u]*(n-sz[u]) sz[u]∗(n−sz[u]) 个点对经过这条边,sz[u]为u的子树大小,可以用基数排序计算,所以答案就是
a n s = ∑ i ∈ [ 1 , c n t ] ( m x l [ p r e [ i ] ] − m x l [ i ] ) ∗ s z [ u ] ∗ ( n − s z [ u ] ) ans = \sum_{i\in [1,cnt]}(mxl[pre[i]]-mxl[i])*sz[u]*(n-sz[u]) ans=i∈[1,cnt]∑(mxl[pre[i]]−mxl[i])∗sz[u]∗(n−sz[u])
cnt为SAM的节点总数
代码在这里
[TJOI2015]弦论
题意
给定一个串S求出它的第k小子串是什么?当t为0则表示不同位置的相同子串算作一个,t为1则表示不同位置的相同子串算作多个.若子串数目不足k个则输出-1.
∣ S ∣ ≤ 5 ∗ 1 0 5 k ≤ 1 0 9 |S|\le 5*10^5\quad k\le 10^9 ∣S∣≤5∗105k≤109
思路
又看到和字典序有关的子串题,想到上面的后缀自动机六·重复旋律9这道题其实思路一样,但这道题比上面的简单很多,只要预处理出它们后续节点数之和,当t=0时初始所有sz都为0,当t=1时通过基数排序算出每个节点的sz大小,再拓扑排序从大到小,依次计算出其 s u m [ u ] = ∑ s u m [ c h [ u ] [ c ] ] , c ∈ C sum[u]=\sum sum[ch[u][c]],c\in C sum[u]=∑sum[ch[u][c]],c∈C C为字符集大小,当 s u m [ 1 ] < k sum[1]<k sum[1]<k 输出-1,否则dfs从1开始每个节点从0-25枚举每种字符接在当前节点后面,当 s u m [ c h [ u ] [ c ] ] ≥ k sum[ch[u][c]]\ge k sum[ch[u][c]]≥k 时 u = c h [ u ] [ c ] u=ch[u][c] u=ch[u][c] 最后答案字符串就是u的移动轨迹组成的串.
代码在这里
LCS2 - Longest Common Substring II
题意
给定一些n个字符串,求出它们的最长公共子串长度.
n ≤ 10 ∑ ∣ S ∣ ≤ 1 0 6 n\le 10 \quad \sum |S| \le 10^6 n≤10∑∣S∣≤106
思路
由于是要求公共子串,所以可以仅对第一个字符串构造SAM,于是就变成了经典的计算字符串 T T T 每个位置的后缀在 S S S 中出现的最大长度问题,解决方法见上:后缀自动机五·重复旋律8.对每个节点记下当前最大的匹配长度,并用当前节点的最大匹配长度更新它所有的pre节点 m x [ u ] = m a x { m i n ( m x [ v ] , m x l [ u ] ) } , u ∈ P r e v mx[u]=max\{min(mx[v],mxl[u])\},u\in Pre_v mx[u]=max{min(mx[v],mxl[u])},u∈Prev, P r e v Pre_v Prev 是v的所有pre节点的集合,也可以理解成后缀树上它到根节点路径上的所有节点的集合.然后再对节点取最小值, m n [ u ] = m i n { m x [ u ] } mn[u]=min\{mx[u]\} mn[u]=min{mx[u]},意思就是在整体上这个节点的最大的匹配长度,对每个串重复上述操作,最终最大的mn[u]就是答案最长公共子串长度
LCS - Longest Common Substring是它的弱化版只有2个串
代码在这里
广义SAM
JZPGYZ - Sevenk Love Oimaster
题意
给定n个模板串S和m个查询串T,依次查询每一个查询串是多少个模板串的子串.
∣ S ∣ ≤ 1 0 5 ∣ T ∣ ≤ 3.6 ∗ 1 0 5 |S|\le 10^5 \quad |T| \le 3. 6*10^5 ∣S∣≤105∣T∣≤3.6∗105
思路
广义SAM的第一种构造方法(第二种构造方法在"[Zjoi2015]诸神眷顾的幻想乡"中会有),非常简单,只要在每次新加入一个串时把last=1即可.(注意:这样直接搞是不能做基数排序的,原因见广义后缀自动机上基排的一个bug - BlackJack,下面"[HAOI2016]找相同字符"一道题的广义SAM会用到特判操作以保证基数排序的正确性).
把所有的串都塞进广义SAM中,然后对每个串的所有子串在SAM节点上++sum,详细方法:枚举每个串的位置对应的SAM中节点x,x不断地跳pre,跳到的节点一定是它的子串,对节点++sum[x],为保证不加重复,还要对其打上标记.最后对每次询问,将询问串直接在广义SAM中ch数组上跑,如果断掉了说明在它不属于任何一个模板串的子串,直接结束.否则答案就是最后停下节点位置的sum值.
代码在这里
[USACO17DEC]Standing Out from the Herd
题意
定义一个字符串的"独特值"为只属于该字符串的本质不同的非空子串的个数.给定N个小写英文字母的字符串求出每个字符串的"独特值"
如"amy"和"tommy"两个串,只属于"amy"的本质不同的非空子串为"a",“am”,“amy"共3个,只属于"tommy"的本质不同的非空子串为"t”,“to”,“tom”,“tomm”,“tommy”,“o”,“om”,“omm”,“ommy”,“mm”,"mmy"共11个,所以它们的独特值分别为3和11
∣ S ∣ ≤ 1 0 5 |S|\le 10^5 ∣S∣≤105
思路
还是用到广义SAM构建方法如上道题一样,然后也是把每个串的所有子串++cnt,表示这个节点是多少串的公共子串,最后在分别对每个串找子串,其"独特值"就是它的子串中cnt=1的节点(即它只在一个串中出现过)的 m x l [ i ] − m x l [ p r e [ i ] ] mxl[i]-mxl[pre[i]] mxl[i]−mxl[pre[i]] 之和.代码中直接记录了经过当前节点的串的序号.
代码在这里
[HAOI2016]找相同字符
题意
给定两个字符串,求出在两个字符串中各取出一个子串使得两个子串相同的方案数.方案的不同有且仅当这两个串中有一个位置不同.
∣ S 1 ∣ , ∣ S 2 ∣ ≤ 2 ∗ 1 0 5 |S_1|,|S_2|\le 2*10^5 ∣S1∣,∣S2∣≤2∗105
思路
在上面两道题中都没有提到广义SAM构造要特判的细节,如果想用基数排序必须要特判一下.题目要求两个字符串的本质不同的公共子串的出现次数,想到要用到SAM上的sz[]即 ∣ e n d p o s ∣ |endpos| ∣endpos∣ 集合大小来判断,在普通SAM中求sz[]可以通过基数排序完成,在广义SAM上是否可行呢?当然可以,但要有一个前提,即节点的mxl顺序必须和拓扑排序顺序一致,说明我们不能构造出多余的节点.多余的节点只有可能出现在last=1时重新插入新串时,当 c h [ l a s t ] [ c ] ch[last][c] ch[last][c] 已经有值且 m x l [ c h [ l a s t ] [ c ] ] = = m x l [ l a s t ] + 1 mxl[ch[last][c]] == mxl[last] + 1 mxl[ch[last][c]]==mxl[last]+1 的时候,这个新的np节点就是无用的了.它不用插入SAM中,它是某个已经插入的串的一个子串,所以当 c h [ l a s t ] [ c ] ch[last][c] ch[last][c] 有值得时候,修改 l a s t = c h [ l a s t ] [ c ] last=ch[last][c] last=ch[last][c] 然后直接退出即可.
这道题要求两个串上相同串出现次数的组合,即要分别求 s z [ ] sz[] sz[],当一个节点在两个串上同时出现过,那么 s z [ i ] [ 1 ] 和 s z [ i ] [ 2 ] sz[i][1]和sz[i][2] sz[i][1]和sz[i][2] 都不为0, a n s + = s z [ i ] [ 1 ] ∗ s z [ i ] [ 2 ] ∗ ( m x l [ i ] − m x l [ p r e [ i ] ] ) ans+=sz[i][1]*sz[i][2]*(mxl[i]-mxl[pre[i]]) ans+=sz[i][1]∗sz[i][2]∗(mxl[i]−mxl[pre[i]]) 即可.
当然如果不想去除多余点,也可以直接dfs广义SAM,在回溯的时候也可以获得sz[]
基排代码 dfs代码
[ZJOI2015]诸神眷顾的幻想乡
题意
有一颗n个节点的树,每个节点一种颜色 c i c_i ci ,选中树上两点A和B(A,B可相同),A到B的路径上(包括端点)的颜色会组成一条序列(串),请问在这颗树上一共有多少不同的颜色序列(子串)?
树叶子节点不会超过20个. n ≤ 1 0 5 , c ∈ [ 1 , 10 ] n\le 10^5,c\in [1,10] n≤105,c∈[1,10]
思路
题目要求的就是多个串的本质不同的公共子串的个数,就要用到广义SAM.这道题就是构建广义SAM的第二种方法,先把所有的要插入的串都放到Trie树上,再从根节点遍历整颗Trie树,添加节点的时候从它的父节点在SAM中的节点后继续添加,这样就可以避免重复添加相同前缀的串.对于这道题而言,它相当于已经把字符串已经放在Trie树上了于是从每个叶子节点开始遍历整棵树,插入到SAM中,因为叶子节点一共只有20个复杂度为 O ( 20 ∗ n ) O(20*n) O(20∗n) 求有多少个本质不同的公共子串即 ∑ i ∈ [ 1 , c n t ] m x l [ i ] − m x l [ p r e [ i ] ] \sum_{i\in[1,cnt]}mxl[i]-mxl[pre[i]] ∑i∈[1,cnt]mxl[i]−mxl[pre[i]] 也就是后缀自动机二·重复旋律5的式子
代码在这里
ACM-ICPC WF2019 G题 First of her name
题意
第一行输入n和k,下面n行,每一行有一个英文大写字符c和一个数字i,表示该行的字符串是由第i行字符串的前端插入c字符所构成的新串(i=0表示它是独立的第一个字符,理解成插入在空串前面),题目保证不会出现相同的字符串,再下面k行,每行一个字符串S,询问S是多少个串的前缀?
样例:
10 5
S 0
Y 1
R 2
E 3
N 4
E 5
A 6
D 7
Y 7
R 9
RY
E
N
S
AY
解释:每一行字符串分别对应的是:
S
YS
RYS
ERYS
NERYS
ENERYS
AENERYS
DAENERYS
YAENERYS
RYAENERYS
询问中:"RY"是第3个和第10个串前缀,"E"是第4个和第6个串前缀,"N"是第5个串前缀,"S"是第1个串的前缀,"AY"不是任何一个串的前缀,输出0.
n ≤ 1 0 6 , ∑ ∣ S ∣ ≤ 1 0 6 n\le 10^6,\sum|S|\le 10^6 n≤106,∑∣S∣≤106
思路
看懂题意后,其实他给你了一颗Trie树,题中每一行的数字就是该节点的父亲节点,从Trie树根节点到树上任何一个节点走出的路径都是一个模板串,求询问串是多少个模板串的前缀.于是就和[ZJOI2015]诸神眷顾的幻想乡一样的思路,利用Trie树构建广义SAM,pos为Trie树上节点到根节点路径组成的串在SAM上对应的节点,每次插入新节点在Trie树上的父亲节点的pos后插入,在每个新插入位置的sz上+1,再求出每个节点的sz大小,询问就是把询问串倒过来走ch数组,如果中间走不下去了就说明它不是任何一个串的子串输出0,否则输出最后它到达的节点的sz值.
问题来了,为什么我用基排和用dfs求sz数组,为什么dfsA了而基排WA了呢,理论上在Trie树上构建SAM是没有多余节点问题的,而且题目保证了没有相同的串,为什么基排挂了呢?求大佬解释.
AC代码dfs版 WA代码基排版
SAM+DP
[CTSC2012]熟悉的文章
题意
给定M个模板串,如果一个01串S将其分割成若干段子串,其中是模板串的子串的串的长度和不少于S总长度的90%那么称S是"熟悉的文章",求让S成为"熟悉的文章"的所有子串的长度的最大值.一共有N次询问
输入文件的总长度不超过 1.1 ∗ 1 0 6 1.1*10^6 1.1∗106 字节
思路
发现当答案越小与模板串匹配数肯定越多,答案越大与模板串匹配数越少,于是可以二分答案.
那么如何去写check函数呢?这里必须要做到接近 O ( n ) O(n) O(n) 的速度.我们先预处理出每个节点的最大后缀匹配长度记为mxc[i],求这个方法可以把要求的串再广义SAM上ch数组上找到其匹配最大长度.
于是问题变成了如何去把串分段,使得匹配长度最大.这里肯定要用到dp,记f[i]表示匹配到i时前面(包含i)的匹配最大长度,记我们check的长度为L,我们每次分段的长度为 [ m x c [ i ] , L ] [mxc[i],L] [mxc[i],L] ,于是有转移方程 f [ i ] = m a x { f [ i − 1 ] , f [ j ] + i − ( j + 1 ) + 1 } , j ∈ [ i − m x c [ i ] , i − L ] f[i]=max\{f[i-1],f[j]+i-(j+1)+1\},j\in [i-mxc[i],i-L] f[i]=max{f[i−1],f[j]+i−(j+1)+1},j∈[i−mxc[i],i−L] 对于每个位置,我们只要 f [ j ] + i − j f[j]+i-j f[j]+i−j 的最大值,发现 i − m x c [ i ] i-mxc[i] i−mxc[i] 是单调不降序列,于是可以用单调队列维护最大值,要求最大值 f [ j ] − j f[j]-j f[j]−j 于是可以维护一个 f [ j ] − j f[j]-j f[j]−j 单调递减队列,每次队头就是最优转移方案,细节请看代码.
代码在这里
SAM+LCT
「雅礼集训 2017 Day7」事情的相似度
题意
给出一个01串,求出结束点在 [ l , r ] [l,r] [l,r] 的两个前缀的最长公共后缀长度
思路
i , j i, j i,j 表示原字符串上位置, p o s [ ] pos[] pos[] 表示在SAM上对应的点
求两个点的最长公共后缀长度,就是他们在后缀树上的LCA点的 m x l mxl mxl
先把询问离线下来,按右端点排序,从左向右顺着扫一遍,每次把当前点 p o s [ i ] pos[i] pos[i] 到根节点的路径都打上 i i i 位置标记,如果新加入的点到根的路径上找到了标记,那么就要更新这个点的 m x l mxl mxl 对答案的贡献
p o s [ i ] pos[i] pos[i] 到根节点的路径就是LCT的access操作,顺便找出打过标记的点
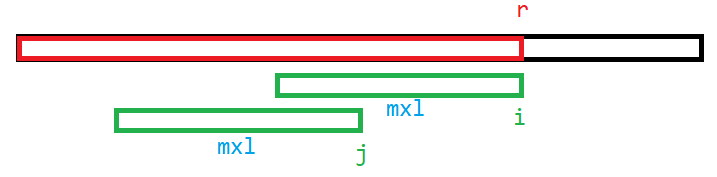
如图,当前右端点已经到了 r r r 在进行access操作时,找到了 j j j 节点,那么在线段树上 j j j 的mx值就可以更新成 m x l mxl mxl ,在线段树上查询区间 [ l , r ] [l,r] [l,r] 时,当 l l l 在 j j j 的右边时,这个 m x l mxl mxl 不会对答案贡献,当 l l l 在 j j j 的左边时,这个 m x l mxl mxl 可能对答案贡献。所以只需要在线段树上更新 j j j 的mx值
当结束完一个点的access操作和query后,再对它打上标记
题解和代码