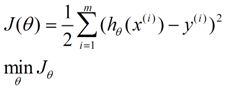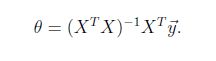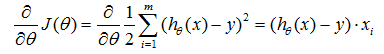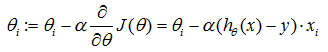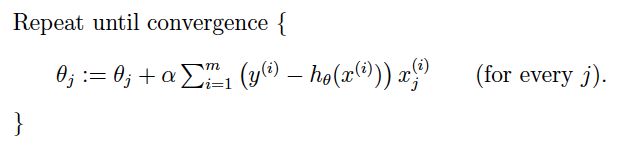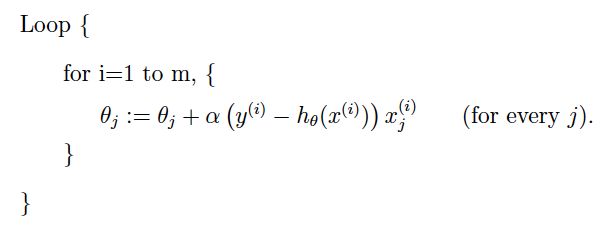线性回归模型及梯度下降算法(吴恩达机器学习第一周作业)
1. 线性回归
引例:房屋估价系统
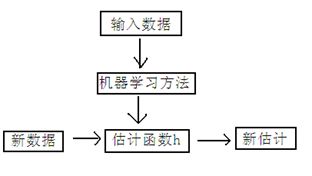
房屋估价系统问题就是当知道房屋面积、卧室个数与房屋价格的对应关系之后,在得知一个新的房屋信息后如何得到对应的新房屋价格,这类问题可以简化为:
寻找房屋面积、卧室个数与房屋价格之间关系方程的过程就是回归,这里假设他们之间是线性关系,即房屋价格可以被表示为房屋面积与卧室个数的一维线性方程,如:
![]()
这里x表示与房屋价格相关的特征,x1为房屋面积,x2为卧室个数,θ可以理解为各个特征的影响权重。
抽象地总结一下
回归:用一条曲线对数据点进行拟合,该曲线称为最佳拟合曲线,这个拟合过程叫做回归。回归问题的求解过程就是通过训练分类器采用最优化算法来寻找最佳拟合参数集。
线性回归:当该曲线为一条直线时,就是线性回归。其中,“线性”是指特征和结果都是线性的,即不大于一次方,每个分量表示一个特征,向量表示为:
![]()
h=hypothesis,是特征函数的估计表达式,由于求解一个含有参数众多的线性矩阵方程,需要建立足够的约束条件才能得到唯一解。
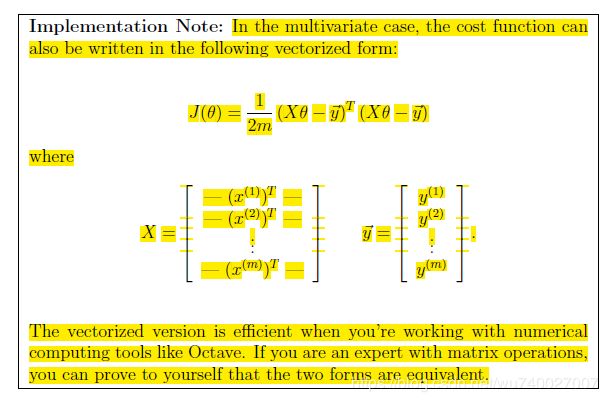
实际上由于条件有限,大多数情况下都是求解超定方程组的近似最优解,即满足使得估计值与实际值的方差最小时的参数解,可以表示为:
这就是损失函数,求解的方法有最小二乘法、梯度下降法等。
线性损失函数的求解方法:
- 最小二乘法,求误差的最小平方和,非线性最小二乘法无闭式解,一般通过迭代法求解;而线性最小二乘有闭式解,通过一系列的数学推导,可以得到一个标准方程:
- 梯度下降法,利用沿着梯度下降最快的方向求偏导数,得到损失函数的全局最小值时的参数θ,涉及到偏导数、学习速度、更新、收敛等问题。
非线性最小二乘法的求解方法:
- 高斯牛顿法,常用于求解非线性最小二乘的迭代法,可视为标准非线性最小二乘求解方法。
- Levenberg-Marquardt迭代法,求解非线性最小二乘问题,结合了梯度下降和高斯-牛顿法。
2. 梯度下降法
- 梯度下降法的思想:
1)首先对θ赋值,这个值可以是随机的,也可以是一个零向量;
2)改变θ的值,使得J(θ)按梯度下降的方向进行减少;
3)当J(θ)下降到无法下降时为止,即J(θ)对θ的导数为0时,比较J(θ)的值是否有变化。
对损失函数J(θ)求偏导,得到:
- 参数更新过程:
更新过程可以理解成:θi沿着梯度下降最快的方向进行递减的过程。
左边的θi表示更新之前的值,等式右边表示沿着梯度方向减少的量,α表示步长,也称作学习速度,这个值需要人工手动设置。
不断更新θi的值直到J(θ)收敛,可以通过比较J(θ)的前后两个值是否有发生变化(继续下降),当没有发生变化时表示已经达到了最小值(可能是局部最小值)。
- 参数设置问题:
初始值和学习速度都是是人工设置的,而梯度下降法对这些参数又是敏感的。
初始值的设置会影响到最终J(θ)的最小值,它可能是局部最小值,也可能是全局最小值。
学习速度的设置也会影响到梯度下降的性能和结果:
1)当设置过小时,由于沿着最陡峭方向每次迈进的步伐太小,而导致收敛时间过长;
2)当设置过大时,很有可能会直接越过最小值,而无法得到J(θ)的最小值。
- 梯度下降法的改进:
上述梯度下降法也叫批量梯度下降法(Batch gradient descent),每次迭代都需要用到训练集所有的数据,收敛速度较慢。
因此,得到它的改进算法随机梯度下降法(Stochastic gradient descent),也叫增量梯度下降法(Incremental gradient descent)。
随机梯度下降通过每个样本来迭代更新一次参数,可能未遍历整个样本就已经找到最优解,大大提高了算法的收敛速度。
最小化每个样本的损失函数,虽然每次迭代结果不一定都是全局最优解,却总是沿着这个方向发展,故最终结果总是接近全局最优解。
下面是具体实现的过程:
1.先将数据加载到OCTAVE中,并且把ex1data1中的内容读取到X变量和y变量中,用m表示数据长度。
| 1 2 3 4 |
|
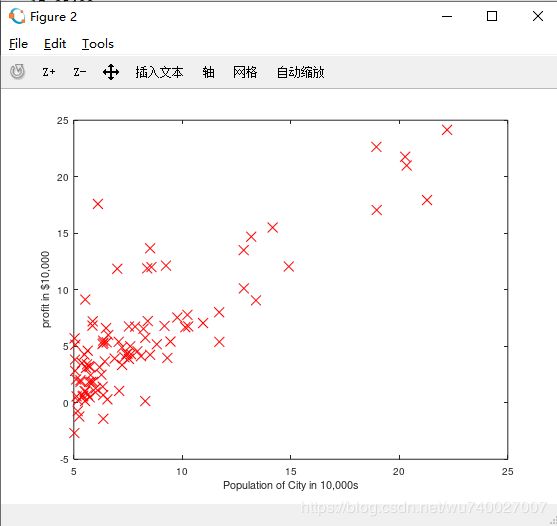
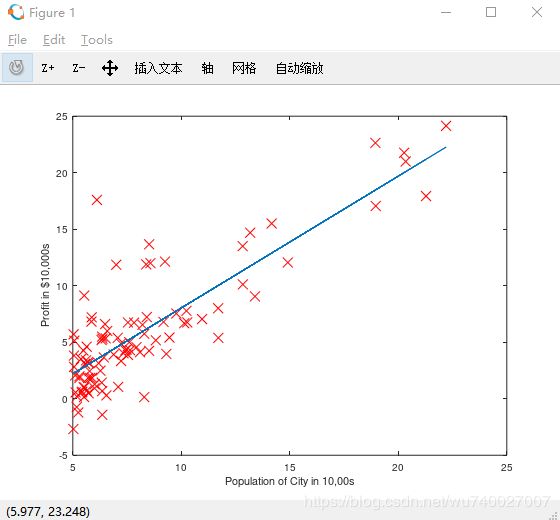
之后将数据点在用图像画出来
| 1 2 3 |
|
绘图函数:
然后是梯度下降函数:
之后就可以进行梯度下降了:
之后根据theta来画出对应的函数
至此,我们通过梯度下降法解决了此问题,我们还可以通过之前所说的数学方法来解决,但是对于数据太大的情况(通常大于10000),我们就会通过梯度下降法来解决了。
数学方法: