杭电1166——线段树（单点更新）

杭电acm1166——线段树（单点更新）

---

线段树只是acm众多算法中的很普遍的一种，但是他的效率非常高，一般算法复杂度为o（n）的题，通过线段树之后，就会变成o（log2（n）），本文是以杭电acm1166题举例，来对线段树进行一些了解：杭电1166原题链接

题解：
查询某个区间的总人数，因为阵营个数和每个阵营的人数上限都比较大，所以如果暴力解决的话，肯定会超时，这个时候就需要线段树，首先用一张图片来简单的解释一下线段树：

比如说求5到12的总人数，用线段树的话，你只要找到【5,7】、【8，10】、【11,12】这三个部分，加起来就是所求的值。比5+6+7+···+11+12效率多了。
线段树有三个函数，建树、更新、查询。

---

在开始之前需要定义一个结构体，用来存储线段树节点的各种值

struct st{
	int l;//区域的左界
	int r;//区域的右界
	int n;//区域内的和
}s[50000 * 4];//这里需要上限×4，防止溢出，

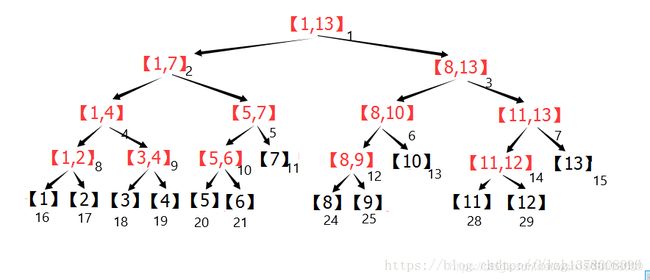
建树的时候，需要用一个数组来存储数据，用来以后访问各个节点的数据。
访问线段树的方法：例如当前访问的节点是【1,4】这个节点，用s[4]表示，那么访问左孩子节点的时候可以用s[2×4]，即s[8]；访问右孩子节点的时候可以用s[2×4+1]，即s[9]。

//建树
/*
传入的参数：
l：左界限
r：右界限
k：刚开始的下标值
*/
void bulid(int l, int r, int k) {
	s[k].l = l;
	s[k].r = r;
	s[k].n = 0;//赋值
	if (l == r) {//如果左界=右界，说明枝杈已经创建成功，不能继续往下创建了
		return;
	}
	int mid = (l + r) / 2;
	bulid(l, mid, 2 * k);//创建k的左枝
	bulid(mid + 1, r, 2 * k + 1);//创建k的右枝
}

更新

/*
传入的参数：
d：需要修改的值
n：增加的值（如果是减少，传参的时候传入负值就可以）
k：刚开始的下标值
*/
void insert(int d, int n, int k) {
	if (s[k].l == s[k].r && s[k].l == d) {
		s[k].n += n;//如果k的左界和右界都和d相等，说明k节点就是需要修改的数值，s[k].n加上n，然后返回。
		return;
	}
	int mid = (s[k].l + s[k].r) / 2;//取中间点
	if (d <= mid) {//如果d<=中间值，就去寻找k的左枝
		insert(d, n, 2 * k);
	}
	else {//如果d>中间值，就去寻找k的右枝
		insert(d, n, 2 * k + 1);
	}
	s[k].n = s[2 * k].n + s[2 * k + 1].n;//每次使用更新函数的时候都需要更新每个节点上n的值
}

查找

int ans;//这里需要一个全局变量，用来存储答案。
/*
传入的参数：
l：查找的左界
r：查找的右界
k：刚开始的下标值
*/
void fin(int l, int r, int k) {
	if (s[k].l == l && s[k].r == r) {
		ans += s[k].n;
	//如果需要查找的左（右）界和k节点的左（右）界相等，说明k节点代表的区域是答案的一部分，ans需要加上k节点的n。
		return;
	}
	int mid;
	mid = (s[k].l + s[k].r) / 2;
	if (r <= mid) {
		fin(l, r, 2 * k);//如果r<=mid，说明答案只存在k的左枝。
	}
	else if (l>mid){
		fin(l, r, 2 * k + 1);//如果l>mid，说明答案只存在k的右枝。
	}
	else {//否则左右枝都需要查找
		fin(l, mid, 2 * k);
		fin(mid+1, r, 2 * k+1);
	}
}

整理一下：

# include 
# include 
# include 
# include 
using namespace std;

struct st{
	int l, r, n;
}s[50000*4];

/*
传入的参数：
l：左界限
r：右界限
k：刚开始的下标值
*/
void bulid(int l, int r, int k) {
	s[k].l = l;
	s[k].r = r;
	s[k].n = 0;//赋值
	if (l == r) {//如果左界=右界，说明枝杈已经创建成功，不能继续往下创建了
		return;
	}
	int mid = (l + r) / 2;
	bulid(l, mid, 2 * k);//创建k的左枝
	bulid(mid + 1, r, 2 * k + 1);//创建k的右枝
}

/*
传入的参数：
d：需要修改的值
n：增加的值（如果是减少，传参的时候传入负值就可以）
k：刚开始的下标值
*/
void insert(int d, int n, int k) {
	if (s[k].l == s[k].r && s[k].l == d) {
		s[k].n += n;//如果k的左界和右界都和d相等，说明k节点就是需要修改的数值，s[k].n加上n，然后返回。
		return;
	}
	int mid = (s[k].l + s[k].r) / 2;//取中间点
	if (d <= mid) {//如果d<=中间值，就去寻找k的左枝
		insert(d, n, 2 * k);
	}
	else {//如果d>中间值，就去寻找k的右枝
		insert(d, n, 2 * k + 1);
	}
	s[k].n = s[2 * k].n + s[2 * k + 1].n;//每次使用更新函数的时候都需要更新每个节点上n的值
}


int ans;//这里需要一个全局变量，用来存储答案。
/*
传入的参数：
l：查找的左界
r：查找的右界
k：刚开始的下标值
*/
void fin(int l, int r, int k) {
	if (s[k].l == l && s[k].r == r) {
		ans += s[k].n;
	//如果需要查找的左（右）界和k节点的左（右）界相等，说明k节点代表的区域是答案的一部分，ans需要加上k节点的n。
		return;
	}
	int mid;
	mid = (s[k].l + s[k].r) / 2;
	if (r <= mid) {
		fin(l, r, 2 * k);//如果r<=mid，说明答案只存在k的左枝。
	}
	else if (l>mid){
		fin(l, r, 2 * k + 1);//如果l>mid，说明答案只存在k的右枝。
	}
	else {//否则左右枝都需要查找
		fin(l, mid, 2 * k);
		fin(mid+1, r, 2 * k+1);
	}
}

int main() {
	int T,n,x;
	string str;
	int a, b;
	scanf("%d", &T);
	for (int i = 1; i <= T; i++) {
		printf("Case %d:\n", i);
		scanf("%d", &n);
		bulid(1,n,1);
		for (int j = 0; j < n; j++) {
			scanf("%d", &x);
			insert(j + 1, x, 1);
		}
		while (1) {
			cin >> str;
			if (str[0] == 'E') {
				break;
			}
			scanf("%d%d", &a, &b);
			if (str[0] == 'A') {
				insert(a, b, 1);
			}
			else if (str[0] == 'S') {
				insert(a, -b, 1);
			}
			else if (str[0] == 'Q') {
				ans = 0;
				fin(a, b, 1);
				printf("%d\n", ans);
			}
		}
	}
	return 0;
}

写在最后：输入输出的时候，一定要用scanf和printf，如果用cin和cout的时候，会超时的，我就是在这里卡了很久：用cin的时候超时了（超过1000ms），用scanf只有300ms左右。以前根本没想过cin会比scanf慢那么多（输入string字符串的时候用的是cin，因为string会方便很多，也可以用char的字符数组）。