算法系列(一)、归并排序
算法系列(一)、归并排序
概念的东西稍后上,我们先通过举例了解一下归并排序的工作过程
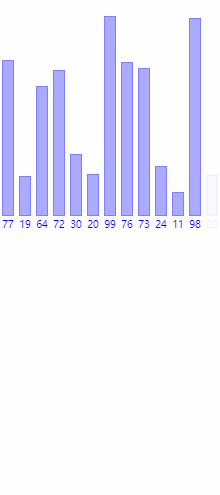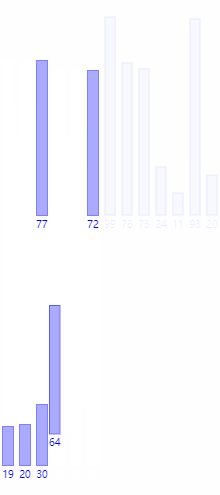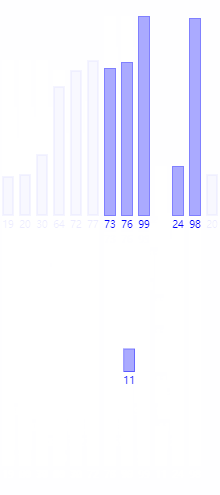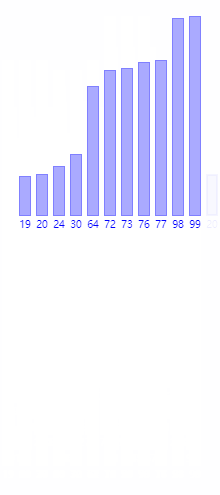
假设我们现在有[77,19,64,72,30,20,99,76,73,24,11,98]12个数,归并排序算法先将其分为分为前6个数和后6个数两组,并进行递归,对前6个数也从中间分为两组,直到每组数据只剩下两个数(若为单数的情况,则第一组数据为2个,第二组数据为1个数),此时比较这两个数的大小,并利用一个缓存数组进行交换排序:
那么第一步(或者叫第二层,第一层为原始数据)处理的数组是[77,19,64,72,30,20]和[99,76,73,24,11,98]
第二步(第三层)处理的数组是[77,19,64]和[72,30,20]
第三步(第四层):[77,19]和[64],比较第一个数组中两个数的大小,77>19,因此利用一个缓存数组在原始数组中交换这两个数的位置即,原始数组变为[19,77,64,72,30,20,99,76,73,24,11,98]
第四步(第四层):比较[19,77]和[64]中最小的两个数,把较小的一方存放到缓存数组的起始位,并向后移动指针,继续比较下一位,直到这3个数全部被放到缓存数组中(即指针指向数组的末位)当[72,30,20]也按照此方法比较完成后,回退到第三层,假设此时已经比较完成则得到两个虚拟数组[19,64,77]和[20,30,72],再按照这一步的方法,比较这两个虚拟数组的最小数(第一位),将较小的一方存放到缓存数组的起始位,向后移动指针,继续比较,直到生成的缓存数组如下:[19,20,30,64,72,77],这时根据指针位置,将缓存数组中的数据替换到待排序数组中即完成排序。
如下图:
当个数较多时:
最后,再回过头来看归并排序的概念和特性,是不是更容易理解了呢:
归并排序采用分治的思想:
- Divide:将n个元素平均划分为各含n/2个元素的子序列;
- Conquer:递归的解决俩个规模为n/2的子问题;
- Combine:合并俩个已排序的子序列。
性能:时间复杂度总是为O(NlogN),空间复杂度也总为为O(N),算法与初始序列无关,排序是稳定的。