抢红包算法--四种抢红包算法对比

        线上测试服务器中，有个同事做的抢红包算法被要求优化，大概听了下他们的讨论，最后的结果竟然要用什么概率论等等一系列我听过的、没听过的名词去解决。我表示一脸懵*。其实解决的问题就是一个：抢红包算法不够平均，先抢后抢有概率造成金额差值过大。

        针对这个问题的解决方法，有四种（普通法，线段切割法，双倍随机法，投篮球法）。前三种算法，网上基本都在流传，投篮球算法，是我自己瞎起的名字。这个算法还是因为当年校招，面试北京涂鸦移动，面试官现场引导我一个问题，用了投篮球这个例子。而我写这篇博客的时候，想起那个算法，蛮适用的，因而叫他投篮球算法。

        一、普通法：每次针对剩余总金额做一次随机，随机值就是第一个人的数值。这个算法也就是这个同事之前写的要求被优化的算法。这个算法的好处是完全随机，坏处是极有可能造成前人抢的太多，后人太少。例如，100元分给10个人，第一个人在0-100随机，均值为50。而第二个人的均值只剩25，之后是12.5。

//普通法    有保底
//iTotalGold总金额    iNum份数    iBaseGold保底金额
void oldThink(int iTotalGold, int iNum, int iBaseGold)
{
	if (iBaseGold*iNum > iTotalGold)
	{
		cout << "保底太多 " << iBaseGold< veGold(iNum);
	for (int i = 0; i < iNum-1; ++i)
	{
		int iAddNum = 0;
		if(iTotalGold != 0)
			iAddNum += rand() % (iTotalGold);
		veGold[i] = iAddNum + iBaseGold;
		iTotalGold -= iAddNum;
	}
	veGold[iNum - 1] = iTotalGold + iBaseGold;
	cout << "普通法:" << endl;
	copy(veGold.begin(), veGold.end(), ostream_iterator(cout, " "));
	cout << endl;
} 

        二、线段切割法：将总金额想象成一条那么长的线段，需要分割成num份，随机num-1次，将每次的随机值映射到该线段上。这样的好处是将随机交给程序，缺点是有小概率造成某个人分配过多。例如，100个人分10个红包，我们除了需要考虑随机值重合之外，每次完全随机，可能造成不够随机的情况。

//线段切割法    无保底
//iTotalGold总金额    iNum份数    iBaseGold保底金额
void cutline(int iTotalGold, int iNum)
{
	if (iNum > iTotalGold)
	{
		return;
	}
	if (iNum == iTotalGold)
	{
		for (int i = 0; i < iNum; ++i)
			cout << 1 << " ";
		cout << endl;
		return;
	}
	std::set setGold;
	for (int i = 0; i < iNum-1; ++i)
	{
		while (1)
		{
			int iPos = rand() % iTotalGold;
			if (setGold.find(iPos) == setGold.end())
			{
				setGold.insert(iPos);
				break;
			}
		}
	}
	cout << "线段切割法(无保底):" << endl;
	int iPreLine = 0;
	for (auto &it : setGold)
	{
		cout << it - iPreLine << " ";
		iPreLine = it;
	}
	cout << iTotalGold - iPreLine << " ";
	cout << endl;
}

         三、双倍随机法：每次随机的时候，取0-每个人平均金额的2倍进行随机。这样已经基本完成了我们想要的样子，不错的方法。例如：100个人分10分，每次随机都是0-100/10*2去随机，基本可以保证每个人平均在10左右，是相当平均的算法。不过需要注意最后几个人可能已经不足20的情况。

//双倍随机法
//iTotalGold总金额    iNum份数    iBaseGold保底金额
void twobase(int iTotalGold, int iNum, int iBaseGold)
{
	if (iNum *iBaseGold > iTotalGold)
	{
		cout << "保底太多 " << iBaseGold << endl;
		return;
	}
	std::vector veGold(iNum, iBaseGold);
	iTotalGold -= iNum*iBaseGold;
	int iBaseTmp = iTotalGold / iNum * 2;
	for (int i = 0; i < iNum - 1; ++i)
	{
		if (iTotalGold == 0)
			break;
		int iTmp = 0;
		if (iTotalGold >= iBaseTmp)
			iTmp = rand() % iBaseTmp;
		else
			iTmp = rand() % iTotalGold;
		veGold[i] += iTmp;
		iTotalGold -= iTmp;
	}
	veGold[iNum - 1] = iTotalGold;
	cout << "双倍随机法:" << endl;
	copy(veGold.begin(), veGold.end(), ostream_iterator(cout, " "));
	cout << endl;
}

       四、投篮球法：之前总是用金额去除以人数num以寻求平均。而投篮球法，则是以金额的单元值最为基准。以上三种算法都在极力的寻求随机，而投篮球法则是为了保证完全平均。例如：100个人分10分，每次取金额的最小单元值，比如一块钱，然后把10个人当成篮筐，一块钱当成篮球，每次都去投篮。这样的好处是不用模仿完全随机，他本身就是完全随机，坏处也很明显，循环次数过多。所以这里采用最小金额的单元值，例如每次取三块、五块。代码很简单：

//投篮球法    有保底
//iTotalGold总金额    iNum份数    iBaseGold保底金额
void basketball(int iTotalGold, int iNum, int iBaseGold)
{
	if (iBaseGold*iNum > iTotalGold)
	{
		cout << "保底太多 " << iBaseGold << endl;
		return;
	}
	iTotalGold -= (iBaseGold *iNum);
	std::vector veGold(iNum, iBaseGold);
	for (int i = 0; i < iTotalGold; i += 2) //这里基准值用了2，减少循环次数
	{
		int iPos = rand() % iNum;
		veGold[iPos] += 2;
	}
	cout << "投篮球法:" << endl;
	copy(veGold.begin(), veGold.end(), ostream_iterator(cout, " "));
	cout << endl;
}

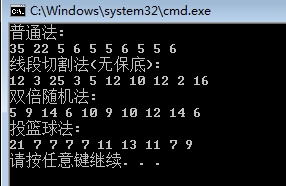
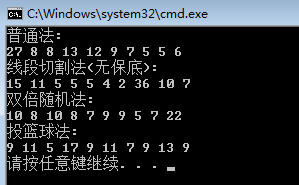
测试结果：

        测试了几次，目前最差的就是普通法，因为所有大金额全部集中在前几个人。双倍随机法和投篮球法基本上都在平均值附近，差值并非很大，但考虑到调用次数的话，双倍随机法生出，如果考虑到代码简洁的话，投篮球法稍好。线段切割法不适用于我们游戏中策划的需求，但是差值大一些的抢红包应该更适用于平时一些简单APP的应用。