SMO(Sequential minimal optimization)算法的详细实现过程
SMO算法主要是为优化SVM(支持向量机)的求解而产生的,SVM的公式基本上都可以推到如下这步:
m a x α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j max_{\alpha}\sum_{i=1}^{m}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j} maxα∑i=1mαi−21∑i=1m∑j=1mαiαjyiyjxiTxj
s . t . ∑ i m α i y i = 0 s.t. \sum_{i}^{m}\alpha_{i}y_{i}=0 s.t.∑imαiyi=0
0 ≤ α i ≤ C , i = 1 , 2 , 3 , . . . , m 0≤\alpha_{i}≤C,i = 1, 2, 3,...,m 0≤αi≤C,i=1,2,3,...,m
其中,C是SVM中惩罚参数(或正则化常数),可令:
φ ( α ) = ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j \varphi(\alpha)=\sum_{i=1}^{m}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j} φ(α)=∑i=1mαi−21∑i=1m∑j=1mαiαjyiyjxiTxj
SMO的具体步骤:
第一步:为了满足 ∑ i m α i y i = 0 \sum_{i}^{m}\alpha_{i}y_{i}=0 ∑imαiyi=0公式,首先要固定两个变量 α i 和 α j \alpha_{i}和\alpha_{j} αi和αj,这里以 α 1 和 α 2 \alpha_{1}和\alpha_{2} α1和α2为例,其余的 α i ( i = 3 , 4 , . . . , m ) 都 是 已 知 量 \alpha_{i}(i=3,4,...,m)都是已知量 αi(i=3,4,...,m)都是已知量,则约束条件变成:
α 1 y 1 + α 2 y 2 = c = − ∑ i = 3 m α i y i , ( 0 ≤ α 1 ≤ C , 0 ≤ α 2 ≤ C ) \alpha_{1}y_{1}+\alpha_{2}y_{2}=c=-\sum_{i=3}^{m}\alpha_{i}y_{i},(0≤\alpha_{1}≤C,0≤\alpha_{2}≤C) α1y1+α2y2=c=−∑i=3mαiyi,(0≤α1≤C,0≤α2≤C)
两边同乘 y 1 y_{1} y1,并记 y 1 y 2 = h 0 y_{1}y_{2}=h_{0} y1y2=h0得:
α 1 + h 0 α 2 = − y 1 ∑ i = 3 m α i y i = α 1 n e w + h 0 α 2 n e w \alpha_{1}+h_{0}\alpha_{2}=-y_{1}\sum_{i=3}^{m}\alpha_{i}y_{i}=\alpha_{1_{new}}+h_{0}\alpha_{2_{new}} α1+h0α2=−y1∑i=3mαiyi=α1new+h0α2new
令 H = − y 1 ∑ i = 3 m α i y i H=-y_{1}\sum_{i=3}^{m}\alpha_{i}y_{i} H=−y1∑i=3mαiyi,可得:
α 1 n e w = H − h 0 α 2 n e w \alpha_{1_{new}}=H-h_{0}\alpha_{2_{new}} α1new=H−h0α2new (1)
第二步:由于 α 1 n e w \alpha_{1_{new}} α1new可以用 α 2 n e w \alpha_{2_{new}} α2new来表示,且 α i ( i = 3 , 4 , . . . , m ) \alpha_{i}(i=3,4,...,m) αi(i=3,4,...,m)都是已知量,此时 φ ( α ) \varphi(\alpha) φ(α)只有一个未知变量 α 2 n e w \alpha_{2_{new}} α2new,那么可以直接求导得到 α 2 n e w \alpha_{2_{new}} α2new。具体实施过程如下:
1、展开 φ ( α ) \varphi(\alpha) φ(α)可得:
φ ( α ) = α 1 n e w + α 2 n e w − 1 2 α 1 n e w 2 k 11 − 1 2 α 2 n e w 2 k 22 − α 1 n e w α 2 n e w y 1 y 2 k 12 − α 1 n e w y 1 ∑ i = 3 m α i y i k i 1 − α 2 n e w y 2 ∑ i = 3 m α i y i k i 2 + φ c o n s t a n t \varphi(\alpha)=\alpha_{1_{new}}+\alpha_{2_{new}}-\frac{1}{2}\alpha_{1_{new}}^{2}k_{11}-\frac{1}{2}\alpha_{2_{new}}^{2}k_{22}-\alpha_{1_{new}}\alpha_{2_{new}}y_{1}y_{2}k_{12}-\alpha_{1_{new}}y_{1}\sum_{i=3}^{m}\alpha_{i}y_{i}k_{i1}-\alpha_{2_{new}}y_{2}\sum_{i=3}^{m}\alpha_{i}y_{i}k_{i2}+\varphi_{constant} φ(α)=α1new+α2new−21α1new2k11−21α2new2k22−α1newα2newy1y2k12−α1newy1∑i=3mαiyiki1−α2newy2∑i=3mαiyiki2+φconstant (2)
式中, k i j = k ( x i , x j ) kij=k(x_{i},x_{j}) kij=k(xi,xj),表示核函数
φ c o n s t a n t = ∑ i = 3 m α i − 1 2 ∑ i = 3 m ∑ j = 3 m α i α j y i y j k i j \varphi_{constant}=\sum_{i=3}^{m}\alpha_{i}-\frac{1}{2}\sum_{i=3}^{m}\sum_{j=3}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}k_{ij} φconstant=∑i=3mαi−21∑i=3m∑j=3mαiαjyiyjkij
2、SVM的超平面模型: f ( x j ) = w T + b = ∑ i = 1 m α i y i k i j + b f(x_{j})=w^{T}+b=\sum_{i=1}^{m}\alpha_{i}y_{i}k_{ij}+b f(xj)=wT+b=∑i=1mαiyikij+b
令 V j = ∑ i = 3 m α i y i k i j = f ( x j ) − b − α 1 y 1 k 1 j − α 2 y 2 k 2 j V_{j}=\sum_{i=3}^{m}\alpha_{i}y_{i}k_{ij}=f(x_{j})-b-\alpha_{1}y_{1}k_{1j}-\alpha_{2}y_{2}k_{2j} Vj=∑i=3mαiyikij=f(xj)−b−α1y1k1j−α2y2k2j (3)
3、 将公式(1)、(3)代入(2)得:
φ ( α ) = H − h 0 α 2 n e w + α 2 n e w − 1 2 ( H − h 0 α 2 n e w ) 2 k 11 − 1 2 α 2 n e w 2 k 22 − ( H − h 0 α 2 n e w ) α 2 n e w y 1 y 2 k 12 − ( H − h 0 α 2 n e w ) y 1 V 1 − α 2 n e w y 2 V 2 + φ c o n s t a n t \varphi(\alpha)=H-h_{0}\alpha_{2_{new}}+\alpha_{2_{new}}-\frac{1}{2}(H-h_{0}\alpha_{2_{new}})^{2}k_{11}-\frac{1}{2}\alpha_{2_{new}}^{2}k_{22}-(H-h_{0}\alpha_{2_{new}})\alpha_{2_{new}}y_{1}y_{2}k_{12}-(H-h_{0}\alpha_{2_{new}})y_{1}V_{1}-\alpha_{2_{new}}y_{2}V_{2}+\varphi_{constant} φ(α)=H−h0α2new+α2new−21(H−h0α2new)2k11−21α2new2k22−(H−h0α2new)α2newy1y2k12−(H−h0α2new)y1V1−α2newy2V2+φconstant
对 α 2 n e w \alpha_{2_{new}} α2new求导数可得:
d φ ( α ) d α 2 n e w = − ( k 11 + k 22 − 2 k 12 ) α 2 n e w + h 0 H ( k 11 − k 22 ) + y 2 ( V 1 − V 2 ) − h 0 + 1 = 0 \frac{d\varphi(\alpha)}{d\alpha_{2_{new}}}=-(k_{11}+k_{22}-2k_{12})\alpha_{2_{new}}+h_{0}H(k_{11}-k_{22})+y_{2}(V_{1}-V_{2})-h_{0}+1=0 dα2newdφ(α)=−(k11+k22−2k12)α2new+h0H(k11−k22)+y2(V1−V2)−h0+1=0
求解可得:
( k 11 + k 22 − 2 k 12 ) α 2 n e w = h 0 H ( k 11 − k 22 ) + y 2 ( V 1 − V 2 ) − h 0 + 1 (k_{11}+k_{22}-2k_{12})\alpha_{2_{new}}=h_{0}H(k_{11}-k_{22})+y_{2}(V_{1}-V_{2})-h_{0}+1 (k11+k22−2k12)α2new=h0H(k11−k22)+y2(V1−V2)−h0+1 (4)
此时,将 H 、 V j H、V_{j} H、Vj代入公式(4)可得:
( k 11 + k 22 − 2 k 12 ) α 2 n e w = ( k 11 + k 22 − 2 k 12 ) α 2 + y 2 ( f ( x 1 ) − y 1 − f ( x 2 ) + y 2 ) ) (k_{11}+k_{22}-2k_{12})\alpha_{2_{new}}=(k_{11}+k_{22}-2k_{12})\alpha_{2}+y_{2}(f(x_{1})-y_{1}-f(x_{2})+y_{2})) (k11+k22−2k12)α2new=(k11+k22−2k12)α2+y2(f(x1)−y1−f(x2)+y2)) (5)
令 η = k 11 + k 22 − 2 k 12 , E i = f ( x i ) − y i \eta=k_{11}+k_{22}-2k_{12},E_{i}=f(x_{i})-y_{i} η=k11+k22−2k12,Ei=f(xi)−yi并代入公式(5)得:
α 2 n e w = α 2 + y 2 ( E 1 − E 2 ) η \alpha_{2_{new}}=\alpha_{2}+\frac{y_{2}(E_{1}-E_{2})}{\eta} α2new=α2+ηy2(E1−E2)
4、由于 0 ≤ α 1 ≤ C , 0 ≤ α 2 ≤ C 0≤\alpha_{1}≤C,0≤\alpha_{2}≤C 0≤α1≤C,0≤α2≤C,且 α 1 y 1 + α 2 y 2 = c \alpha_{1}y_{1}+\alpha_{2}y_{2}=c α1y1+α2y2=c,所以\alpha_{2_{new}}必落在如下区域内
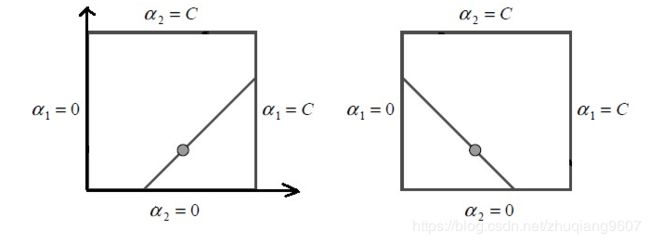
结合图形可以得到 α 2 \alpha_{2} α2的范围:
{ L = m a x { 0 , α 1 + α 2 − C } , H = m i n { C , α 1 + α 2 } , i f y 1 = y 2 L = m a x { 0 , α 2 − α 1 } , H = m i n { C , C + α 2 − α 1 } , i f y 1 ≠ y 2 \left\{\begin{matrix}L=max\left \{ 0,\alpha_{1}+\alpha_{2}-C \right \}, H=min\left \{ C,\alpha_{1}+\alpha_{2}\right \},\: \: \: \: if\: y_{1}=y_{2} \\ L=max\left \{ 0,\alpha_{2}-\alpha_{1} \right \}, H=min\left \{ C,C+\alpha_{2}-\alpha_{1}\right \}, \: \: \: \: if\: y_{1}≠y_{2} \end{matrix}\right. {L=max{0,α1+α2−C},H=min{C,α1+α2},ify1=y2L=max{0,α2−α1},H=min{C,C+α2−α1},ify1̸=y2
此时 α 2 n e w \alpha_{2_{new}} α2new取值为:
α 2 n e w = { H , i f α 2 n e w ≥ H α 2 n e w , i f L < α 2 n e w < H L , i f α 2 n e w ≤ L \alpha_{2_{new}}=\left\{\begin{matrix}H\: \: , \: \: \: \: if\: \alpha_{2_{new}}≥H\: \: \: \: \: \\ \alpha_{2_{new}} , \: \: \: \: if\: L<\alpha_{2_{new}}<H \\ L\: \: , \: \: \: \: if\: \alpha_{2_{new}}≤L\: \: \: \: \: \end{matrix}\right. α2new=⎩⎨⎧H,ifα2new≥Hα2new,ifL<α2new<HL,ifα2new≤L
第三步:重复第一、第二步直到 α i n e w \alpha_{i_{new}} αinew收敛
1、由 α i n e w \alpha_{i_{new}} αinew,根据公式 w = ∑ i = 1 m α i y i x i 求 出 w w=\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i}求出w w=∑i=1mαiyixi求出w
2、只有支持向量满足 1 − y i ( w T x i + b ) = 0 1-y_{i}(w^{T}x_{i}+b)=0 1−yi(wTxi+b)=0,所以大于0的 α i n e w \alpha_{i_{new}} αinew必然都是支持向量,否则 α i n e w > 0 , 1 − y i ( w T x i + b ) < 0 \alpha_{i_{new}}>0,1-y_{i}(w^{T}x_{i}+b)<0 αinew>0,1−yi(wTxi+b)<0,则 α i n e w ( 1 − y i ( w T x i + b ) ) < 0 \alpha_{i_{new}}(1-y_{i}(w^{T}x_{i}+b))<0 αinew(1−yi(wTxi+b))<0与条件 α i n e w ( 1 − y i ( w T x i + b ) ) = 0 \alpha_{i_{new}}(1-y_{i}(w^{T}x_{i}+b))=0 αinew(1−yi(wTxi+b))=0(KKT条件)相违背
3、现实中采用了一种鲁棒的方法求解b,方式为:
b = 1 ∣ S ∣ ∑ s ∈ S ( 1 y s − w x s ) b=\frac{1}{|S|}\sum_{s∈S}(\frac{1}{y_{s}}-wx_s) b=∣S∣1∑s∈S(ys1−wxs)
4、最终超平面为:
w x + b = 0 wx+b=0 wx+b=0
根据分类决策函数 f ( x ) = s i g n ( w x + b ) f(x)=sign(wx+b) f(x)=sign(wx+b)得:
s i g n ( x ) = { − 1 , i f x < 0 0 , i f x = 0 1 , i f x > 0 sign(x)=\left\{\begin{matrix}-1\: , \: \: if\: x<0 \\\: \: \: \: \: 0\: ,\: \: if\:x=0\: \\ \: \: \: \: \: 1\:,\: \: if\: x>0\: \end{matrix}\right. sign(x)=⎩⎨⎧−1,ifx<00,ifx=01,ifx>0