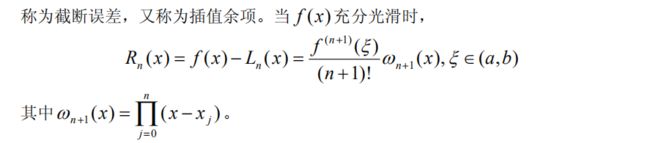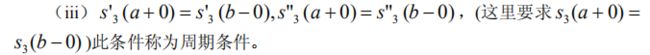《数学建模算法与应用》——学习笔记chapter9. 插值与拟合

插值：求过已知有限个数据点的近似函数。
拟合：已知有限个数据点，求近似函数，不要求过已知数据点，只要求在某种意义下它在这些点上的总偏差最小。

1. 插值方法

基本的、常用的插值：拉格朗日多项式插值、牛顿插值、分段线性插值、Hermite 插值和三次样条插值。

1.1 拉格朗日多项式插值

1.1.1 插值多项式

1.1.2 拉格朗日插值多项式

1.1.3 用 Matlab 作 Lagrange 插值

设n 个节点数据以数组 x0, y0输入（注意 MatlaB 的数组下标从 1 开始），m 个插值点以数组 x 输入，输出数组 y 为m 个插值。编写一个名为 lagrange.m 的 M 文件：

function y=lagrange(x0,y0,x); 
n=length(x0);m=length(x); 
for i=1:m 
	z=x(i); 
	s=0.0; 
	for k=1:n 
		p=1.0; 
		for j=1:n 
			if j~=k 
				p=p*(z-x0(j))/(x0(k)-x0(j)); 
			end 
		end 
		s=p*y0(k)+s; 
	end 
	y(i)=s; 
end

1.2 牛顿（Newton）插值

1.2.1 差商

1.2.2 Newton 插值公式

1.2.3 差分

1.2.4 等距节点插值公式

1.3 分段线性插值

1.3.1 插值多项式的振荡

用 Lagrange 插值多项式 L (x) n 近似 f (x)(a ≤ x ≤ b) ，虽然随着节点个数的增加，$L_n(x)$的次数n 变大，多数情况下误差$|R_n(x)|$ 会变小。但是n 增大时，$L_n(x)$的光滑性变坏，有时会出现很大的振荡。理论上，当n →∞，在[a,b]内并不能保证$L_n(x)$处处收敛于 f (x)。

高次插值多项式的这些缺陷，促使人们转而寻求简单的低次多项式插值。

1.3.2 分段线性插值

将每两个相邻的节点用直线连起来，如此形成的一条折线就是分段线性插值函数，记作$I_n(x)$。

用$I_n(x)$计算 x 点的插值时，只用到x左右的两个节点，计算量与节点个数n 无关。但n 越大，分段越多，插值误差越小。实际上用函数表作插值计算时，分段线性插值就足够了，如数学、物理中用的特殊函数表，数理统计中用的概率分布表等。

1.3.3 用 Matlab 实现分段线性插值

Matlab 中有现成的一维插值函数 interp1：y=interp1(x0,y0,x,‘method’)

method 指定插值的方法，默认为线性插值。其值可为：
‘nearest’ 最近项插值
‘linear’ 线性插值
‘spline’ 逐段 3 次样条插值
‘cubic’ 保凹凸性 3 次插值。
所有的插值方法要求 x0 是单调的。
当 x0 为等距时可以用快速插值法，使用快速插值法的格式为’*nearest’、’*linear’、’*spline’、’*cubic’。

1.4 埃尔米特(Hermite)插值

1.4.1 Hermite 插值多项式

如果对插值函数，不仅要求它在节点处与函数同值，而且要求它与函数有相同的一阶、二阶甚至更高阶的导数值，这就是 Hermite 插值问题。

Hermite 插值多项式为

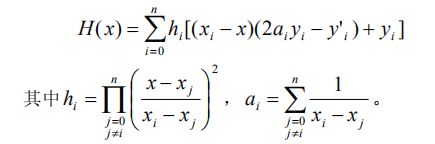
1.4.2 用 Matlab 实现 Hermite 插值

设n个节点的数据以数组 x0（已知点的横坐标），y0（函数值），y1（导数值）输入（注意 Matlab 的数组下标从 1 开始），m个插值点以数组 x 输入，输出数组 y 为m个插值。编写一个名为 hermite.m 的 M 文件：

function y=hermite(x0,y0,y1,x); 
n=length(x0);m=length(x); 
for k=1:m 
	yy=0.0; 
	for i=1:n 
		h=1.0; 
		a=0.0; 
		for j=1:n 
			if j~=i 
				h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2; 
				a=1/(x0(i)-x0(j))+a; 
			end 
		end 
		yy=yy+h*((x0(i)-x(k))*(2*a*y0(i)-y1(i))+y0(i)); 
	end 
y(k)=yy; 
end

1.5 样条插值

1.5.1 样条函数的概念

1.5.2 二次样条函数插值

1.5.3 三次样条函数插值

1.5.4 三次样条插值在 Matlab 中的实现

Matlab 中三次样条插值也有现成的函数：
y=interp1(x0,y0,x,‘spline’)；
y=spline(x0,y0,x)；
pp=csape(x0,y0,conds)，y=ppval(pp,x)。
其中 x0,y0 是已知数据点，x 是插值点，y 是插值点的函数值。

对于三次样条插值，我们提倡使用函数 csape，csape 的返回值是 pp 形式，要求插值点的函数值，必须调用函数 ppval。
pp=csape(x0,y0)：使用默认的边界条件，即 Lagrange 边界条件。
pp=csape(x0,y0,conds)中的 conds 指定插值的边界条件，其值可为：
‘complete’ 边界为一阶导数，即默认的边界条件
‘not-a-knot’ 非扭结条件
‘periodic’ 周期条件
‘second’ 边界为二阶导数，二阶导数的值[0, 0]。
‘variational’ 设置边界的二阶导数值为[0,0]。

对于一些特殊的边界条件，可以通过 conds 的一个1×2 矩阵来表示，conds 元素的取值为 1，2。此时，使用命令

pp=csape(x0,y0_ext,conds)

其中 y0_ext=[left, y0, right]，这里 left 表示左边界的取值，right 表示右边界的取值。conds(i)=j 的含义是给定端点i 的 j 阶导数，即 conds 的第一个元素表示左边界的条件，第二个元素表示右边界的条件，conds=[2,1]表示左边界是二阶导数，右边界是一阶导数，对应的值由 left 和 right 给出。

1.6 B 样条函数插值方法

1.6.1 磨光函数

实际中的许多问题，往往是既要求近似函数（曲线或曲面）有足够的光滑性，又要求与实际函数有相同的凹凸性，一般插值函数和样条函数都不具有这种性质。如果对于一个特殊函数进行磨光处理生成磨光函数（多项式），则用磨光函数构造出样条函数作为插值函数，既有足够的光滑性，而且也具有较好的保凹凸性，因此磨光函数在一维插值（曲线）和二维插值（曲面）问题中有着广泛的应用。

由积分理论可知，对于可积函数通过积分会提高函数的光滑度，因此，我们可以利用积分方法对函数进行磨光处理。

1.6.2 等距 B 样条函数

对于任意的函数 f (x) ，定义其步长为 1 的中心差分算子δ 如下：

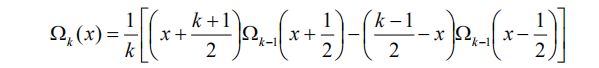
1.6.3 一维等距 B 样条函数插值

1.6.4 二维等距 B 样条函数插值

1.7 二维插值

1.7.1 插值节点为网格节点

Matlab 中有一些计算二维插值的程序。如
z=interp2(x0,y0,z0,x,y,‘method’)
其中 x0,y0 分别为m 维和n 维向量，表示节点，z0 为n × m 维矩阵，表示节点值，x,y为一维数组，表示插值点，x 与 y 应是方向不同的向量，即一个是行向量，另一个是列向量，z为矩阵，它的行数为y的维数，列数为x的维数，表示得到的插值，‘method’
的用法同上面的一维插值。

如果是三次样条插值，可以使用命令
pp=csape({x0,y0},z0,conds,valconds)，z=fnval(pp,{x,y})
其中 x0,y0 分别为m 维和n 维向量，z0 为m × n 维矩阵，z 为矩阵，它的行数为 x 维数，列数为 y 的维数，表示得到的插值，具体使用方法同一维插值。

1.7.2 插值节点为散乱节点

ZI = GRIDDATA(X,Y,Z,XI,YI)
其中 X、Y、Z 均为 n 维向量，指明所给数据点的横坐标、纵坐标和竖坐标。向量XI、YI 是给定的网格点的横坐标和纵坐标，返回值 ZI 为网格（XI，YI）处的函数值。XI与 YI 应是方向不同的向量，即一个是行向量，另一个是列向量。

2. 曲线拟合的线性最小二乘法

2.1 线性最小二乘法

曲线拟合问题的提法是，已知一组（二维）数据，即平面上的n 个点互不相同，寻求一个函数（曲线）y = f (x) ，使 f (x)在某种准则下与所有数据点最为接近，即曲线拟合得最好。

2.1.1 系数$a_k$的确定

如果通过机理分析，能够知道 y 与 x 之间应该有什么样的函数关系，则$r_1(x),...r_m(x)$容易确定。若无法知道 y 与 x 之间的关系，通常可以将数据$(x_i,y_i)$作图，直观地判断应该用什么样的曲线去作拟合。人们常用的曲线有
（i）直线
（ii）多项式
（iii）双曲线（一支）
（iv）指数曲线

2.2 最小二乘法的 Matlab 实现

2.2.1 解方程组方法

2.2.2 多项式拟合方法

3. 最小二乘优化

无约束最优化问题中，有些目标函数由若干个函数的平方和构成，把极小化这类函数的问题称为最小二乘优化问题。

3.1 lsqlin 函数

3.2 lsqcurvefit 函数

3.3 lsqnonlin 函数

3.4 lsqnonneg 函数

3.5 曲线拟合的用户图形界面求法

Matlab 工具箱提供了命令 cftool，该命令给出了一维数据拟合的交互式环境。具体执行步骤如下：
（1）把数据导入到工作空间；
（2）运行 cftool，打开用户图形界面窗口；
（3）对数据进行预处理；
（4）选择适当的模型进行拟合；
（5）生成一些相关的统计量，并进行预测。

4. 曲线拟合与函数逼近

已知一个较为复杂的连续函数 y(x), x ∈[a,b]，要求选择一个较简单的函数f (x)，在一定准则下最接近 f (x)，就是所谓函数逼近。