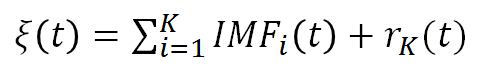EMD算法之Hilbert-Huang Transform原理详解和案例分析

本分享为脑机学习者Rose整理发表于公众号：脑机接口社区(微信号：Brain_Computer).QQ交流群：941473018

Hilbert-Huang Transform 希尔伯特-黄变换

在我们正式开始讲解Hilbert-Huang Transform之前，不妨先来了解一下这一伟大算法的两位发明人和这一算法的应用领域。

Section I 人物简介

希尔伯特：公认的数学界“无冕之王”，1943年去世于瑞士苏黎世。除此之外，自不必过多介绍。

黄锷：1937年出生于湖北省；1975年进入NASA（美国国家宇航局）；美国国家工程院院士。

Section II Hilbert-Huang的应用领域

医学领域：探测心率不齐、登革热的扩散、血压的变化
　　交通领域：探测公路桥梁安全
　　安全领域：辨识发言者的身份
　　地理领域：地震工程
　　航天领域：卫星资料分析

在了解了这一伟大发明的背景后，下面我们要正式的开始入手希尔伯特-黄变换了，我将尝试以尽可能简要的语言向大家介绍这一发明，并尽可能的避免不必要的数学推导。

Section III Hilbert-Huang的算法详细介绍

如下图所示，在希尔伯特-黄的运算步骤中，原始脑电信号/其他时序信号被作为Huang的算法的输入，在经过huang的算法处理过后被当做Hilbert的输入进行处理。这便是Hilbert-Huang最简单明了的运算步骤。在这里为了继续往下的讲解更加方便，我们先来介绍两个概念。上文中，我们提到了“huang的算法”，在正式的书面语言中，我们并不这么称呼它，而是将“huang的算法”称为EMD(Empirical mode decomposition,经验模式分解)。而另外一个概念IMF在这里直接讲解或许会使大家晕头转向（或许有人注意到图中的IMF后面有一个‘s’，而这里却没有加‘s’，对英语只有基础了解的人也应猜到IMF不止一个）。

当讲到这里的时候，大部分人或许会萌生出一个念头----“难道Huang仅仅是对Hilbert的锦上添花吗”。好吧，至少本人当初就是这样想的，毕竟Hilbert比huang更早出名，而且Hilbert是数学史上公认的“大牛”，哦，不对，是“大王”。用当前时兴的话来说就是“huang有可能抱了Hilbert的大腿”。但当我真正了解了这一伟大的发明之后，我才彻彻底底打消了这个十分愚蠢的念头。

我个人并不喜欢吊人胃口，这里把结论说在前面“Huang的算法几乎是Hilbert使用的前提条件，Hilbert Transform则是Hilbert-Huang算法的精要所在”（注意句中出现了“几乎”一词）。

下面我就给大家讲一下这句话的由来。比如我们造了一款叫做“榔头”的手机，“榔头”手机对用户的使用提出了下列要求：1.晚上不能使用。2.下雨天不能打。3.室内不能打。4.室外的偏远郊区也不能打。

实际上，Hilbert正是这样一款“榔头”手机，它对用户的使用提出了近乎苛刻的要求。Hilbert变换算法要求输入信号只能是线性稳态的。请注意这里是两个词“线性”“稳态”。无论是在自然界还是在人类社会中，绝大部分的信号要么是“线性非稳态”，要么是“非线性稳态”，要么干脆是“非线性非稳态”。我们关心的重点----EEG信号正是这样一类“非线性非稳态”的信号。这也就导致了绝大部分信号不能够愉快的进入Hilbert的“碗里”来。此时，Huang的EMD算法起到了这样的作用，它能够将所有的时域信号转化为“线性稳态”，解了Hilbert算法的软肋。

首先，我们先说一说Huang的EMD算法。为了讲解清晰起见，我将对照下图予以讲解：

上图中，深蓝色的线条是EEG信号（截取自瑞士联邦理工学院DEAP数据库 s01 trail1 channel1的前200个数据点）。图中，红线上的红点是该EEG signal的极大值点，绿线上的绿点是该signal的极小值点。

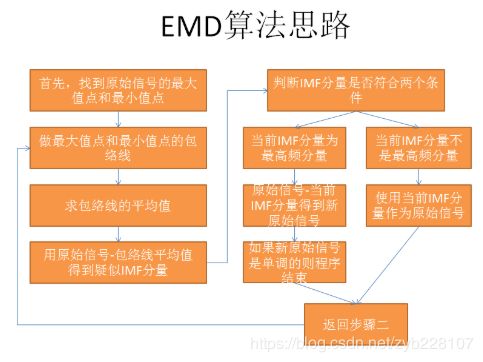
我们分别为极大值点和极小值点做三次包络线做好的包络线分别是红色包络线和绿色包络线两条线。为这两条线做出均值线即为图中围绕y=0轴（注意y=0轴的位置，并非是图中的坐标系的x轴，x轴所代表的线是y=-10）震荡的浅蓝色均值线。之后，我们将原始EEG信号减去均值线，得到疑似IMF线（图中未标出）（这里终于出现IMF了，可是我还是无法让你直观理解，大家先暂且忍忍，强行记忆一下）。之后，我们对疑似IMF进行判断（需要同时满足两个条件，下面讲）。如果满足条件，则疑似IMF升级为正式IMF。然后将原始信号减去正式IMF的结果赋值给原始信号，说白了就是让这一IMF从原始信号里“滚蛋”。就好比蒙面歌王的某一期的获胜者一样，都赢了，不滚干嘛，难道还要和加时赛选手（减完后剩下的原始信号，也即新原始信号）在一起吗？另一个方面，如果疑似IMF未能通过检验，则将当前IMF作为原始信号，并回到做极值点的包络线那一步重新开始。现在讲一下两个重要的条件：

条件1：均值线（总得有很多数构成吧）的平均值趋近于0（一般和0做差<0.1）
条件2：原始信号的极值点个数（包括极大值点个数+极小值点个数）和原始信号同y=0的交点个数之差不能大于1（小于等于1）

那么这样一个程序什么时候可以循环结束呢，答案是，当某一次IMF被发现是单调函数或者是缺少极大/小值点即可让程序结束。下图是程序流程图。

空口无凭，我们处理一段真正的脑电试试看（程序会在之后给出）

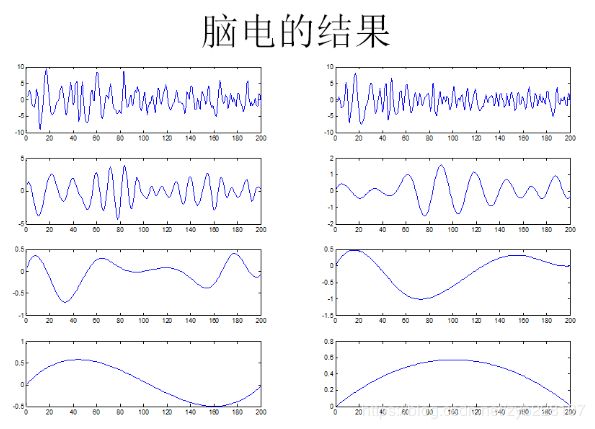
图中共有4*2个图，位于（1,1）这个位置的是脑电的原始信号。之后从（1,2）->(4,2)均为IMF。其中，除了（1,1）自身，每一副图都是（1,1）的一个IMF（现在知道什么是IMF了吧）。通过观察不难发现。一个典型的IMF分量的上下包络线肯定是对称的。最后一个IMF（4,2）被称为余项用r表示。观察即可知该IMF分量没有极小值点（端点除外），所以程序才会结束。通常来讲，别的书上会这样用数学公式告诉你：

其中ξ(t)就是原始信号，IMFi就是K个固有模态函数。rK就是原始信号减完IMF后剩下的余项。

下面是求解EMD算法的Matlab源程序。

%非主函数，被调用
function n = findpeaks(x)%用于寻找极值点，该函数只会求极大值
%   Find peaks.
%   n = findpeaks(x)
    n = find(diff(diff(x)>0)<0);%一阶导数大于0二阶导数小于0的点
    u = find(x(n+1)>x(n));
    n(u) = n(u) + 1;
end

%非主函数，被调用<br>%判断x是否单调，返回0代表不是单调，返回1代表是单调
function u = ismonotonic(x)
    u1 = length(findpeaks(x))*length(findpeaks(-x));%如果最大/最小值有一个为0即可判断程序满足退出条件了
    if u1 > 0
        u = 0;
    else
        u = 1;
    end
end

%非主函数，被调用。判断当前x是不是真IMF
function u = isimf(x)
    N  = length(x);
    u1 = sum(x(1:N-1).*x(2:N) < 0);%求x与y=0轴交点的个数
    u2 = length(findpeaks(x))+length(findpeaks(-x));%求极值点个数
    if abs(u1-u2) > 1
        u = 0;
    else
        u = 1;
    end
end

%非主函数，被调用，作用是获得x的包络线
function s = getspline(x)
    N = length(x);
    p = findpeaks(x);
    s = spline([0 p N+1],[0 x(p) 0],1:N);
end

%主函数
function imf = emd(x)
% Empiricial Mode Decomposition (Hilbert-Huang Transform)
% imf = emd(x)
% Func : findpeaks
    x = transpose(x(:));
    imf = [];
    while ~ismonotonic(x)
        x1 = x;
        sd = Inf;
        while (sd > 0.1) || ~isimf(x1)
            s1 = getspline(x1);
            s2 = -getspline(-x1);
            x2 = x1-(s1+s2)/2;
       
            sd = sum((x1-x2).^2)/sum(x1.^2);
            x1 = x2;
        end
    
        imf(end+1,:) = x1;
        x = x-x1;
    end
    imf(end+1,:) = x;
end

特此声明，本程序为我本人在网上找到的，除了注释外，其他版权皆归属原作者，由于不清楚原作者是谁，未能标出，如果侵犯权利，请联系我删除源码。

Section IV Hilbert算法的介绍

在上一章中，我们介绍了EMD算法，在这一部分中，我会介绍Hilbert算法，这一节有些许数学趣味，对数学趣味不感兴趣的直接跳到应用部分。

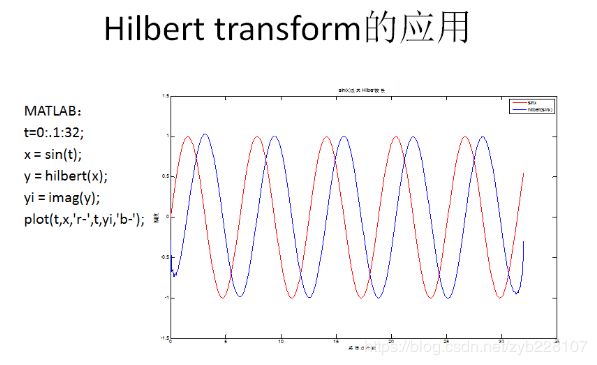
由最后一步可以知道，当频率大于0时，相位向左移90度；反之，向右移90度。这便是希尔伯特变换。

一般来讲，对于原始信号x(t)的希尔伯特变换H[x(t)]，通常被写为

z(t)=x(t)+j H[x(t)]

其中，x(t)被称为复信号z(t)的实部，H[x(t)]被称为复信号z(t)的虚部， z(t)被称为x(t)的解析信号。

一般情况下，matlab会将z(t)给出，而不直接给出原始信号的希尔伯特变换，所以需要使用imag函数求解z(t)的虚部，这才是真正的希尔伯特变换。

这篇文章来源于Mario-Chao的授权转载。
参考：
https://www.cnblogs.com/hdu-zsk/p/4799470.html
EMD算法之Hilbert-Huang Transform原理详解和案例分析
本文章由脑机学习者Rose笔记分享,QQ交流群：941473018
更多分享，请关注公众号