SPSS（六）SPSS之回归分析衍生方法（图文+数据集）
SPSS（六）SPSS之回归分析衍生方法（图文+数据集）
我们知道线性回归是有适用条件的
- 因变量的独立性
- 正态性
- 方差齐性
- 无极端值
- 自变量、因变量要有线性趋势
假如不满足以上的条件，还能做回归分析吗？其实有一大类针对此相关的方法
曲线拟合过程
针对问题：自变量、因变量无线性趋势
- 直线关系毕竟是较少数的情形，当因变量和自变量呈曲线关系时：
有明确的公式：利用变量变换将曲线直线化，然后加以拟合
关系不明：基于图形观察，拟合可能的曲线，从中挑选出最为合适的一个
- 具体拟合方法：根据所选择的公式，将自变量和因变量进行变量变换，然后按照直线回归的方式进行拟合
- 可拟合的曲线种类
高次方曲线：一、二、三次方曲线
指数、对数、幂曲线
特殊类型曲线：S形曲线、生长曲线等
简单来说分两种情况
- 第一种情况：一个是已经给出表达式，我们将其进行变量转换为线性，之后进行回归
- 第二种情况：另一个是我们结合可拟合的曲线种类，看哪一个表达式拟合效果比较好，挑选这个表达式进行线性变换，之后回归
案例：通风时间和毒物浓度的曲线方程（第一种情况）
根据文献资料，随着通风时间的增加，密闭空间内污染物的浓度应当呈指数方程下降。现考察某通风设备的换气效果，在室内放置了某种挥发性物质（模拟毒物），待其充分分散到室内空气中后开始通风，每一分钟测量一次室内空气中的毒物浓度，请建立时间与空气中毒物浓度的指数方程。
（已有明确的方程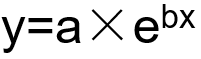
，按此拟合即可。等价于先进行变量变换，然后拟合直线方程）
数据集如下
1 2.1250
2 1.7420
3 1.2360
4 1.1270
5 .7310
6 .4690
7 .4000
8 .3810
9 .2840
10 .2760
11 .0620
12 .0610
13 .0408
14 .0428
15 .0305首先进行变量变化（转换----计算变量）
建一个新变量，对原始的y进行ln运算，使之ln（y）与x成线性关系
建模
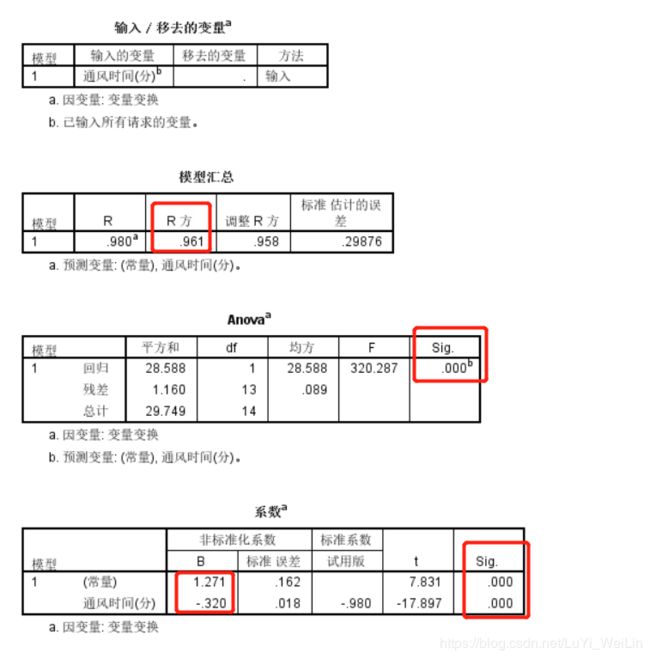
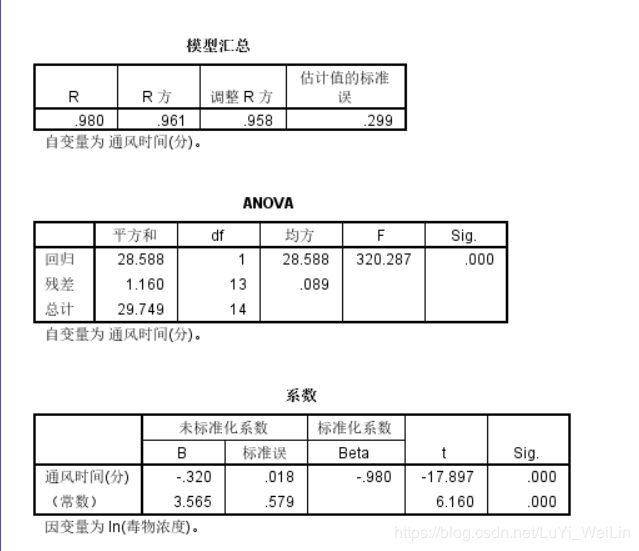
结果查看，一般我们只关注和几个地方
R方：决定系数，衡量模型可用性及模型信息量的表达，越接近1越好
Anova：里面的Sig.表示lny与x解决问题使用线性回归模型是否可行的
系数a：Sig.这个因变量纳入这个模型有没有意义
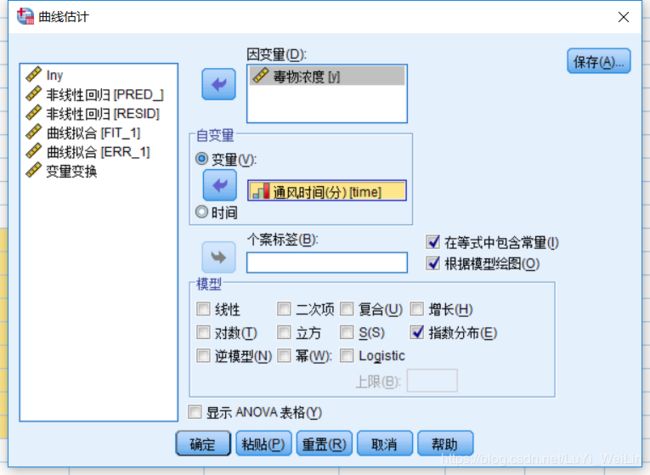
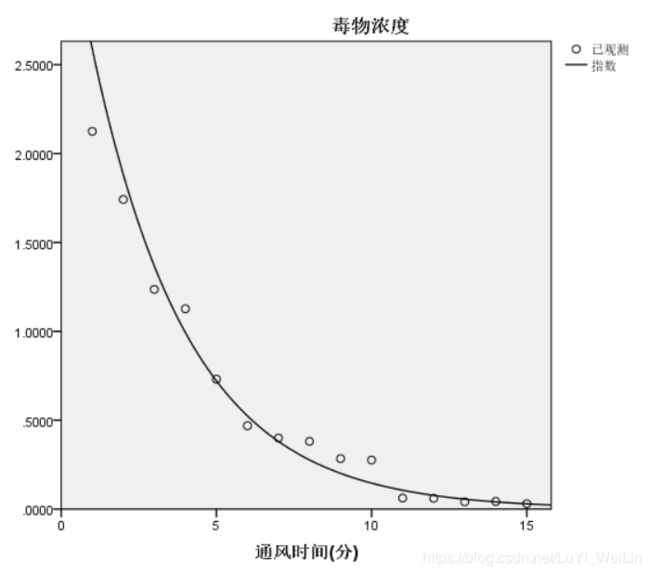
还有一个比较快的方法，不用计算出新的变量（分析----回归----曲线估计）
结果和刚才线性回归查看方法差不多
不过有图形展现出来
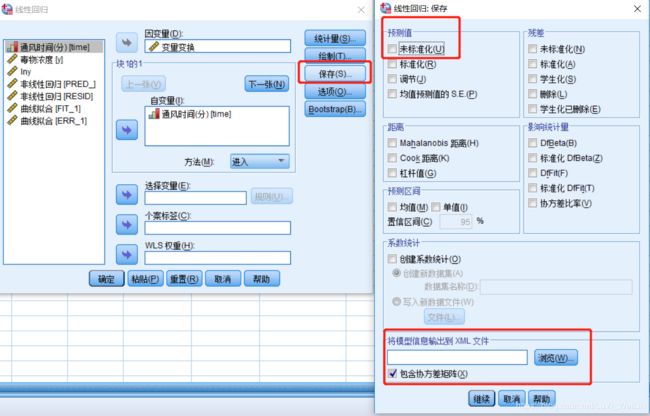
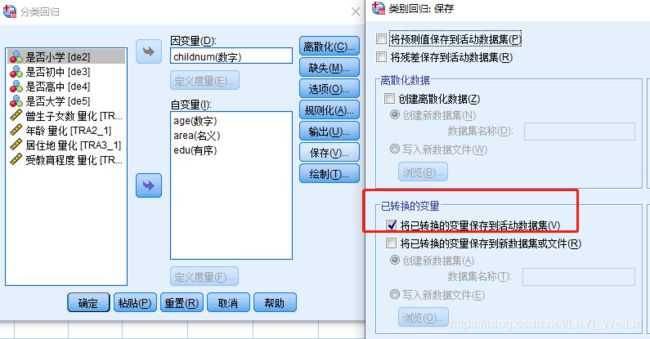
线性回归想保存预测值方法
- 保存--预测值
- 将模型信息输出到XML文件
加权最小二乘法
加权最小二乘法是对原模型进行加权，使之成为一个新的不存在异方差性的模型，然后采用普通最小二乘法估计其参数的一种数学优化技术。
针对问题：方差齐性不齐
一般我们如何发现线性回归的方差齐性不齐的呢，一般是在做残差分析的时候，假如我们遇到的标准化残差图如下（残差随着自变量的变大而增大或者随着自变量的变大而减小，就证明有问题）
- 因变量的变异随着某些指标的改变而改变（下面的例子）
1.以地区为观察单位调查某种事物的发生率
2.研究通货膨胀和失业率对股票价格的影响
高价股票的波动一般都会大于低价股票
针对这种问题解决办法
需要人为调控各案例在回归中的重要性，根据用户提供的可能预测因变量变异大小的指标，在拟合时对变异较小（即测量更精确）的测量值赋予较大的权重（现实生活中也会有反过来的情况）
为了解决上述数据分析的问题，SPSS专门提供了加权最小二乘法，它可根据用户提供的权重变量的大小为不同的数据不同权重。需要指出的是，加权最小二乘法是一种带有倾向性的数据拟合方法，如果因变量方差实际并无波动，或选择了错误的变量用于权重，那么它的拟合结果不如普通最小二乘法准确。
案例：不等量样品数据的回归方程
实验中收集得15对数据，每对数据都是将n份样品混合后测得的平均结果，但各对数据的n大小不等，试求出X对Y的直线回归方程
2 188 4.90
3 195 4.58
11 207 4.40
16 217 4.18
18 224 3.90
19 236 3.85
20 246 3.77
22 255 3.54
18 266 3.47
15 275 3.34
12 285 3.19
5 295 3.08
5 312 2.94
4 320 2.79
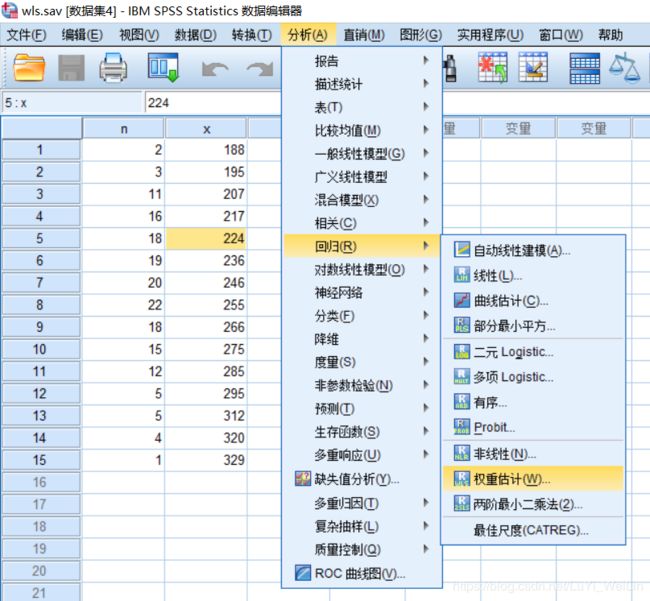
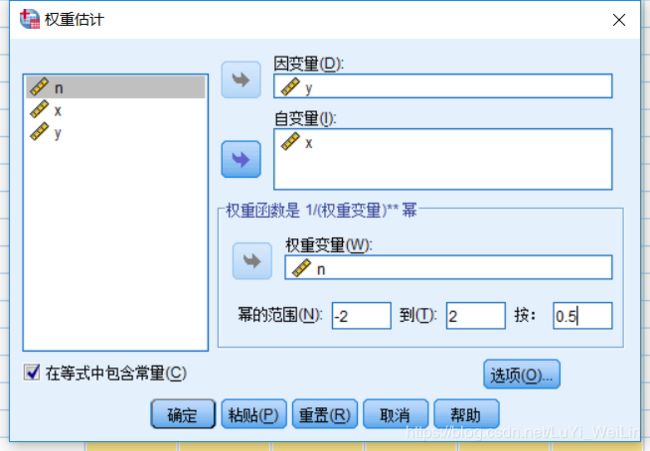
1 329 2.49分析----回归----权重估计
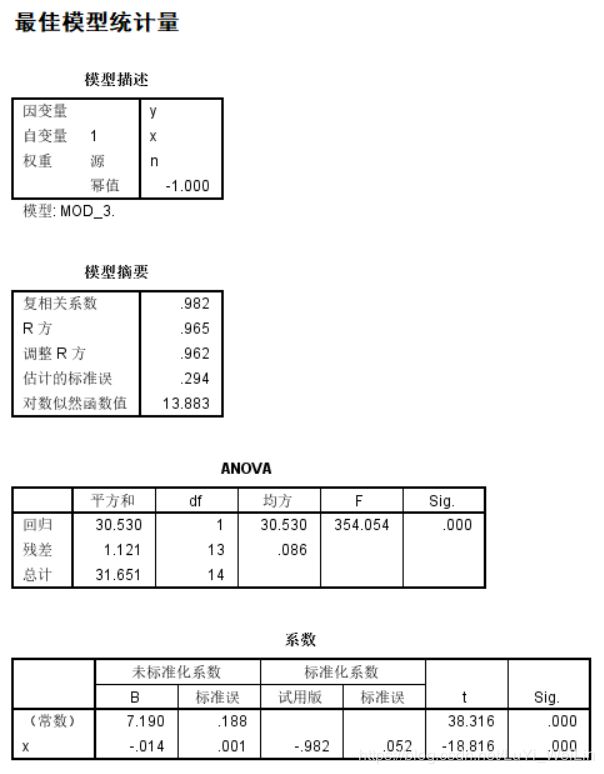
结果如下
对数似然值越大代表这个模型越好
加权后的决定系数基本上都是低于原模型的，其他结果和线性回归的结果解读一样
岭回归
针对问题：数据存在共线性，非独立
岭回归是一种专门用于共线性数据分析的有偏估计方法
§有偏意味着对数据信息有所取舍
§通过丢弃部分信息，以得到更为稳定的分析结果
§实际上是一种改良的最小二乘法
§由于是有偏估计，统计检验已经居次要地位，故一般不再给出
案例：用外形指标推测胎儿周龄
现测得22例胎儿的身长、头围、体重和胎儿受精周龄，研究者希望能建立由前三个外形指标推测胎儿周龄的回归方程
数据集如下
1.00 13.00 9.20 50.00 13.00
2.00 18.70 13.20 102.00 14.00
3.00 21.00 14.80 150.00 15.00
4.00 19.00 13.30 110.00 16.00
5.00 22.80 16.00 200.00 17.00
6.00 26.00 18.20 330.00 18.00
7.00 28.00 19.70 450.00 19.00
8.00 31.40 22.50 450.00 20.00
9.00 30.30 21.40 550.00 21.00
10.00 29.20 20.50 640.00 22.00
11.00 36.20 25.20 800.00 23.00
12.00 37.00 26.10 1090.00 24.00
13.00 37.90 27.20 1140.00 25.00
14.00 41.60 30.00 1500.00 26.00
15.00 38.20 27.10 1180.00 27.00
16.00 39.40 27.40 1320.00 28.00
17.00 39.20 27.60 1400.00 29.00
18.00 42.00 29.40 1600.00 30.00
19.00 43.00 30.00 1600.00 31.00
20.00 41.10 27.20 1400.00 33.00
21.00 43.00 31.00 2050.00 35.00
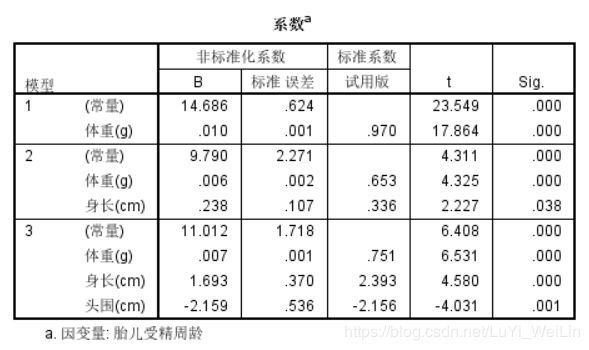
22.00 49.00 34.80 2500.00 36.00我们在不做任何修正的情况下，把所有自变量和因变量放入模型进行线性回归
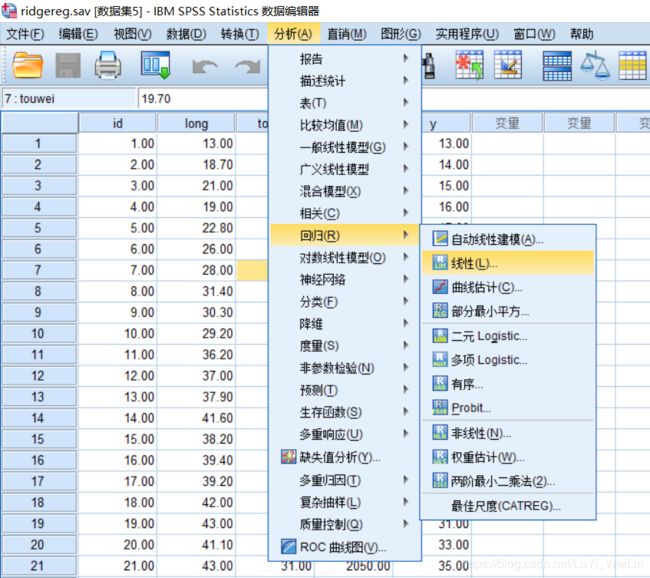
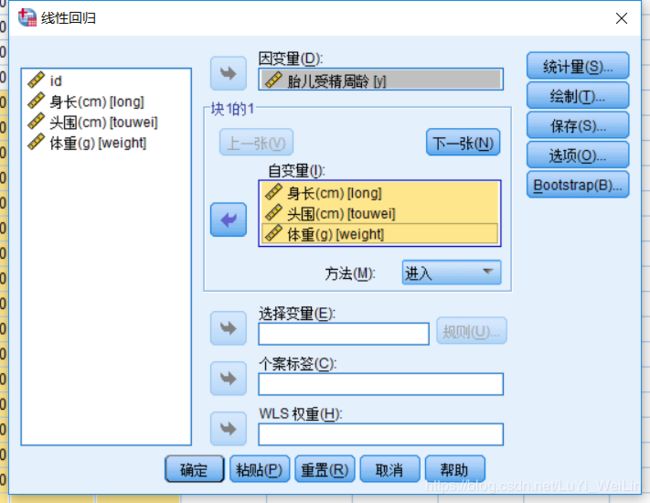
分析----回归----线性
发现结果逻辑上解释不上来，在身长和体重不变的情况下，受精周龄增加一岁头围会减少2.159cm，这个解释不通，所以我们考虑是不是没有把所有变量都纳入的需要，是不是有变量没有意义，我们下一步使用逐步回归模型，观察结果
使用向前法、向后法、逐步法观看结果
向前法结果
向后法结果
逐步法结果
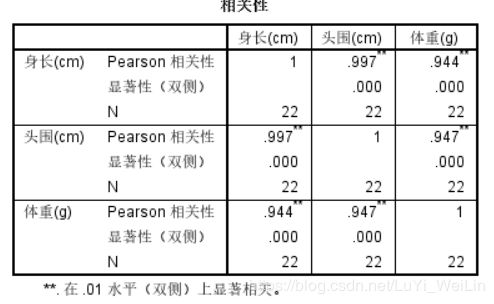
发现逐步回归模型也不能解决我们的问题，我们先来查看一下变量之间的相关性
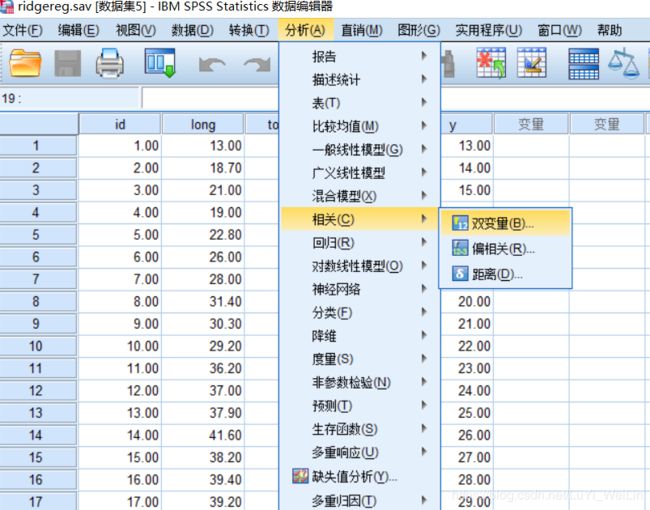
分析----相关----双变量
发现变量之间显著相关，现在使用岭回归来解决回归问题
岭回归分析在SPSS中没有可供点击的对话框，我们需要写一段超级简单的语法来调用SPSS的宏。
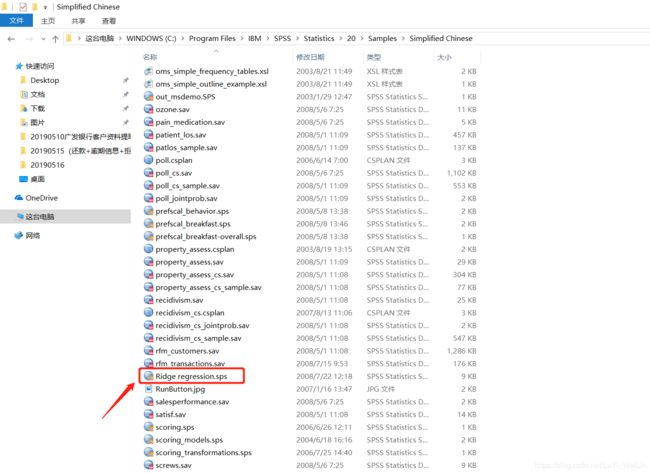
SPSS公司可能没有提供人机交互的对话框，于是他们提供了一段宏程序，存储路径为“你的SPSS安装目录\SPSS\Statistics\20\Samples\Simplified Chinese\Ridge regression.sps”。
我们在SPPS中，点击打开新建语法
输入代码之后执行
INCLUDE 'C:\Program Files\IBM\SPSS\Statistics\20\Samples\Simplified Chinese\Ridge Regression.sps'.
RIDGEREG ENTER= long touwei weight
/dep = y
/ inc = 0.01 .
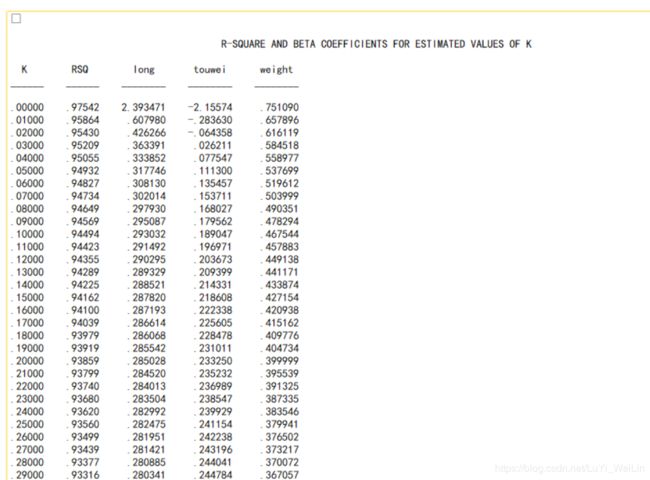
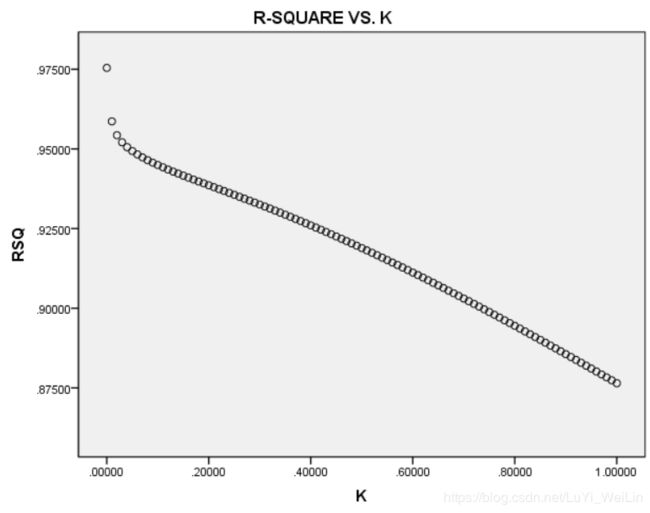
查看结果1、不同K值下自变量的标准化回归系数；2、岭轨图，3、R方的变化图。
随着K的增大可以理解为我们在舍弃更多的信息，RSQ随着K的增大而减少，证明模型信息量在损失，后面为三个系数在变化，找其稳定值
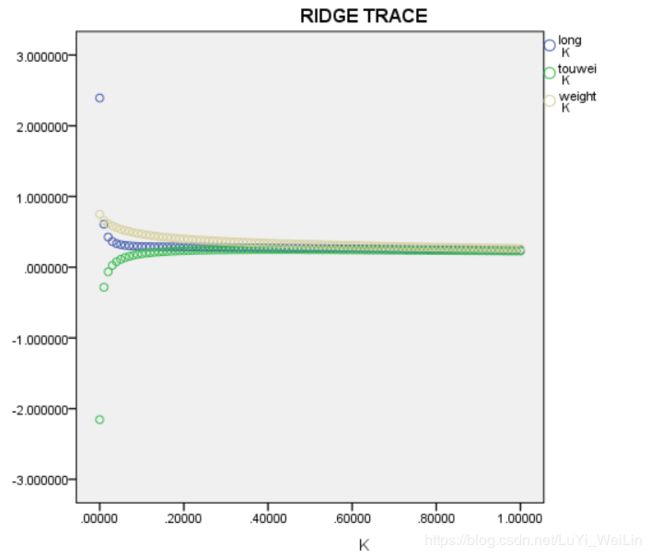
查看岭迹图找到合适K值
选择一定K值下的标准化回归系数，选择的原则是各个自变量的标准化回归系数趋于稳定时的最小K值。因为K值越小我们引入的单位矩阵就少，偏差就小。
想获得非标准的偏回归系数、t值和p值呢（可以参考下面这篇文章链接）
http://www.ttdoc.cn/article/572.jhtml
完整的岭回归分析做完了，各个自变量的标准化回归系数合理了
假如我们研究的问题只是做预测，看模型的决定系数，发现其很高，其实可以忽略共线性问题，直接用来预测即可
但是假如我们要看自变量的影响，就必须解决变量之间的共线性
最优尺度回归
样本量大结果才稳定，灵敏度高，当样本少的时候结果不稳定
针对问题：当自变量为有序/无序的变量
解决办法：根据数据情况进行迭代搜索，找到适当的变换方法对原始分类变量进行转换，将原始变量一律转换为连续性评分，然后再进行方程拟合，分类变量越多优势越明显，从实用的角度出发，该方法可以被作为一种探索性方法使用
案例：生育子女数的回归模型
现收集了一批妇女的曾生子女数、年龄、居住地类别（1：城市，2：农村）、受教育程度（1~5分别代表文盲半文盲、小学、初中、高中、大学及以上），请建立后三个变量对曾生子女数的回归模型
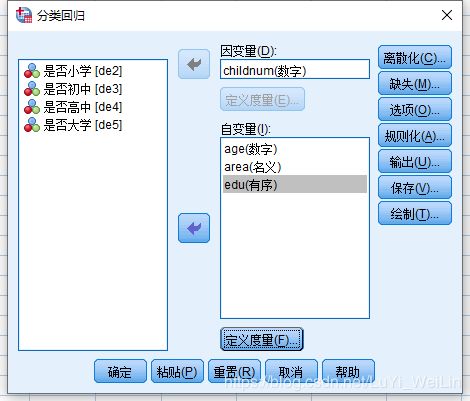
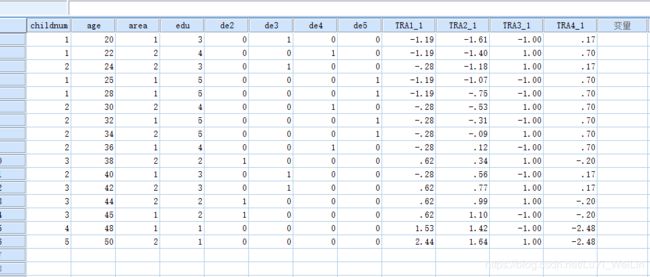
红框是教育程度的哑变量编码，我们可以直接利用childnum与age、area、四个哑变量进行线性回归建模（分析--回归--线性），但是我们现在利用系统把edu变量转换成连续性
1 20 1 3 0 1 0 0
1 22 2 4 0 0 1 0
2 24 2 3 0 1 0 0
1 25 1 5 0 0 0 1
1 28 1 5 0 0 0 1
2 30 2 4 0 0 1 0
2 32 1 5 0 0 0 1
2 34 2 5 0 0 0 1
2 36 1 4 0 0 1 0
3 38 2 2 1 0 0 0
2 40 1 3 0 1 0 0
3 42 2 3 0 1 0 0
3 44 2 2 1 0 0 0
3 45 1 2 1 0 0 0
4 48 1 1 0 0 0 0
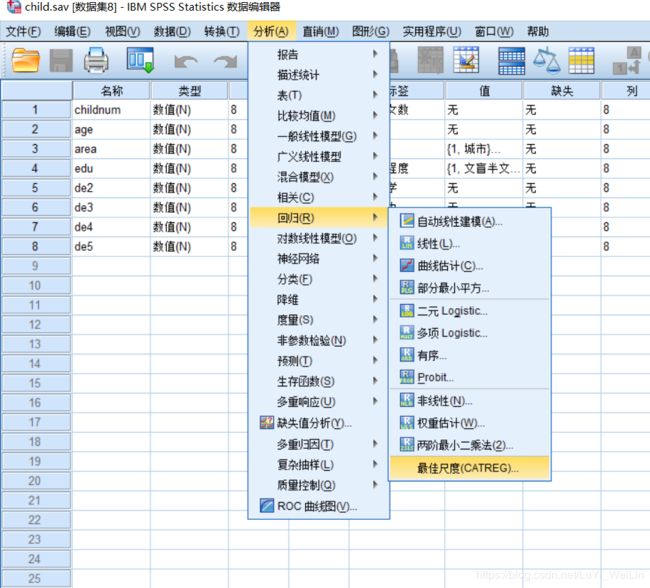
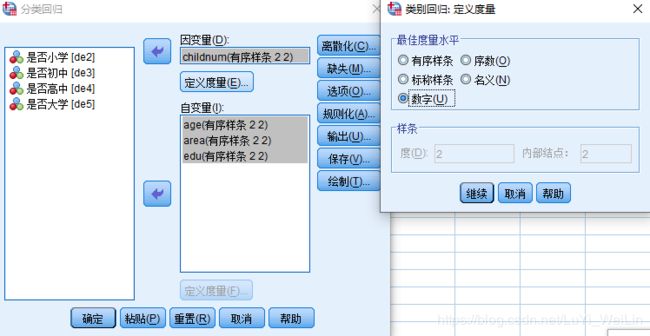
5 50 2 1 0 0 0 0建模（分析--回归--最佳尺度）
定义变量度量
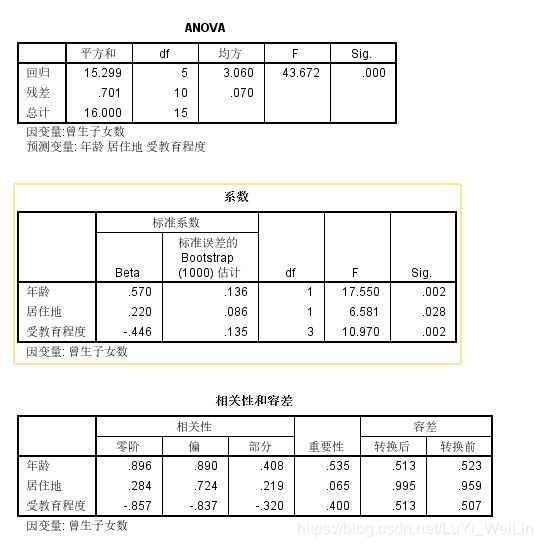
结果如下
R2用来衡量模型的可用性
系数里面有回归的系数
主要看相关性和容差，重要性其实有点类似标化回归系数
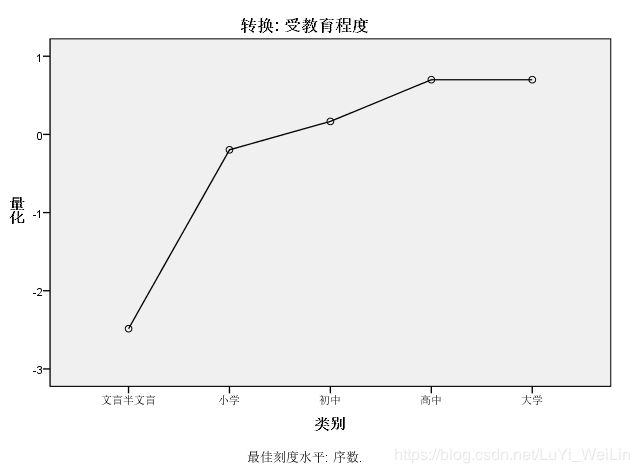
回到数据视图，可以看到，各变量经过最佳尺度变换，对分类或有序变量进行了数值量化后的数据列，各数据轨迹列由左往右，首列为因变量，其他列与自变量的顺序一致。
结合查看“转换图”，我们查看图知道文盲半文盲和小学间差了0.25，文化程度回归系数为-0.446，所以小学比文盲半文盲平均少生0.25*0.446约等于1个小孩
