拉格朗日乘子法和KKT条件

这里简单说一下拉格朗日乘子法的原理和insight.

等式约束

拉格朗日乘子法主要是用于解决有约束的优化问题. 比如最基本的等式约束
$$\begin{gathered} \max f(x,y) \\ s.t.,g(x,y)=0 \end{gathered}$$
我们想求$f(x,y)$的最大值,本身这个三维函数是定义在实平面上的, 他有自己的极值和最值. 但是加上了约束之后,我们就不能在整个实平面上找极值最值了, 我们得在$g(x,y)=0$这条线上找$f(x,y)$的最值.

一个observation是,如果我们令$f(x,y)=d$, 我们就能在平面上为不同的$d$值画出很多等高线, 这时我们再把$g(x,y)=0$也画上去可以得到下图(基本任何教程都会出现一张经典的图)

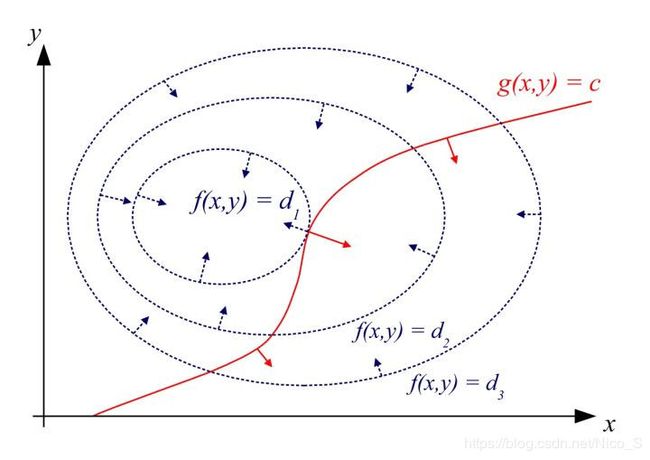
如果我们要从$g(x,y)=0$这条线上找极值, 比如说我们找到在点$(x_0,y_0)$处找到了极值$f(x_0,y_0)=d_1$. 这时可以看到, $g(x,y)=0$这条线是与$f(x,y)=d_1$这个等高线相切的, 这就意味着$g(x,y)=0$这条线在$(x_0,y_0)$处的切线方向与$f(x,y)=d_1$这个等高线在$(x_0,y_0)$处的切线方向共线(可能同向也可能反向), 即有:
$$\begin{gathered} {\frac{df(x,y)}{dx}|}_{(x_0,y_0)}=\lambda {\frac{dg(x,y)}{dx}|}_{(x_0,y_0)} \\ {\frac{df(x,y)}{dy}|}_{(x_0,y_0)}=\lambda {\frac{dg(x,y)}{dy}|}_{(x_0,y_0)} \end{gathered}$$

按照这个性质,我们不妨构造拉格朗日函数$\mathcal{L}(x,y,\lambda )=f(x,y)-\lambda g(x,y)$, 其中$\lambda$被称为拉格朗日乘子. 此时, $\mathcal{L}(x,y,\lambda )$的极值等于$f(x,y)$在$g(x,y)=0$限制下的极值, 原问题可转化为以下无约束优化问题
$$\max \mathcal{L}(x,y,\lambda )=f(x,y)-\lambda g(x,y),\lambda \in R$$

一个简单的验证方法是求解这个无约束问题, 为了找极值, 我们会令
$$\begin{gathered} \frac{d\mathcal{L}(x,y,\lambda )}{dx}=\frac{df(x,y)}{dx}-\lambda \frac{dg(x,y)}{dx}=0 \\ \frac{d\mathcal{L}(x,y,\lambda )}{dy}=\frac{df(x,y)}{dy}-\lambda \frac{dg(x,y)}{dy}=0 \\ \frac{d\mathcal{L}(x,y,\lambda )}{d\lambda }=g(x,y)=0 \end{gathered}$$

可以看到,其实求解这个新问题的过程就是在求解旧问题. 这三个方程中前两个其实就是$(x_0,y_0)$处切线共线, 最后一个就是原问题的约束.

Remark: 拉格朗日乘子法解出的是极值,并不是最值; 而且我们只知道他是极值,不知道是极大值还是极小值. 因此, 我们还需要带入一些具体的函数值才能确定哪个是最大值还是最小值.

不等式约束

不等式约束的一般情况如下. 遇到不同形式的问题, 我们可以通过加负号把问题转换为以下形式
$$\begin{gathered} \max f(x,y) \\ s.t.,g(x,y)\ge 0 \end{gathered}$$

不等式约束和等式约束有啥区别尼?区别在于现在$f(x,y)$的最值可能取在$g(x,y)=0$上, 也有可能取在$g(x,y)>0$内. 我们先来看在$g(x,y)=0$上的情况.

如果最值取在$g(x,y)=0$上, 我们直接可以把$g(x,y)\ge 0$变为$g(x,y)=0$, 这样问题就变成了等式约束问题:
$$\max \mathcal{L}(x,y,\lambda )=f(x,y)-\lambda g(x,y)$$

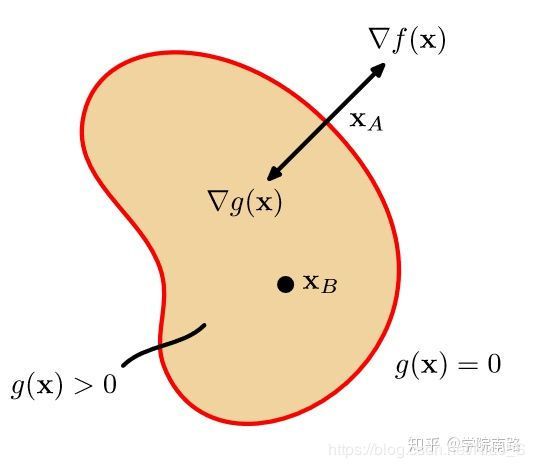
与之前不同的是, 此时我们对$\lambda$的取值有些限制. 如上图所示, 假设我们在$f(x_0,y_0)$取到最大值; 且$g(x,y)=0$内部是$g(x,y)>0$, 外部是$g(x,y)<0$, 因此$g(x,y)$在极值点的梯度方向是朝内的(梯度方向是函数值增加最快的方向). 反观$f(x,y)$, 由于$f(x_0,y_0)$是最大值点, 因此对于所有$g(x,y)>0$的区域 (曲线内), $f$的取值都不可能比$f(x_0,y_0)$大, 因此, 比$f(x_0,y_0)$大的值只可能在曲线外,因此梯度方向朝外.
综上,在最大值点,原函数的梯度方向和约束函数的梯度方向一定是相反的! 因此
$$\max \mathcal{L}(x,y,\lambda )=f(x,y)-\lambda g(x,y),\lambda \le 0$$
或
$$\max \mathcal{L}(x,y,\lambda )=f(x,y)+\lambda g(x,y),\lambda \ge 0$$

好,现在我们反过来看最大值取在$g(x,y)>0$内的情况, 此时, 其实$g(x,y)$ 对$f(x,y)$已经没有限制作用了,因为最大值的临域都是可以取到的.

为了融合两个情况,我们引入松弛互补条件（completeness and slackness condition) $\lambda g(x,y)=0$. 最终, 原问题转换为
$$\begin{gathered} \max \mathcal{L}(x,y,\lambda )=f(x,y)+\lambda g(x,y) \\ s.t.,g(x,y)\ge 0,\lambda \ge 0,\lambda g(x,y)=0 \end{gathered}$$
求解这个问题,我们需要
$$\begin{gathered} \frac{d\mathcal{L}(x,y,\lambda )}{dx}=\frac{df(x,y)}{dx}+\lambda \frac{dg(x,y)}{dx}=0 \\ \frac{d\mathcal{L}(x,y,\lambda )}{dy}=\frac{df(x,y)}{dy}+\lambda \frac{dg(x,y)}{dy}=0 \\ \lambda g(x,y)=0 \end{gathered}$$