2020暑假集训成果

原本觉得网上集训效果会很差,没想到也学到了不少知识,原本只想写一个题单的…有突然想到我这脑子笨,还是写一下具体的收获吧.

单调栈(笛卡尔树)

先粘一颗笛卡尔树…

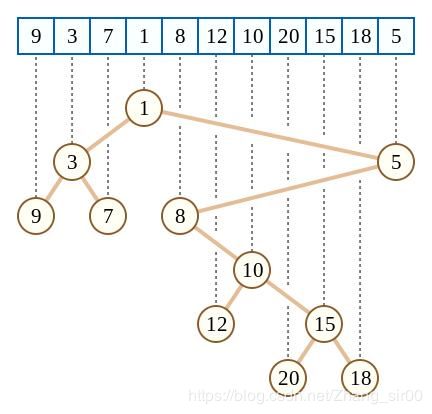简单观察就可以发现,根节点对应的值比子节点小(像堆),根节点的下标值比左儿子大,比右儿子小(像二叉检索树)

所以不难发现,根节点的自述大小(含自身)就是以当前值为最值的管辖范围(从左树的任意一个节点开始到右树的任意一个节点结束,根节点一定是最值)这里我们不构建笛卡尔树,而是通过运用单调栈就可以实现O(n)的查询所有节点的子树范围(也就是所谓的最大管辖区间)
下面是代码(简单的没话说):

#include 
#include 
#define MAX 1000
#define inf 0x3f3f3f3f
using namespace std;
int k[MAX];
int a[MAX];
stack<pair<int,int> > st;//id&pos 
pair<int,int> ans[MAX];//l&r
int main()
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	for(int i=1;i<=n;i++)
	k[i]=a[i];
	k[n+1]=inf;
	for(int i=1;i<=n+1;i++)
	{
		pair<int,int> t;
		if(st.empty()||k[st.top().second]>k[i])
		{
			st.push({i,i});
		}
		else
		{
			while(!st.empty()&&k[st.top().second]<k[i])
			{
				t=st.top();
				ans[t.first]={t.second,i-1};
				st.pop();
			}
			k[t.second]=k[i];
			st.push({i,t.second});
		}
		
	}
	for(int i=1;i<=n;i++)
		printf("%d:%d->%d\n",a[i],ans[i].first,ans[i].second);
	return 0;
}
/*
10
1 5 4 3 2 10 6 7 9 8
*/

有了这个范围,我们就可以很方便的求出节点的贡献或者节点的最优方案等等(所以它只可能是一个综合题的一小部分…)

单调队列(滑动窗口)

队友说可以实现单调栈一样的功能(没有理解…)
目前只理解到可以O(n)的求解滑动窗口问题(然而nlogn的树状数组也能解)
滑动窗口
题解(很详细)

图论建图思想(以矛盾建边)

建图–图论无穷魅力的源泉,通过神奇的转换,一个和图半毛钱搭不上关系的题,也可以通过图论解.以矛盾建边无疑是其中的一个转换思想(常用于二分图),如果A和B不能共存就在A和B之间建一条边,总点数-最大匹配,就是,不产生矛盾的最大集合(最大独立集)
这已经不是第一次遇到这种思想了…
题目链接

分治(笛卡尔树)

连着两场出了两道思路基本相同的题,不学对不起出题人(QWQ)
其实这种分治的DFS路线就是笛卡尔树的深度优先遍历所以也没什么好说的,处理的好完全可以用单调栈代替.
题目链接

bitset(一个简单的STL,方便进行位运算)

这个实在是没什么好说的…和正常的STL基本没什么区别

分层图(最短路加强版)

这种题给的很明显–>在最短路的基础上给你K次机会吧边权变为0,问你最小花费,就是把原本的一层图改为K层,上面的层次向下面的层次添加代价为0的边来表示将这条路的花费变为零,但是这样处理的效率稍稍低一点,我们可以采用类似DP的方式,开一个 dis[i][j] 来表示到达i节点用掉j条免费边的最小花费,不断向下推就完事(粗暴到代码看起来就像是暴力)

题目链接