电荷与电势能也和人脸识别有关?——UniformFace论文阅读
电荷与电势能也和人脸识别有关?——UniformFace论文阅读
电荷与电势能也能跟人脸识别有关吗???对!!UniformFace的作者就在它们之间建立了联系。今天,我来和大家一起分享一下这篇论文(UniformFace: Learning Deep Equidistributed Representation for Face Recognition )吧。
Introduction
一般来说,一个实际的人脸识别系统有四个主要步骤:人脸检测、人脸对齐、人脸表示和人脸匹配。在其中,人脸表示(Face Representation)是从不同的人身上提取人脸识别特征的关键。近年来,随着深度学习的快速发展,基于卷积神经网络(CNNs)的人脸表示技术得到了长足的发展。而决定CNN特征识别能力的关键因素有三个,分别是:训练数据、网络结构和损失函数。在这篇文章中,作者主要关注的是第三个方面,也就是如何设计一个更有效的损失函数。
既然讲到损失,我们最常见、最了解的便是多分类问题使用到的Softmax Loss了。Softmax Loss广泛应用于训练CNN特征,它通常被定义为最后一个完全连接层、Softmax函数和交叉熵损失的组合,其表示如下:
L s = − 1 N ∑ i = 1 N l o g e W y i T x i + b y i ∑ j = 1 M e W j T x i + b j L_s = -\frac1N \sum_{i=1}^{N}log\frac{e^{\boldsymbol{W}^{T}_{y_i}\boldsymbol{x}_i + b_{y_i}}}{\sum_{j=1}^M e^{\boldsymbol{W}^{T}_{j}\boldsymbol{x}_i + b_{j}}} Ls=−N1i=1∑Nlog∑j=1MeWjTxi+bjeWyiTxi+byi
而Softmax Loss学习到的特征具有内在的角度分布,这表明余弦距离是度量,因此损失函数又可以写为如下的这种形式:
L m = − 1 N ∑ i = 1 N l o g e ∣ ∣ x i ∣ ∣ c o s ( θ y i , i ) ∑ j = 1 M e ∣ ∣ x i ∣ ∣ c o s ( θ j , i ) L_m = -\frac1N \sum_{i = 1}^Nlog \frac{e^{||\boldsymbol{x}_i||cos(\theta_{y_i,i})}}{\sum_{j=1}^M e^{||\boldsymbol{x}_i||cos(\theta_{j,i})}} Lm=−N1i=1∑Nlog∑j=1Me∣∣xi∣∣cos(θj,i)e∣∣xi∣∣cos(θyi,i)
Sphereface的作者在此基础上进一步改进,在sample point和target class之间的角度乘以了margin参数m,通过A-Softmax损失操纵决策边界以产生角度裕度:
L a − s = − 1 N ∑ i = 1 N l o g e ∣ ∣ x i ∣ ∣ ψ ( θ y i , i ) e ∣ ∣ x i ∣ ∣ ψ ( θ y i , i ) + ∑ j ≠ y i e ∣ ∣ x i ∣ ∣ c o s ( θ j , i ) L_{a-s} = -\frac1N \sum_{i=1}^Nlog \frac{e^{||\boldsymbol{x}_i||\psi(\theta_{y_i,i})}}{e^{||\boldsymbol{x}_i||\psi(\theta_{y_i,i})}+ \sum_{j \neq y_i} e^{||\boldsymbol{x}_i||cos(\theta_{j,i})}} La−s=−N1i=1∑Nloge∣∣xi∣∣ψ(θyi,i)+∑j=yie∣∣xi∣∣cos(θj,i)e∣∣xi∣∣ψ(θyi,i)
其中
ψ ( θ y i , i ) = ( − 1 ) k c o s ( m θ y i , i ) − 2 k , θ y i , i ∈ [ k π m , ( k + 1 ) π m ] , k ∈ [ 0 , m − 1 ] \psi(\theta_{y_i,i}) = (-1)^kcos(m\theta_{y_i,i}) - 2k,\\ \theta_{y_i,i} \in [\frac{k\pi}{m}, \frac{(k+1)\pi}{m}],\\ k \in [0,m-1] ψ(θyi,i)=(−1)kcos(mθyi,i)−2k,θyi,i∈[mkπ,m(k+1)π],k∈[0,m−1]
从图中我们可以看到,与前两者相比,A-Softmax在类别的角度维度上的分类更加分明,决策边界明显扩大。同时,从图中我们也可以看出上文中提到的Softmax内在的角度分布特性。
Motivation
然而,Sphereface还是存在一定的缺陷。我们在模式识别问题中往往希望最终实现类内距离小,而类间距离大。Sphereface通过A-softmax将同一类的特征约束到了较小的区域,使得类内距离小。但是,它却没有考虑特征在整体超球流形中的分布,也就是类间距离。如下图所示,0、1两个类别间的距离相对较小,也就是特征分布的最小类间距离较小。

从上面的推演中我们可以想到,最小类间距离可以衡量我们的特征分布到底好不好,最小类间距越大,我们的特征分布应该会更好。那么,我们自然可以联想到:当特征分布均匀时,我们将拥有最大的最小类间距,就像图中所示,显然,这个均匀分布的最小类间距要大于刚刚的Sphereface。因此,作者的目标是能够实现这样的分布,以期在人脸识别问题上取得更好的效果。

Solution
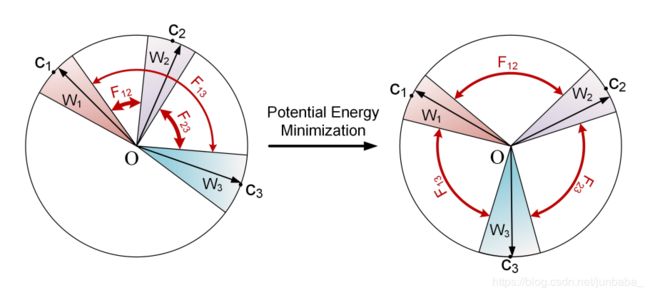
那么,我们该如何设置损失函数来使得特征分布更加均匀呢?作者这里联想到了电势能——由于不同类的面应该分开,我们认为类中心就像等量的电荷,每个中心排斥其他中心;同时,球体表面的电荷在均匀分布时的势能最小。如图所示,我们可以看做是以电势能为损失函数,通过优化使损失函数达到最小值时,电荷会均匀分布。那么,将电荷替换为类中心时,我们用类似电势能的公式作为损失函数,最终类中心应该能够均匀分布。
作者受到此启发,也类比了电场力、电势能的公式。其中, c j 1 , c j 2 c_{j_1},c_{j_2} cj1,cj2表示两个类中心。首先,力与距离的平方成反比:
F = λ 1 d ( c j 1 , c j 2 ) 2 F = \lambda \frac{1}{d(\boldsymbol{c}_{j_1},\boldsymbol{c}_{j_2})^2} F=λd(cj1,cj2)21
对力进行距离上的积分,我们得到了能量:
E = ∫ d ( c j 1 , c j 2 ) ∞ λ 1 x 2 d x = λ 1 d ( c j 1 , c j 2 ) E = \int_{d(\boldsymbol{c}_{j_1},\boldsymbol{c}_{j_2})}^{\infty} \lambda \frac{1}{x^2}dx = \lambda \frac{1}{d(\boldsymbol{c}_{j_1},\boldsymbol{c}_{j_2})} E=∫d(cj1,cj2)∞λx21dx=λd(cj1,cj2)1
类比能量,作者写出了Loss函数,命名为Uniform Loss:
L u = λ M ( M − 1 ) ∑ j 1 = 1 M ∑ j 1 ≠ j 2 1 d ( c j 1 , c j 2 ) L_u = \frac{\lambda}{M(M-1)}\sum_{j_1=1}^M \sum_{j_1 \neq j_2}\frac{1}{d(\boldsymbol{c}_{j_1},\boldsymbol{c}_{j_2})} Lu=M(M−1)λj1=1∑Mj1=j2∑d(cj1,cj2)1
由于类中心 c j c_j cj在训练过程中不断变化,在每次迭代中我们都要利用整个训练集更新 c j c_j cj,耗时过长,在实际中是不适用的。因此,作者采用了一种改进的方法,在每个mini-batch上更新类中心。
Δ c j = ∑ i = 1 n δ ( y i = j ) ⋅ ( c j − x i ) 1 + ∑ i = 1 n δ ( y i = j ) \Delta \boldsymbol{c}_j = \frac{\sum_{i=1}^{n} \delta(y_i = j)\cdot (\boldsymbol{c}_j-\boldsymbol{x}_i)}{1 + \sum_{i=1}^{n}\delta(y_i = j)} Δcj=1+∑i=1nδ(yi=j)∑i=1nδ(yi=j)⋅(cj−xi)
最终总体Loss函数设计为A-Softmax Loss和Uniform Loss的结合:
L = L a − s + L u L = L_{a-s} + L_u L=La−s+Lu
Experiments
接下来我们来讲作者在上述基础上进行的实验。
数据集
MegaFace: Megaface数据集是由华盛顿大学提供的一个大规模人脸属性数据集,共包含了690000个人的上百万张人脸图片,能够评估人脸识别算法在百万级的性能。

IJB-A: IJB-A是一个用于人脸检测和识别的数据库,包含24327个图像和49759个人脸。

YTF: YTF数据集包含了从YouTube上下载的1595个不同人物的3425个视频,这些人的姿势、光照和表情都有不同的变化,是一个用于无约束人脸识别的流行数据集。
LFW: LFW是一个著名的用于人脸识别的网络采集图像集,它包含来自5749个不同身份的13233个图像。
实现细节
具体实现UniformFace时,作者使用了ResNet作为CNN的架构。
残差单元:
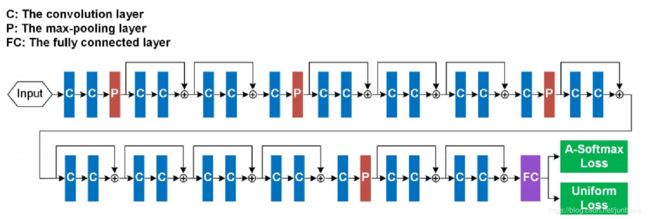
最终网络结构,可以看到,其使用了多个残差单元,并且最终的损失是Uniform Loss与A-Softmax Loss相加:
实验结果
在Megaface数据集上的实验情况:
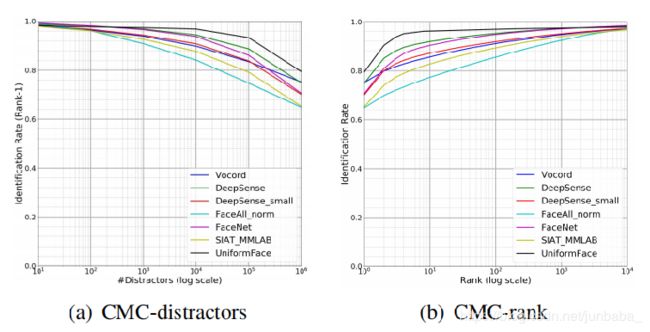
首先是CMC和ROC曲线,可以看到,黑色的UniformFace要优于其它的几种方法。
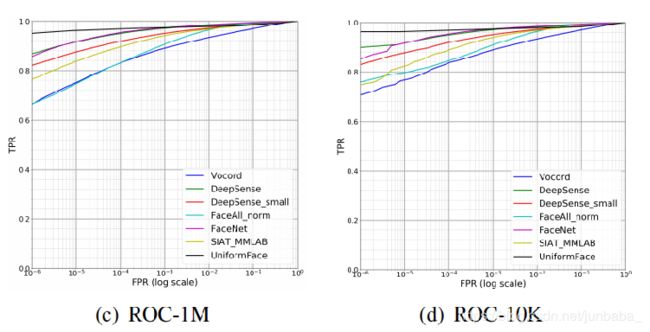
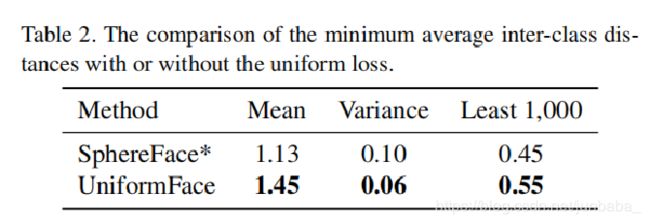
另外,与SphereFace相比,UniformFace的最小平均类间距离更大,方差更小,可见其特征分布更好。
在SphereFace、ArcFace等方法中添加了Uniform Loss后,检测的Rank-1准确率都有所提升。
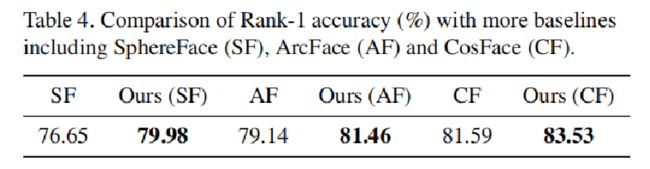
在IJB-A数据集上的实验情况:
可以看到,UniformFace与PAM、3DMM、DR-GAN和PRN等新近提出的、利用了较强的姿态先验信息的方法相比取得了比较有竞争力的结果。
在YTF数据集和LFW数据集上的实验情况:
我们可以看到,UniformFace相比其他方法,在使用更少的训练数据、更简洁的模型的情况下,取得了较为理想的结果。
另外,作者在这里还与单独使用A-Softmax Loss进行了对比。单独使用A-Softmax Loss时,随着margin参数m的增大,每个类间的平均间隔增大,特征分布更加均匀,但是带来了学习上的困难。而UniformFace有效改变了这点。
作者认为,导致上述实验结果的主要原因是是Uniform Loss导致了均匀分布表示,充分利用了整体特征空间。
Future
本文中作者为每个类中心设置相同的电荷量,类间排斥只与距离有关。为了获得更具细粒度的表示,作者认为,在未来可以学习不同类的数据相关电荷量。