PyTorch学习笔记(三)参数初始化与各种Norm层
Environment
- OS: macOS Mojave
- Python version: 3.7
- PyTorch version: 1.4.0
- IDE: PyCharm
文章目录
- 0. 写在前面
- 1. 初始化
- 1.1 Xavier 初始化
- 1.1.1 Xavier 均匀分布
- 1.1.2 Xavier 正态分布
- 1.1.3 计算增益值 gain
- 1.2 kaiming 初始化
- 1.2.1 kaiming 正态分布
- 1.2.2 kaiming 均匀分布
- 1.3 均匀分布初始化
- 1.4 正态分布初始化
- 1.5 常数初始化
- 1.6 正交初始化
- 1.7 单位矩阵初始化
- 1.8 稀疏矩阵初始化
- 2. Norm 层
- 2.1 Batch Normalization
- 2.1.1 running_mean 和 running_var 属性
- 2.1.2 weight 和 bias 属性
- 手动计算
- 2.2 Layer Normalization
- 2.2.1 weight 和 bias 属性
- 手动计算
- 2.3 Instance Normalization
- 2.3.1 running_mean 和 running_var 属性
- 手动计算
- 2.4 Group Normalization
- 2.4.1 weight 和 bias 属性
- 手动计算
0. 写在前面
数据在神经网络模型的层与层之间传播,数据过大或或小都会使训练遇上麻烦。合理的参数初始化和 Normalization 能够使模型中数据分布合理,让训练能够顺利地进行。
1. 初始化
PyTorch 中的 torch.nn.init 模块提供了十种初始化的方式,这里简单记录一下。
为改善梯度消失和爆炸的问题,需要保证神经网络中数据分布在合适的范围,这就是方差一致性。经典的 Xavier 和 kaiming 初始化都是从这个原则得来。
对于两个独立随机变量,它们乘积的方差为
D ( X Y ) = 方 差 的 定 义 E [ ( X Y − E ( X Y ) ) 2 ] = E [ X 2 Y 2 − 2 X Y E ( X Y ) + E 2 ( X Y ) ] = 期 望 的 线 性 性 质 E ( X 2 Y 2 ) − 2 E 2 ( X Y ) + E 2 ( X Y ) = E ( X 2 Y 2 ) − E 2 ( X Y ) D(XY) \overset{方差的定义}= E[(XY - E(XY))^2] \\ \ \\ = E[X^2 Y^2 - 2XY E(XY) + E^2(XY)] \\ \ \\ \overset{期望的线性性质}= E(X^2 Y^2) - 2E^2(XY) + E^2(XY) = E(X^2 Y^2) - E^2(XY) D(XY)=方差的定义E[(XY−E(XY))2] =E[X2Y2−2XYE(XY)+E2(XY)] =期望的线性性质E(X2Y2)−2E2(XY)+E2(XY)=E(X2Y2)−E2(XY)
因为,当 X, Y 相互独立时
E ( X Y ) = E ( X ) E ( Y ) , E ( X 2 Y 2 ) = E ( X 2 ) E ( Y 2 ) E(XY) = E(X) E(Y), E(X^2 Y^2) = E(X^2) E(Y^2) E(XY)=E(X)E(Y),E(X2Y2)=E(X2)E(Y2)
所以,
D ( X Y ) = E ( X 2 ) E ( Y 2 ) − [ E ( X ) E ( Y ) ] 2 D(XY) = E(X^2) E(Y^2) - [E(X)E(Y)]^2 D(XY)=E(X2)E(Y2)−[E(X)E(Y)]2
又因
E ( X 2 ) = D ( X ) + E 2 ( X ) , E ( Y 2 ) = D ( Y ) + E 2 ( Y ) E(X^2) = D(X) + E^2(X), E(Y^2) = D(Y) + E^2(Y) E(X2)=D(X)+E2(X),E(Y2)=D(Y)+E2(Y)
进一步转化
D ( X Y ) = [ D ( X ) + E 2 ( X ) ] [ D ( Y ) + E 2 ( Y ) ] − [ E ( X ) E ( Y ) ] 2 = D ( X ) D ( Y ) + D ( X ) E 2 ( Y ) + D ( Y ) E 2 ( X ) D(XY) = [D(X) + E^2(X)][D(Y) + E^2(Y)] - [E(X)E(Y)]^2 \\ \ \\ = D(X)D(Y) + D(X)E^2(Y) + D(Y)E^2(X) D(XY)=[D(X)+E2(X)][D(Y)+E2(Y)]−[E(X)E(Y)]2 =D(X)D(Y)+D(X)E2(Y)+D(Y)E2(X)
当 E ( X ) = E ( Y ) = 0 E(X) = E(Y) = 0 E(X)=E(Y)=0 时,
D ( X Y ) = D ( X ) D ( Y ) D(XY) = D(X)D(Y) D(XY)=D(X)D(Y)
由此可知,当神经网络第 l − 1 l - 1 l−1 层中的数据方差为 V a r [ l − 1 ] Var^{[l-1]} Var[l−1] ,那么在含有 n n n 个神经元的第 l l l 层,且权重的方差为 1 1 1 时,该层数据的方差理论上将是
V a r [ l ] = V a r [ i − 1 ] × n × 1 = n V a r [ l − 1 ] Var^{[l]} = Var^{[i-1]} \times n \times 1 = n Var^{[l-1]} Var[l]=Var[i−1]×n×1=nVar[l−1]
1.1 Xavier 初始化
Xavier 初始化主要针对饱和激活函数,如 Sigmoid、Tanh。具体理论参考文献 Understanding the difficulty of training deep feedforward neural networks
1.1.1 Xavier 均匀分布
为了保证每一层中数据的方差为 1 1 1 ,即 n [ l − 1 ] × D ( W [ l ] ) = n [ l ] × D ( W [ l ] ) = 1 n^{[l-1]} \times D(W^{[l]}) = n^{[l]} \times D(W^{[l]}) = 1 n[l−1]×D(W[l])=n[l]×D(W[l])=1 ,
折衷地,有 D ( W [ l ] ) = 2 n [ l − 1 ] + n [ l ] D(W^{[l]}) = \frac{2}{n^{[l-1]} + n^{[l]}} D(W[l])=n[l−1]+n[l]2 ,
对于均匀分布的 W W W , W ∼ U [ − a , a ] W \sim U[-a, a] W∼U[−a,a] ,方差 D ( W ) = ( 2 a ) 2 12 = a 2 3 D(W) = \frac{(2a)^2}{12} = \frac{a^2}{3} D(W)=12(2a)2=3a2 ,
根据上面两式,设置均匀分布中的参数 a = 6 n [ l − 1 ] + n l a = \sqrt{\frac{6}{n^{[l-1]} + n^l}} a=n[l−1]+nl6
另外,考虑到激活函数的存在,设置增益 gain,得 a = gain 6 n [ l − 1 ] + n l a = \text{gain} \sqrt{\frac{6}{n^{[l-1]} + n^l}} a=gainn[l−1]+nl6
torch.nn.init.xavier_uniform_ 实现 Xavier 均匀分布初始化
import torch
from torch.nn import Module, Conv2d, Linear
class Net(Module):
def __init__(self):
super(Net, self).__init__()
pass # 定义网络层
self._init_params() # 执行初始化
def forward(self, x):
pass # 定义前向传播
def _init_params(self):
for m in self.modules():
if isinstance(m, (Conv2d, Linear)): # 对卷积层和线性层的权重执行 Xavier 均匀分布初始化
torch.nn.init.xavier_uniform_(
tensor=m.weight.data, # 传入需要初始化的对象
gain=torch.nn.init.calculate_gain('tanh') # 增益,因激活函数而异的一个缩放因子
)
"""
# 手动设定 Xavier 均匀分布初始化
a = np.sqrt(6 / (m.in_features + m.out_features))
gain = torch.nn.init.calculate_gain('tanh')
a *= gain
torch.nn.init.uniform_(m.weight.data, -a, a)
"""
torch.nn.init.constant_(m.bias.data, 0)
if __name__ == '__main__':
net = Net()
1.1.2 Xavier 正态分布
均值为零,标准差为 gain ∗ 2 n [ l − 1 ] + n l \text{gain} * \sqrt{\frac{2}{n^{[l-1]} + n^l}} gain∗n[l−1]+nl2
torch.nn.init.xavier.normal 实现 Xavier 正态分布初始化,使用同 Xavier 均匀分布函数。
1.1.3 计算增益值 gain
计算数据的方差在神经网络层间关系时,未考虑到激活函数的存在,因为激活函数会造成数据分布的改变,因此在初始化参数时,需要计算增益值 gain
torch.nn.init.calculate_gain(nonlinearity, param=None)
| nonlinearity | gain |
|---|---|
| Linear / Identity | 1 1 1 |
| Conv{1,2,3}d | 1 1 1 |
| Sigmoid | 1 1 1 |
| Tanh | 5 3 \frac{5}{3} 35 |
| ReLU | 2 \sqrt{2} 2 |
| Leaky Relu | 2 1 + negative_slope 2 \sqrt{\frac{2}{1 + \text{negative\_slope}^2}} 1+negative_slope22 |
1.2 kaiming 初始化
当 Xavier 初始化遇到非饱和激活函数(如 ReLu、LeakyReLU 等)时,效果并不太好。因此主要针对非饱和激活函数的 kaiming 初始化被提出。具体理论参考文献 Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification
1.2.1 kaiming 正态分布
均值为零,标准差为 2 ( 1 + a 2 ) × n [ l ] \sqrt{\frac{2}{(1 + a^2) \times n^{[l]}}} (1+a2)×n[l]2,其中 a a a 为激活函数负半轴的斜率。
torch.nn.init.xavier_normal_ 实现 kaiming 正态分布初始化
import torch
from torch.nn import Module, Conv2d, Linear
class Net(Module):
def __init__(self):
super(Net, self).__init__()
pass # 定义网络层
self._init_params() # 执行初始化
def forward(self, x):
pass # 定义前向传播
def _init_params(self):
for m in self.modules():
if isinstance(m, (Conv2d, Linear)): # 对卷积层和线性层的权重执行 Xavier 均匀分布初始化
torch.nn.init.kaiming_normal_(
tensor=m.weight.data, # 需要初始化的对象
a=0, # LeakyReLU 负半轴斜率,默认为 0,即 ReLU
mode='fan_out', # 可传入 'fan_in' 或 'fan_out'两种值,默认为 'fan_in'
# 'fan_in' 表示设置标准差时,分母为输入层的神经元个数,正向传播时方差一致
# 'fan_out' 表示设置标准差时,分母为该层神经元个数,反向传播时方差一致
nonlinearity='leaky_relu' # 网络中使用的激活函数,默认为 'leaky_relu'
)
"""
# 手动设定 kaiming 正态分布初始化
a = 0
torch.nn.init.normal_(m.weight.data, std=np.sqrt(2 / (1 + a**2) * m.out_features))
"""
torch.nn.init.constant_(m.bias.data, 0)
if __name__ == '__main__':
net = Net()
1.2.2 kaiming 均匀分布
均匀分布的上下限为 6 ( 1 + a 2 ) × n [ l ] \sqrt{\frac{6}{(1+a^2) \times n^{[l]}}} (1+a2)×n[l]6
torch.nn.init.xavier_uniform_ 实现 kaiming 均匀分布初始化,使用方式同 kaiming 正态分布。
1.3 均匀分布初始化
torch.nn.init.uniform_
import torch
from torch.nn import Conv2d
import matplotlib.pyplot as plt
import seaborn as sns
conv = Conv2d(in_channels=64, out_channels=256, kernel_size=3)
torch.nn.init.uniform_(conv.weight.data, a=0.0, b=1.0) # a, b 为均匀分布的上下限
sns.set_style('whitegrid')
plt.hist(conv.weight.data.detach().numpy().ravel())
plt.show()
1.4 正态分布初始化
torch.nn.init.normal_
import torch
from torch.nn import Conv2d
import matplotlib.pyplot as plt
import seaborn as sns
conv = Conv2d(in_channels=64, out_channels=256, kernel_size=3)
torch.nn.init.normal_(conv.weight.data, mean=0.0, std=1.0)
sns.set_style('whitegrid')
plt.hist(conv.weight.data.detach().numpy().ravel(), bins=20)
plt.show()
1.5 常数初始化
torch.nn.init.constant_ 实现常数初始化
import torch
w = torch.empty(8, 2)
torch.nn.init.constant_(w, val=0)
1.6 正交初始化
torch.nn.init.orthogonal_ 使得 tensor 正交
import torch
from torch.nn import Conv2d
torch.manual_seed(0)
conv = Conv2d(in_channels=3, out_channels=64, kernel_size=7)
torch.nn.init.orthogonal_(conv.weight.data, gain=1.0)
w = conv.weight.data[0, 0]
# 7 x 7 并不太多,所以乘积并不为零
print(w[:, 0] @ w[:, 1]) # tensor(0.0596)
print(w[:, 0] @ w[:, 2]) # tensor(0.0124)
print(w[:, 1] @ w[:, 2]) # tensor(0.0103)
1.7 单位矩阵初始化
torch.nn.init.eye_ 实现单位矩阵初始化,仅支持传入二维或三维张量,如全连接层的权重
import torch
from torch.nn import Linear
linear = Linear(in_features=2048, out_features=1000)
torch.nn.init.eye_(linear.weight.data)
print(linear.weight.data)
# tensor([[1., 0., 0., ..., 0., 0., 0.],
# [0., 1., 0., ..., 0., 0., 0.],
# [0., 0., 1., ..., 0., 0., 0.],
# ...,
# [0., 0., 0., ..., 0., 0., 0.],
# [0., 0., 0., ..., 0., 0., 0.],
# [0., 0., 0., ..., 0., 0., 0.]])
1.8 稀疏矩阵初始化
torch.nn.init.orthogonal_ 使得矩阵每一列有一部分为零,其余非零元素服从以零为期望的正态分布。仅支持传入二维或三维张量,如全连接层的权重。参考文献 Deep learning via Hessian-free optimization。
import torch
from torch.nn import Linear
import matplotlib.pyplot as plt
import seaborn as sns
torch.manual_seed(0)
linear = Linear(in_features=64, out_features=256)
# sparsity 传入每一列零元素的比例,std 传入非零元素正态分布的标准差
torch.nn.init.sparse_(linear.weight.data, sparsity=0.1, std=0.01)
sns.set_style('whitegrid')
plt.hist(linear.weight.data.detach().numpy().ravel(), bins=20)
plt.show()
2. Norm 层
PyTorch 提供了四种常用的 Norm 层,包括 BatchNorm、LayerNorm、InstanceNorm 和 GroupNorm。BatchNorm 和 InstanceNorm 的基类为 torch.nn._NormBase,该类继承于 torch.nn.Module;LayerNorm 和 GroupNorm 直接继承于 torch.nn.Module。
创建一个小数据集为例,观察对于 2d 的 Norm 层的效果
import torch
feature_maps_1 = torch.tensor([
[
[0., 2],
[4, 6]
],
[
[2, 4],
[6, 8],
],
[
[4, 6],
[8, 10]
],
[
[6, 8],
[10, 12]
]
])
feature_maps_2 = torch.tensor([
[
[1., 3],
[5, 7]
],
[
[3, 5],
[7, 9],
],
[
[5, 7],
[9, 11]
],
[
[7, 9],
[11, 13]
]
])
feature_maps_batch = torch.stack((feature_maps_1, feature_maps_2), dim=0)
print('input data shape:', feature_maps_batch.size())
# input data shape: torch.Size([2, 4, 2, 2])
2.1 Batch Normalization
对隐藏层的 Normalization 操作使得参数初始化变得不用那么讲究,训练更稳定。
from torch.nn import BatchNorm2d
bn = BatchNorm2d(
num_features=feature_maps_batch.size(1), # 样本的特征数
eps=1e-5, # 分母修正项
momentum=MOMENTUM, # 指数加权平均估计当前 mean/var
affine=True, # 是否需要 affine transform
track_running_stats=True # 追踪模型是 train 状态还是 eval 状态
)
# 打印初始的 running_mean 和 running_var
print(bn.running_mean, bn.running_var)
# tensor([0., 0., 0., 0.]) tensor([1., 1., 1., 1.])
# prop forward
output = bn(feature_maps_batch)
理解track_running_stats 参数,参考知乎 BatchNorm2d增加的参数track_running_stats如何理解?
2.1.1 running_mean 和 running_var 属性
加权均值,计算公式为
running_mean = ( 1 − momentum ) × pre_running_mean + momentum × mean_t \text{running\_mean} = (1 - \text{momentum}) \times \text{pre\_running\_mean} + \text{momentum} \times \text{mean\_t} running_mean=(1−momentum)×pre_running_mean+momentum×mean_t
加权方差,计算公式为
running_var = ( 1 − momentum ) × pre_running_var + momentum × var_t \text{running\_var} = (1 - \text{momentum}) \times \text{pre\_running\_var} + \text{momentum} \times \text{var\_t} running_var=(1−momentum)×pre_running_var+momentum×var_t
经过一波前向之后,
# 对于 BatchNorm2d 而言,
# running_mean 和 running_var 是一维的,长度与 num_features 相同
print(bn.running_mean.size()) # torch.Size([4])
print(bn.running_var.size()) # torch.Size([4])
print('running mean:', bn.running_mean)
# tensor([1.0500, 1.6500, 2.2500, 2.8500])
print('running var:', bn.running_var)
# tensor([2.5000, 2.5000, 2.5000, 2.5000])
2.1.2 weight 和 bias 属性
weight 为 affine transform 中的 gamma,bias 为 beta。
print(bn.weight.size()) # torch.Size([4])
print(bn.bias.size()) # torch.Size([4])
print(bn.weight)
# tensor([1., 1., 1., 1.], requires_grad=True)
print(bn.bias)
# tensor([0., 0., 0., 0.], requires_grad=True)
手动计算
对于 batch 中第一个 feature_map,手动实现 BatchNorm2d。需要注意,torch.var(unbiased=True) 中默认使用了方差的 Bessel’s correction,即计算样本方差而不是总体方差
first_map_in_batch = feature_maps_batch[:, 0, :, :]
# 在训练相中,进行 Normalization 时,使用的标准差为总体标准差,未经 Bessel's correction
out = (first_map_in_batch-first_map_in_batch.mean()) / first_map_in_batch.std(unbiased=False)
print('Output:\n', out)
# Output:
# tensor([[[-1.5275, -0.6547],
# [ 0.2182, 1.0911]],
# [[-1.0911, -0.2182],
# [ 0.6547, 1.5275]]])
# 计算 running_mean 和 running_var
running_mean, running_var = 0., 1.
print('running mean:',
(1 - MOMENTUM) * running_mean + MOMENTUM * first_map_in_batch.mean())
# running mean: tensor(1.0500)
print('running var:',
(1 - MOMENTUM) * running_var + MOMENTUM * first_map_in_batch.var())
# running var: tensor(2.5000)
2.2 Layer Normalization
Batch Normalization 不适用于变长的网络,如 RNN。对于这种网络,需要逐层计算均值和方差,进行 Normalization。
Layer Normalization 没有 running_mean 和 running_var,每一个元素有一个 weight 和 bias。
ln = LayerNorm(
normalized_shape=feature_maps_batch.size()[1:], # 该层特征形状
eps=1e-05,
elementwise_affine=True # 是否需要 affine transform
)
output = ln(feature_maps_batch)
2.2.1 weight 和 bias 属性
print(ln.weight.size()) # torch.Size([4, 2, 2])
print(=ln.bias.size()) # torch.Size([4, 2, 2])
手动计算
feature_map_layer_1 = feature_maps_batch[0]
out = (feature_map_layer_1 - feature_map_layer_1.mean()) / feature_map_layer_1.std(unbiased=False)
print(out)
# tensor([[[-1.8974, -1.2649],
# [-0.6325, 0.0000]],
#
# [[-1.2649, -0.6325],
# [ 0.0000, 0.6325]],
#
# [[-0.6325, 0.0000],
# [ 0.6325, 1.2649]],
#
# [[ 0.0000, 0.6325],
# [ 1.2649, 1.8974]]])
2.3 Instance Normalization
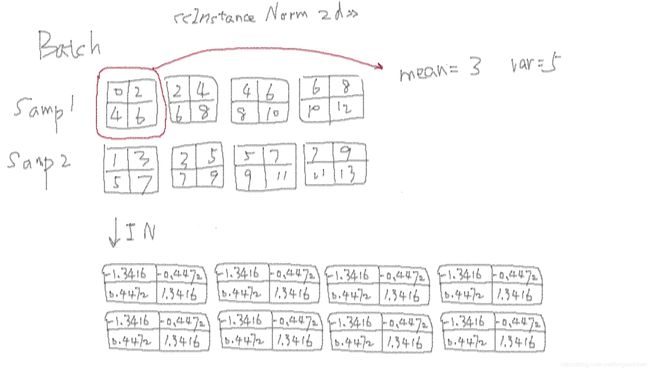
Batch Normalization 不适用于图像生成的任务(如GAN、Nueral Style Transfer),因此提出了 Instance Normalization,对逐个样本实例的逐个特征图计算均值和方差,进行 normalization。
torch.nn.InstanceNorm2d 的计算示意图
from torch.nn import InstanceNorm2d
instance_norm = InstanceNorm2d(
num_features=feature_maps_batch.size(1), # 一个样本的特征数,也就是卷积层的 out_channels
eps=1e-5, # 分母修正项
momentum=MOMENTUM, # 指数加权平均估计当前 mean / var
affine=True, # 是否需要 affine transform
track_running_stats=True # 追踪模型是 train 状态还是 eval 状态
)
# 打印初始的 running_mean 和 running_var
print(instance_norm.running_mean, instance_norm.running_var)
tensor([0., 0., 0., 0.]) tensor([1., 1., 1., 1.])
# forward
output = instance_norm(feature_maps_batch)
2.3.1 running_mean 和 running_var 属性
print('running mean shape:', instance_norm.running_mean.size())
# running mean shape: torch.Size([4])
print('running mean:', instance_norm.running_mean)
# running mean: tensor([1.7850, 2.8050, 3.8250, 4.8450])
print('running var shape:', instance_norm.running_var.size())
# running var shape: torch.Size([4])
print('running var:', instance_norm.running_var)
# running var: tensor([3.8900, 3.8900, 3.8900, 3.8900])
手动计算
对于 batch 中第一个样本的第一个 feature_map
instance = feature_maps_batch[0, 0, :, :]
out = (instance - instance.mean()) / instance.std(unbiased=False)
print(out)
# tensor([[-1.3416, -0.4472],
# [ 0.4472, 1.3416]])
2.4 Group Normalization
一般 batch size 为 64、128 或 256。当模型较大,而设置相对小的 batch size时,Batch Normalization 估计的均值和方差可能不准。Group Normalization 采用通道数来补偿较小的 batch,得到更好的均值和方差。
事实上,
- LayerNorm 就是
num_groups=1时的 GroupNorm - InstanceNorm 就是
num_groups=num_features时的 GroupNorm
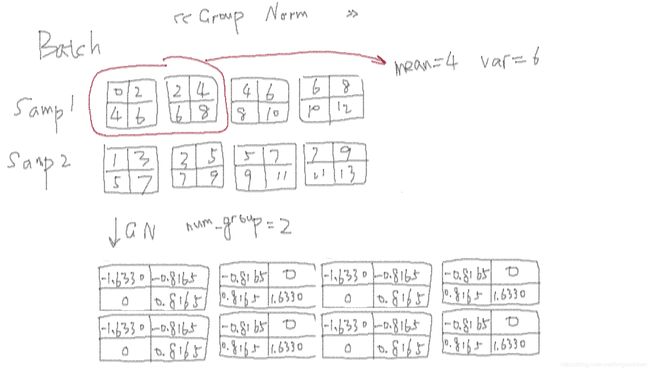
num_groups=2 时, torch.nn.GroupNorm 的计算示意图
num_groups = 2 # 要求 num_features 能被 num_groups 整除。1、2 或 4
gn = GroupNorm(
num_groups=num_groups, # 分组数
num_channels=feature_maps_batch.size(1), # 通道数(特征数)
eps=1e-05, # 分母修正项
affine=True # 是否需要 affine transform
)
output = gn(feature_maps_batch)
2.4.1 weight 和 bias 属性
print('GN weight shape: {}, GN bias shape: {}'.format(
gn.weight.size(), gn.bias.size()
))
# GN weight shape: torch.Size([4]), GN bias shape: torch.Size([4])
print(gn.weight)
# Parameter containing:
# tensor([1., 1., 1., 1.], requires_grad=True)
print(gn.bias)
# Parameter containing:
# tensor([0., 0., 0., 0.], requires_grad=True)
在 GN 中,weight 和 bias 为逐通道的,无 running_mean 和 running_var。
手动计算
对于 num_groups=2 时 batch 中的第一个 group
num_features_in_group = int(feature_maps_batch.size(1)/num_groups)
first_group = feature_maps_batch[:, :num_features_in_group, :, :]
out = (first_group - first_group.mean()) / (first_group.std(unbiased=False) + 1e-5)
print(out)
# tensor([[[[-1.8000, -1.0000],
# [-0.2000, 0.6000]],
#
# [[-1.0000, -0.2000],
# [ 0.6000, 1.4000]]],
#
#
# [[[-1.4000, -0.6000],
# [ 0.2000, 1.0000]],
#
# [[-0.6000, 0.2000],
# [ 1.0000, 1.8000]]]])




