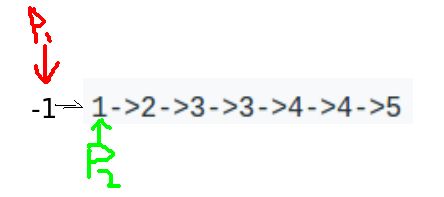一起来刷LeetCode呀～
一起来刷LeetCode呀～
- 1. 二分查找
- 2. 链表
- 3. 树
- 4. 字符串处理
- 5. DFS + 回溯
- 6. 滑动窗口、双指针、单调队列和单调栈
- 7. 基本数据结构
- 8. 动态规划
为找工作狂刷leetcode编程题。之前就乱刷，刷完就忘，现在一边看大佬 视频一边刷，并记录一下。
把题分类刷。
现在看到链表了，暂时先更新链表的
1. 二分查找
2. 链表
19. 删除链表倒数第N个节点
给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。
注意： 这里可能会删除头节点，涉及到头节点的删除需要定义一个虚拟的头节点接在它前面
思路：
- 初始化一个新的头节点，将链表头节点接在后面
- 定义两个指针， first 和 second指向头节点
- 让first指针先走n步
- 让first和second指针同时走，直到first指针走到最后一个节点, 此时second指针走到待删除节点前
- 删除待删节点：s->next = s->next->next;
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* res = new ListNode(-1);
res->next = head;
ListNode* p1 = res;
ListNode* p2 = res;
while(p1->next)
{
p1 = p1->next;
if(n <= 0)
{
p2 = p2->next;
}
n--;
}
p2->next = p2->next->next;
return res->next;
}
237. 删除链表中的节点
请编写一个函数，使其可以删除某个链表中给定的（非末尾）节点，你将只被给定要求被删除的节点。
void deleteNode(ListNode* node) {
node->val = node->next->val;
node->next = node->next->next;
}
83. 删除排序链表中的重复元素
给定一个排序链表，删除所有重复的元素，使得每个元素只出现一次。
ListNode* deleteDuplicates(ListNode* head) {
if(head == NULL)
return head;
ListNode* cur = head;
while(cur->next)
{
//当下一个节点与当前节点值重复则删除下一个节点
//若下一个节点与当前节点值不同，则移动到下一个节点
if(cur->next->val == cur->val)
cur->next = cur->next->next;
else
cur = cur->next;
}
return head;
}
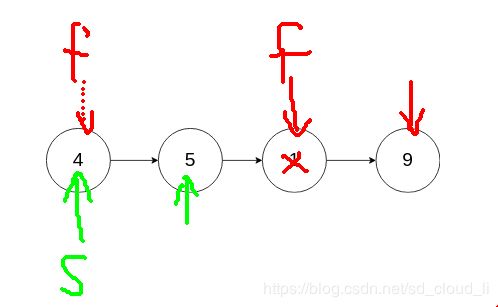
82. 删除排序链表中的重复元素 II
给定一个排序链表，删除所有含有重复数字的节点，只保留原始链表中 没有重复出现 的数字。
这题与上题类似，但是它是要把所有重复的点都删了，上一题是把重复的点变不重复，即保留一个。
注意：这里又涉及到删除头节点的问题，若开头的 几个节点重复，则需要删除头节点，所以要定义一个虚拟头节点。
思路(仅个人思路)：
- 定义一个虚拟头节点指向head
- 定义两个指针p1和p2分别指向虚拟头节点和头节点下一个
- 比较p1->next的值和p2->next的值，若不等，则两个指针同时后移，若相等则p2后移知道p2->next与p1->next不相等
- 此时p1到p2->next之间都是重复的，将其删除，即p1->next = p2->next
- 直到p2->next = NULL
ListNode* deleteDuplicates(ListNode* head) {
auto res = new ListNode(-1);
res->next = head;
auto p1 = res;
auto p2 = res->next;
while(p2 && p2->next)
{
if(p2->next->val != p1->next->val)
{
p1 = p1->next;
p2 = p2->next;
continue;
}
while(p2->next && p2->next->val == p1->next->val)
{
p2 = p2->next;
}
p1->next = p2->next;
p2 = p2->next;
}
return res->next;
}
61. 旋转链表
给定一个链表，旋转链表，将链表每个节点向右移动 k 个位置，其中 k 是非负数。
这题的意思就是把链表最后k个移到链表前面，所以要先找到倒数第k个节点，这和删除倒数第N个节点思路一样。
在这之前要注意，k可能是一个大于链表长度的数，所以要先对链表长度取模，那么就要先求链表长度。
- 扫描一遍链表，计算链表长度n，然后k=k%n
- 定义指针p1和p2， p1先走k步，然后一直走，直到p1指向最后一个节点，此时p2指向待旋转节点前一个节点
- 让p1指向头节点，令头节点为p2->next,再让p2->next = NULL
- 返回头节点
ListNode* rotateRight(ListNode* head, int k) {
if(!head) return NULL;
//第一步 求链表长度n，用k对n取模
ListNode* p = head;
int n = 0;
while(p)
{
p = p->next;
n++;
}
k = k%n;
if(k == 0)
return head;
auto* p1 = head, p2 = head;
while(k--) p1 = p1->next;
while(p1->next)
{
p1 = p1->next;
p2 = p2->next;
}
p1->next = head;
head = p2->next;
p2->next = NULL;
return head;
}
24. 两两交换链表中的节点
给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。
你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。
由于两两交换，头节点会变化，所以先建立虚拟节点。
思路：
- 先建一个虚拟头节点，定义指针p指向该头节点
- 当p->next和p->next->next存在 说明有节点要进行交换
- 定义a= p->next, b = a->next 交换a和b， 然后将p向后移动两位，重复3这个过程
ListNode* swapPairs(ListNode* head) {
ListNode* res = new ListNode(-1);
res->next = head;
auto p = res;
while(p->next && p->next->next)
{
auto a = p->next, b = a->next;
a->next = b->next;
b->next = a;
p->next = b;
p = p->next->next;
}
return res->next;
}
206. 反转链表
反转一个单链表。
定义指针p指向head, q指向p->next,
p, q 一直往后移，在过程中， 用o记录q->next, 然后q->next指向p
p = q, q = o
知道q->next指向NULL 说明q指向最后一个节点了
再让head指向NULL
返回q
ListNode* reverseList(ListNode* head) {
if(!head)
return head;
auto p = head, q = p->next;
while(q)
{
auto o = q->next;
q->next = p;
p = q;
q = o;
}
head->next = NULL;
return p;
}
160. 相交链表
编写一个程序，找到两个单链表相交的起始节点。
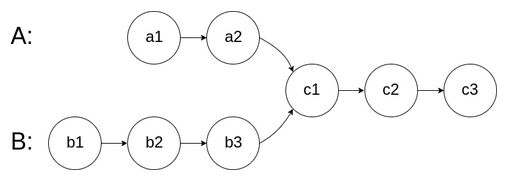
思路 ：
4. 定义两个指针q和p分别指向headA和headB
5. 若指针还未指向结尾的NULL, 则指针向后移动一位
6. 若指针指向NULL了则下一次指向另一个链表的头节点，即若p = NULL, 则p->next = headB, 若q = NULL, 则q->next = headA
7. 最终p和q相遇，要么指向第一个相交的节点，要么不相交，指向链表尾部的NULL.
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
auto p = headA, q = headB;
while(p != q)
{
if(p) p = p->next;
else p = headB;
if(q) q = q->next;
else q = headA;
}
return p;
}
3. 树
8.29更新
98. 验证二叉搜索树
给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
自上往下思路：
当前节点值为x
左子树和右子树里每个点都有一个取值范围
递归判断每个点是否在范围内
bool isValidBST(TreeNode* root) {
return dfs(root, INT_MIN, INT_MAX);
}
bool dfs(TreeNode* root, long long min, long long max)
{
if(!root) return true;
if(root->val < min || root->val > max) return false;
//1ll是将1强行转化为long long型 因为val可能会为INT_MAX 加1会溢出
return dfs(root->left, min, root->val - 1ll) && dfs(root->right, root->val + 1ll, max);
}
94. 二叉树的中序遍历
给定一个二叉树，返回它的中序 遍历。
借助栈来做。
先根节点入栈，若左子树不为空，则把左子节点入栈，直到左子树为空
把栈最后一位输出
若该节点有右子树，则右子节点入栈
然后再检测入栈的节点左子树是否为空，不为空则左子节点入栈直到左子树为空
然后取出栈顶元素
我感觉是刚开始碰到左子树不为空则一直入栈，为空则开始出栈
出栈后判断有无右子树，有则把右子树以同样的方式入栈， 无则继续出栈
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> s;
auto p = root;
while(p || !s.empty())
{
while(p)
{
s.push(p);
p = p->left;
}
p = s.top();
s.pop();
res.push_back(p->val);
p = p->right;
}
return res;
}
101. 对称二叉树
给定一个二叉树，检查它是否是镜像对称的。
就是判断左子树和右子树是否完全对称
- 两个根节点值要相等
- 左边的左子树和右边的右子树对称
- 左边的右子树和右边的左子树对称
- 递归法
bool isSymmetric(TreeNode* root) {
if(!root) return true;
return dfs(root->left, root->right);
}
bool dfs(TreeNode* p, TreeNode* q)
{
if(!p || !q) return !p && !q;
return p->val == q->val && dfs(p->left, q->right) && dfs(p->right, q->left);
}
- 迭代法
左子树是左中右顺序遍历
右子树是右中左顺序遍历
bool isSymmetric(TreeNode* root) {
if(!root) return true;
stack<TreeNode*> p, q;
auto l = root->left, r = root->right;
while(l || r || !p.empty() || !q.empty())
{
//当左边左子树和右边右子树同时存在时
//分别入栈， 直到最左边的节点
while(l && r)
{
p.push(l);
l = l->left;
q.push(r);
r = r->right;
}
if(l || r) return false;
l = p.top();
p.pop();
r = q.top();
q.pop();
//取出节点判断是否值相等
if(l->val != r->val)
return false;
l = l->right;
r = r->left;
}
return true;
}
105. 从前序与中序遍历序列构造二叉树
节点个数为n
前序遍历第一个点为根节点
中序遍历中找到根节点m
中序遍历根节点前面m-1的点为左子树， 后面n-m-1的点为右子树
然后对左子树重构，右子树重构就可以了
这是一个递归的过程
//map 与unordered_map区别： map自动排序， unordered_map不排序
//建一个hash表，记录中序遍历节点对应的索引，
//以便直接用前序遍历的第一个点找到中序遍历中的根节点
unordered_map<int, int> pos;
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
for(int i = 0; i < n; ++i)
pos[inorder[i]] = i;
//四个数代表前序与中序用于构建树的节点区间
return buildTree(preorder, inorder, 0, n-1, 0, n-1);
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder, int pl, int pr, int il, int ir)
{
if(pl > pr)
return NULL;
//创建根节点
int val = preorder[pl];
TreeNode* root = new TreeNode(val);
//找到中序遍历中的根节点
int k = pos[val]; //val这个值在inorder的索引
//分别构建左子树和右子树
//左子树的节点有k-il个 在前序中区间为 pl+1 ~ pl+k-il 在中序中区间为 il ~ k-1
//右子树的节点有ir-k个 在前序中区间为 pl+k-il+1 ~ pr 在中序中区间为 k+1 ~ ir
root->left = buildTree(preorder, inorder, pl + 1, pl + k - il, il, k - 1);
root->right = buildTree(preorder, inorder, pl + k - il + 1, pr, k + 1, ir);
return root;
}
二叉树的层次遍历
给定一个二叉树，返回其按层次遍历的节点值。 （即逐层地，从左到右访问所有节点）。
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int> > res;
if(!root) return res;
queue<TreeNode*> q;
q.push(root);
while(!q.empty())
{
int s = q.size();
vector<int> temp;
for(int i = 0; i < s; ++i)
{
TreeNode* node = q.front();
q.pop();
temp.push_back(node->val);
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
res.push_back(temp);
}
return res;
}
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
- 情况分析
- 根节点为空，或者p为根节点，或者q为根节点，则返回根节点
- 否则要么两个节点都包含在左子树或右子树，或者分别包含在左子树和右子树
若左边一个右边一个，则左右各返回一个，即左右均不为空此时返回root
若左边为空则说明都在右边，返回右边即可
若右边为空则说明都在左边， 返回左边即可
注： 不存在两边都为空的情况
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root || root == p || root == q)
return root;
auto left = lowestCommonAncestor(root->left, p, q);
auto right = lowestCommonAncestor(root->right, p, q);
if(!left) return right;
if(!right) return left;
return root;
}
543. 二叉树的直径
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。
递归时需要计算，从当前节点往左右两边走的最大值之和
左边最大值为左子树最大深度+1,右边最大值为右子树深度+1
int ans = 0;
int diameterOfBinaryTree(TreeNode* root) {
dfs(root);
return ans;
}
int dfs(TreeNode* root)
{
if(!root) return 0;
auto left = dfs(root->left);
auto right = dfs(root->right);
ans = max(ans, left + right);
return max(left + 1, right + 1);
}
124. 二叉树的最大路径和
给定一个非空二叉树，返回其最大路径和。
本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。
节点值之和最大
即每个节点向左走最大与向右走最大加上当前节点的值
过每个节点计算其向左走最大和向右走最大， 当最大为负的时候，则返回0表示不需要左边这条路
int ans = INT_MIN;
int maxPathSum(TreeNode* root) {
dfs(root);
return ans;
}
//返回从root向下走的最大值
int dfs(TreeNode* root)
{
if(!root)
return 0;
int left = dfs(root->left);
int right = dfs(root->right);
ans = max(ans, root->val + left + right);
return max(0, root->val + max(left, right));
}
173. 二叉搜索树迭代器
实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。
调用 next() 将返回二叉搜索树中的下一个最小的数。
借助栈中序遍历
class BSTIterator {
public:
stack<TreeNode*> stk;
BSTIterator(TreeNode* root) {
while(root)
{
stk.push(root);
root = root->left;
}
}
/** @return the next smallest number */
int next() {
auto p = stk.top();
stk.pop();
int res = p->val;
p = p->right;
while(p)
{
stk.push(p);
p = p->left;
}
return res;
}
/** @return whether we have a next smallest number */
bool hasNext() {
return !stk.empty();
}
};
297. 二叉树的序列化与反序列化
序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
注意： 一般情况下，前序遍历不能唯一确定一棵二叉树
前序遍历+中序遍历可以唯一确定一棵二叉树
但是这里用前序遍历可唯一确认，因为把NULL节点都加上了。
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
string res;
dfs1(root, res);
return res;
}
void dfs1(TreeNode* root, string& res)
{
if(!root)
{
res += "#,";
return;
}
res += to_string(root->val) + ',';
dfs1(root->left, res);
dfs1(root->right, res);
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
int u = 0;
return dfs2(data, u);
}
TreeNode* dfs2(string data, int& u)
{
if(data[u] == '#')
{
u += 2; //跳过#和,
return NULL;
}
//处理负数
int t = 0;
bool is_minus = false;
if(data[u] == '-')
{
is_minus = true;
u++;
}
while(data[u] != ',')
{
t = t * 10 + data[u] - '0';
u++;
}
u++; //指向了下一个数
if(is_minus) t = -t;
auto root = new TreeNode(t);
root->left = dfs2(data, u);
root->right = dfs2(data, u);
return root;
}
};
4. 字符串处理
8.30更新
38. 报数
报数序列是一个整数序列，按照其中的整数的顺序进行报数，得到下一个数。其前五项如下：
1
11
21
1211
111221
1 被读作 “one 1” (“一个一”) , 即 11。
11 被读作 “two 1s” (“两个一”）, 即 21。
21 被读作 “one 2”, “one 1” （“一个二” , “一个一”) , 即 1211。
每一行都是对前一行的报数，所以是一个数连续出现的次数加一个数字这样排列
我的思路：
先令count为1，从第2个数开始和前一个数比较，如果相同则count++并继续下一位，否则把count和前一个数字加在string后面，并令count为1。
注意，这样操作是把当前遍历到的数前面的数报了，当前没报，所以最后一位的时候要单独给添加进去。
第6行就为：
和1相同count++,直到2, 此时count为3
31 令count = 1
和2相同count++, 直到1, 此时count为2
22 令count = 1
此时已经到最后一位了，将count和数字添加
11
最终第6行为312211， 令上一行的vector为第6行的结果，然后计算第7行
string countAndSay(int n) {
string s = "1";
//每一层对上一层报数
for(int i = 0; i < n-1; ++i)
{
string ns = ""; //记录当前层报数结果
//从上一层第一个数开始
for(int j = 0; j < s.size(); ++j)
{
int k = j;
//如果相等则k++, 循环结束时有k-j个与s[j]相同的数
while(k < s.size() && s[k] == s[j]) k++;
ns += to_string(k - j) + s[j];
//下一次数数从s[k]开始，但是由于循环j每次都会加1， 所以这里要减1
j = k - 1;
}
s = ns;
}
return s;
}
8.31更新
49. 字母异位词分组
给定一个字符串数组，将字母异位词组合在一起。字母异位词指字母相同，但排列不同的字符串。
考察哈希表
如： eat, tea, ate这三个字符串排序后的字符串都为aet
那么可以定义一个unordered_map
时间复杂度，n为单词个数，m为单词平均长度
排序复杂度为 nmlogm, 哈希表插入 nm
总的时间复杂度为nmlogm + nm
vector<vector<string>> groupAnagrams(vector<string>& strs) {
int n = strs.size();
unordered_map<string, vector<string> > p;
for(auto str : strs)
{
string key = str;
sort(key.begin(), key.end());
p[key].push_back(str);
}
vector<vector<string> > res;
for(auto pi : p)
res.push_back(pi.second);
return res;
}
151. 翻转字符串里的单词
给定一个字符串，逐个翻转字符串中的每个单词。
大佬思路：
最原始字符串：
the sky is blue
在单词内部翻转:eht yks si eulb
整个字符串翻转:blue is sky the
对于空格处理： 将开始多余的空格压缩掉
string reverseWords(string s) {
int n = s.length(), k = 0;
for(int i = 0; i < n; ++i)
{
//跳过开头的空格
while(i < n && s[i] == ' ') i++;
if(i == n) break;
int j = i;
//找到当前字符串
while(j < n && s[j] != ' ') j++;
//翻转
reverse(s.begin() + i, s.begin() + j);
//上个单词后面加空格
if(k) s[k++] = ' ';
//将当前单词更新
while(i < j) s[k++] = s[i++];
}
//将末尾多余的删除
s.erase(s.begin() + k, s.end());
//翻转整个字符串
reverse(s.begin(), s.end());
return s;
}
165. 比较版本号
对应版本位字符串转换为数字，然后比较大小
提取对应版本位即定位’.’, 将其前面部分提取出来转换为数字(atoi)
int compareVersion(string version1, string version2) {
int i = 0, j = 0;
int len1 = version1.size(), len2 = version2.size();
//同时对两个字符串提取对应字符串
while(i < len1 || j < len2)
{
int x = i, y = j;
while(x < len1 && version1[x] != '.') x++;
while(y < len2 && version2[y] != '.') y++;
int a = x == i ? 0 : atoi(version1.substr(i, x - i).c_str());
int b = y == j ? 0 : atoi(version2.substr(j, y - j).c_str());
if(a > b) return 1;
if(a < b) return -1;
i = x + 1;
j = y + 1;
}
return 0;
}
929. 独特的邮件地址
每一个邮箱通过过滤都对应一个新邮箱，然后用哈希表存储新邮箱，返回哈希表的大小即可
过滤：
- 将本地名和域名分开，即定位’@'的位置，可以用find函数
- 将本地名进行过滤
1）碰到’+‘号则停止，后面的部分不要
2）碰到’.'号则跳过
int numUniqueEmails(vector<string>& emails) {
unordered_set<string> hash;
for(auto email : emails)
{
//找到@的位置
int at = email.find('@');
string name;
for(auto c : email.substr(0, at))
if(c == '+') break;
else if(c != '.') name += c;
string domain = email.substr(at + 1);
hash.insert(name + '@' + domain);
}
return hash.size();
}
5. 最长回文子串
暴力扫描，时间复杂度O(n^2)
string longestPalindrome(string s) {
string res;
int n = s.length();
//以每个字符为中心，向两边扫描
for(int i = 0; i < n; ++i)
{
//对于奇数回文串
for(int j = i, k = i; j >= 0 && k < n && s[k] == s[j]; --j, ++k)
if(k - j + 1 > res.size())
res = s.substr(j, k - j + 1);
//对于偶数回文串
for(int j = i, k = i + 1; j >= 0 && k < n && s[k] == s[j]; --j, ++k)
if(k - j + 1 > res.size())
res = s.substr(j, k - j + 1);
}
return res;
}
6. 之字形变换
找规律，之字形排列后，每一行都有等差数列，第一和最后一行都有一个等差数列，中间都是有两个等差数列交错，所以只要确定数列第一项和公差，这道题就出来了
string convert(string s, int numRows) {
if(numRows == 1) return s;
string res;
for(int i = 0; i < numRows; ++i)
{
if(!i || i == numRows - 1)
{
for(int j = i; j < s.size(); j += 2 * (numRows - 1))
res += s[j];
}
else
{
for(int j = i, k = 2 * (numRows - 1) - i; j < s.size() || k < s.size(); j += 2 * (numRows - 1), k += 2 * (numRows - 1))
{
if(j < s.size()) res += s[j];
if(k < s.size()) res += s[k];
}
}
}
return res;
}
3. 无重复的最长子串
以第i个字符为结尾，定义一个指针往前移动，直到有重复项，得到以s[i]为结尾的最长无重复字符串
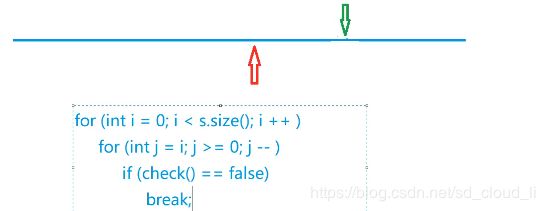
当绿色指针往后移动时，它所得到的红指针也一定不会往前动的.
int lengthOfLongestSubstring(string s) {
unordered_map<char, int> hash;
int res = 0;
for(int i = 0, j = 0; i < s.size(); ++i)
{
hash[s[i]]++;
while(hash[s[i]] > 1) hash[s[j++]]--;
res = max(res, i - j + 1);
}
return res;
}
代码是定义一个哈希表记录每一个字符的个数
红指针绿指针同时从0位置开始，红指针一直往前走，当碰到与绿指针相同的字符则绿指针往前走，并将记录该字符个数减一(使红绿指针之间每个字符记录个数都为1)
208. 实现Trie(前缀树)
插入：apple, appce, apda
先定义所需节点，每个节点最多有26个子节点，每个节点需要判断是否为单词结尾,并先定义一个根节点
class Trie {
public:
struct Node{
bool is_end;
Node* son[26];
Node()
{
is_end = false;
for(int i = 0; i < 26; ++i)
son[i] = NULL;
}
}*root;
/** Initialize your data structure here. */
Trie() {
root = new Node();
}
/** Inserts a word into the trie. */
void insert(string word) {
auto p = root;
for(auto c : word)
{
int u = c - 'a';
if(p->son[u] == NULL) p->son[u] = new Node();
p = p->son[u];
}
p->is_end = true;
}
/** Returns if the word is in the trie. */
bool search(string word) {
auto p = root;
for(auto c : word)
{
int u = c - 'a';
if(p->son[u] == NULL) return false;
p = p->son[u];
}
return p->is_end;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
auto p = root;
for(auto c : prefix)
{
int u = c - 'a';
if(p->son[u] == NULL) return false;
p = p->son[u];
}
return true;
}
};
273. 整数转换英文表示
这道题需要对数字进行分块，发现它是如下形式，3位一分，中间都是同种类型的描述
可以写个函数得到中间部分
string small[20] = {"Zero", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine", "Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"};
string decade[10] = {"", "", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"};
string big[4] = {"Billion", "Million", "Thousand", ""};
string numberToWords(int num) {
if(!num) return small[0];
string res;
for(int i = 1000000000, j = 0; i > 0; i /= 1000, j++)
{
if(num >= i)
{
res += get_part(num / i) + big[j] + ' ';
num %= i;
}
}
while(res.back() == ' ') res.pop_back();
return res;
}
string get_part(int num)
{
string res;
if(num >= 100)
{
res += small[num / 100] + " Hundred ";
num %= 100;
}
if(num == 0) return res;
if(num >= 20)
{
res += decade[num / 10] + ' ';
num %= 10;
}
if(num == 0) return res;
res += small[num] + ' ';
return res;
}
5. DFS + 回溯
9.2更新
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
循环的方法：
string chars[8] = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
vector<string> letterCombinations(string digits) {
if(digits.empty()) return vector<string>();
vector<string> state(1, "");
for(auto u : digits)
{
int n = u - '2';
vector<string> now;
for(auto c : chars[n])
for(auto s : state)
now.push_back(s + c);
state = now;
}
return state;
}
79. 单词搜索
给定一个二维网格和一个单词，找出该单词是否存在于网格中。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
也就是说对于一个单词，先找到它第一个字符，然后通过它的上下左右找下一个字符，并且同一个单元格内只能使用一次。
int m, n;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
bool exist(vector<vector<char>>& board, string word) {
if(board.empty() || board[0].empty())
return false;
m = board.size(), n = board[0].size();
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j)
if(dfs(board, i, j, word, 0))
return true;
return false;
}
bool dfs(vector<vector<char>>& board, int x, int y, string& word, int u)
{
if(board[x][y] != word[u]) return false;
if(u == word.size() - 1) return true;
board[x][y] = '.';
for(int i = 0; i < 4; ++i)
{
int a = x + dx[i], b = y + dy[i];
if(a >= 0 && a < m && b >= 0 && b < n)
if(dfs(board, a, b, word, u+1))
return true;
}
//感觉这里很巧妙，如果找到匹配就把它修改掉，避免下一次再找到它
//但是进行下一个搜索时如果没有找到匹配就要把修改的改回来，不然对后面搜索有影响
board[x][y] = word[u];
return false;
}
46. 全排列
给定一个没有重复数字的序列，返回其所有可能的全排列。
- 对数字枚举
int n;
vector<bool> st;
vector<vector<int> > ans;
vector<int> path;
vector<vector<int>> permute(vector<int>& nums) {
n = nums.size();
st = vector<bool>(n);
dfs(nums, 0);
return ans;
}
void dfs(vector<int>& nums, int u)
{
if(u == n)
{
ans.push_back(path);
return;
}
for(int i = 0; i < n; ++i)
if(!st[i])
{
st[i] = true;
path.push_back(nums[i]);
dfs(nums, u + 1);
path.pop_back();
st[i] = false;
}
}
- 对位置枚举
//对位置枚举
int n;
vector<bool> st;
vector<vector<int> > ans;
vector<int> path;
vector<vector<int>> permute(vector<int>& nums) {
n = nums.size();
st = vector<bool>(n); //标记每个位置是否被枚举
path = vector<int>(n); //每个排列的size都是n
dfs(nums, 0); //0代表第几个数字
return ans;
}
void dfs(vector<int>& nums, int u)
{
//如果已经是最后一个数字了，则将排列加入答案
if(u == n)
{
ans.push_back(path);
return;
}
//对于第i个位置
for(int i = 0; i < n; ++i)
if(!st[i])
{
st[i] = true;
path[i] = nums[u];
dfs(nums, u + 1);
st[i] = false;
}
}
47. 全排列Ⅱ
有重复数字的全排列
如果第一个1枚举到第5个位置，那第2个1则只能从第6个位置开始
如果是一个新的数字，则从0开始枚举，如果是重复的数字则从重复数字枚举的下一个位置开始枚举。
int n;
vector<vector<int> >ans;
vector<int> path;
vector<bool> st;
vector<vector<int>> permuteUnique(vector<int>& nums) {
n = nums.size();
st = vector<bool>(n);
path = vector<int>(n);
sort(nums.begin(), nums.end());
dfs(nums, 0, 0);
return ans;
}
void dfs(vector<int>& nums, int u, int start)
{
if(u == n)
{
ans.push_back(path);
return;
}
for(int i = start; i < n; ++i)
if(!st[i])
{
st[i] = true;
path[i] = nums[u];
int s = u + 1 < n && nums[u + 1] == nums[u] ? i + 1 : 0;
dfs(nums, u + 1, s);
st[i] = false;
}
}
78. 子集
给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
这道题可以用递归枚举做，还可以用二进制做！！！
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int> > res;
//2的n次方可以用位运算操作
for(int i = 0; i < 1 << nums.size(); ++i)
{
vector<int> now;
for(int j = 0; j < nums.size(); ++j)
//判断二进制第j位是否是1
if(i >> j & 1)
now.push_back(nums[j]);
res.push_back(now);
}
return res;
}
90. 子集Ⅱ
给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
先统计每个数字出现次数，然后统计有多少种方案。
vector<vector<int> > ans;
vector<int> path;
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
sort(nums.begin(), nums.end());
dfs(nums, 0);
return ans;
}
void dfs(vector<int>& nums, int u)
{
if(u == nums.size())
{
ans.push_back(path);
return;
}
//计算当前数字个数
int k = 0;
while(k + u < nums.size() && nums[k + u] == nums[u]) k++;
for(int i = 0; i <= k; ++i)
{
dfs(nums, u + k);
path.push_back(nums[u]);
}
//恢复现场
for(int i = 0; i <= k; ++i) path.pop_back();
}
216. 组合总和
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。
说明：
所有数字都是正整数。
解集不能包含重复的组合。
vector<vector<int> > ans;
vector<int> path;
vector<vector<int>> combinationSum3(int k, int n) {
dfs(k, 1, n);
return ans;
}
void dfs(int k, int start, int n)
{
if(!k)
{
if(!n)
ans.push_back(path);
return;
}
for(int i = start; i <= 9; ++i)
{
path.push_back(i);
dfs(k - 1, i + 1, n - i);
path.pop_back();
}
}
52. N皇后Ⅱ
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击(两个皇后不能在同一行同一列同一条斜线上)。
一次枚举每一行皇后的位置，
- 每一列只能有一个皇后 col[N]
- 每条斜线上只能有一个皇后 正斜线d[2N] 反斜线ud[2N]
vector<bool> col, d, ud;
int ans = 0, n;
int totalNQueens(int _n) {
n = _n;
col = vector<bool>(n);
d = ud = vector<bool> (n * 2);
dfs(0);//从第0行开始
return ans;
}
void dfs(int u)
{
if(u == n)
{
ans++;
return;
}
for(int i = 0; i < n; ++i)
{
if(!col[i] && !d[u + i] && !ud[u - i + n])
{
col[i] = d[u + i] = ud[u - i + n] = true;
dfs(u + 1);
col[i] = d[u + i] = ud[u - i + n] = false;
}
}
}
37. 解数独
编写一个程序，通过已填充的空格来解决数独问题。
一个数独的解法需遵循如下规则：
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 ‘.’ 表示。
从前往后枚举每个空格该填哪个数
状态： row[9][9] col[9][9] cell[3][3][9]
bool row[9][9] = {0}, col[9][9] = {0}, cell[3][3][9] = {0};
void solveSudoku(vector<vector<char>>& board) {
for(int i = 0; i < 9; i++)
for(int j = 0; j < 9; j++)
{
char c = board[i][j];
if(c != '.')
{
int t = c - '1';
row[i][t] = col[j][t] = cell[i / 3][j / 3][t] = true;
}
}
dfs(board, 0, 0);
}
bool dfs(vector<vector<char>>& board, int x, int y)
{
if(y == 9) x++, y = 0;
if(x == 9) return true;
if(board[x][y] != '.') return dfs(board, x, y + 1);
for(int i = 0; i < 9; ++i)
if(!row[x][i] && !col[y][i] && !cell[x / 3][y / 3][i])
{
board[x][y] = '1' + i;
row[x][i] = col[y][i] = cell[x / 3][y / 3][i] = true;
if(dfs(board, x, y + 1)) return true;
row[x][i] = col[y][i] = cell[x / 3][y / 3][i] = false;
board[x][y] = '.';
}
return false;
}
473. 火柴拼正方形
现在，你知道小女孩有多少根火柴，请找出一种能使用所有火柴拼成一个正方形的方法。不能折断火柴，可以把火柴连接起来，并且每根火柴都要用到。
输入为小女孩拥有火柴的数目，每根火柴用其长度表示。输出即为是否能用所有的火柴拼成正方形。
依次构造正方形的每条边
剪枝：
- 从大到小枚举所有边
- 每条边内部的木棒长度规定成从大到小
- 如果当前当前木棒拼接失败， 则跳过接下来所有长度相同的木棒
- 如果当前木棒拼接失败，且是当前边的第一个，则直接剪掉当前分支
- 如果当前木棒拼接失败，且是当前边的最后一个，则直接剪掉当前分支
vector<bool> st;
bool makesquare(vector<int>& nums) {
int n = nums.size();
int sum = 0;
for(auto u : nums) sum += u;
if(!sum || sum % 4) return false;
sort(nums.begin(), nums.end());
reverse(nums.begin(), nums.end());
st = vector<bool>(n);
return dfs(nums, 0, 0, sum / 4);
}
//u为第u条边 cur为当前拼接边长度
bool dfs(vector<int>& nums, int u, int cur, int length)
{
//第u条边拼接成功，开始下一条边拼接
if(cur == length) u++, cur = 0;
if(u == 4) return true;
for(int i = 0; i < nums.size(); ++i)
//如果当前木棒没有被选择，并且加上当前边不大于总边长则继续拼接
if(!st[i] && nums[i] + cur <= length)
{
st[i] = true;
if(dfs(nums, u, cur + nums[i], length)) return true;
st[i] = false;
//第一条边或最后一条边失败，则当前分支剪掉
if(!cur) return false;
if(cur + nums[i] == length) return false;
while(i + 1 < nums.size() && nums[i + 1] == nums[i]) i++;
}
return false;
}
6. 滑动窗口、双指针、单调队列和单调栈
9.03更新
167. 两数之和Ⅱ - 输入有序数组
给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。
vector<int> twoSum(vector<int>& numbers, int target) {
//vector res(2, -1);
for(int i = 0, j = numbers.size() - 1; j < numbers.size(); ++i)
{
while(j - 1 > i && numbers[i] + numbers[j] > target) j--;
if(numbers[i] + numbers[j] == target)
return {i + 1, j + 1};
}
return {-1, -1};
}
88. 合并两个有序数组
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i = m - 1, j = n - 1, k = m + n - 1;
while(i >= 0 && j >= 0)
{
if(nums1[i] >= nums2[j])
nums1[k--] = nums1[i--];
else
nums1[k--] = nums2[j--];
}
while(j >= 0) nums1[k--] = nums2[j--];
}
26. 删除排序数组中的重复项
给定一个排序数组，你需要在原地删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。
不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
int removeDuplicates(vector<int>& nums) {
if(nums.empty())
return 0;
int k = 1;
for(int i = 1; i < nums.size(); ++i)
{
if(nums[i] != nums[i-1])
nums[k++] = nums[i];
}
return k;
}
**76. 最小覆盖子串 **
给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字母的最小子串。
i和j都从前往后枚举，当在i位置找到j使j到i包含字符串T,如果i往后移动，j也一定是不往前移动的。
string minWindow(string s, string t) {
string res;
unordered_map<char, int> hash;
for(auto c : t) hash[c]++;
int cnt = hash.size();
for(int i = 0, j = 0, c = 0; i < s.size(); i++)
{
if(hash[s[i]] == 1) c++;
hash[s[i]]--;
while(hash[s[j]] < 0) hash[s[j++]]++;
if(c == cnt)
{
if(res.empty() || res.size() > i - j +1)
res = s.substr(j, i - j + 1);
}
}
return res;
}
32. 最长有效括号
当左括号多于右括号的情况，检测不出来，因为都是大于等于0 的，所以要倒着做一遍。
int work(string s)
{
int res = 0;
for(int i = 0, start = 0, cnt = 0; i < s.size(); ++i)
if(s[i] == '(')
{
cnt++;
}else
{
cnt--;
if(cnt < 0) start = i + 1, cnt = 0;
else if(!cnt) res = max(res, i - start + 1);
}
return res;
}
int longestValidParentheses(string s) {
//正着找一遍
int res = work(s);
//倒着找一遍
reverse(s.begin(), s.end());
for(auto &c : s) c ^= 1;
return max(res, work(s));
}
155. 最小栈
设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。
push(x) -- 将元素 x 推入栈中。
pop() -- 删除栈顶的元素。
top() -- 获取栈顶元素。
getMin() -- 检索栈中的最小元素。
class MinStack {
public:
/** initialize your data structure here. */
stack<int> s;
stack<int> min;
MinStack() {
}
void push(int x) {
s.push(x);
if(min.empty() || x <= min.top())
min.push(x);
}
void pop() {
if(s.top() == min.top())
min.pop();
s.pop();
}
int top() {
return s.top();
}
int getMin() {
return min.top();
}
};
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。
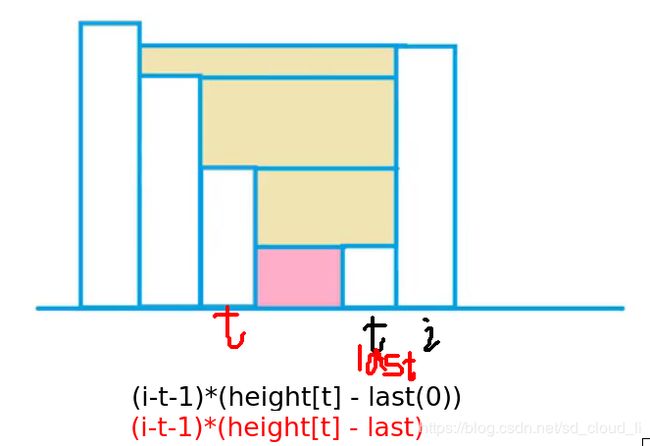
当前i,如果栈顶对应比当前小，则说明i和前面第一个比i处大的之间有坑，可以接雨水，
第一层记last = 0 然后计算雨水量，令last = t
第二层计算雨水量，
直到最后一层 last为小于i的最后一个
int trap(vector<int>& height) {
int res = 0;
stack<int> stk;
for(int i = 0; i < height.size(); ++i)
{
int last = 0;
while(stk.size() && height[stk.top()] <= height[i])
{
int t = stk.top();
stk.pop();
res += (i - t - 1) * (height[t] - last);
last = height[t];
}
if(stk.size())
res += (i - stk.top() - 1) * (height[i] - last);
stk.push(i);
}
return res;
}
84. 柱状图中最大的矩形
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
vector<int> left(n), right(n);
stack<int> stk;
//从左往右遍历单调栈，找每个柱左边比它最小的
for(int i = 0; i < n; ++i)
{
while(stk.size() && heights[stk.top()] >= heights[i]) stk.pop();
if(stk.empty()) left[i] = -1; //第一个柱状左边是-1
else left[i] = stk.top();
stk.push(i);
}
//右边则从右往左
while(stk.size()) stk.pop();
for(int i = n - 1; i >= 0; --i)
{
while(stk.size() && heights[stk.top()] >= heights[i]) stk.pop();
if(stk.empty()) right[i] = n; //最后一个柱状右边是n
else right[i] = stk.top();
stk.push(i);
}
int res = 0;
for(int i = 0; i < n; ++i)
res = max(res, heights[i] * (right[i] - left[i] - 1));
return res;
}
239. 滑动窗口最大值
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
/*暴力 O(nk)
vector res;
if(nums.empty()) return res;
for(int i = 0; i <= nums.size() - k; ++i)
{
int num = nums[i];
for(int j = 1; j < k; ++j)
num = max(num, nums[i + j]);
res.push_back(num);
}
return res;*/
//单调队列
vector<int> res;
//双向队列 队头队尾都能操作
deque<int> q;
for(int i = 0; i < nums.size(); ++i)
{
//队列不为空，i是要放入队尾的，如果队列元素已经有k个了，则队头元素要出列
//保持滑动窗口为以当前元素为结尾且个数 <= k
if(q.size() && i - k + 1 > q.front()) q.pop_front();
//把队列中在当前元素前且小于当前的元素删除
while(q.size() && nums[q.back()] <= nums[i]) q.pop_back();
q.push_back(i);//插入当前元素
if(i >= k - 1) res.push_back(nums[q.front()]); //加入结果
}
return res;
}
918. 环形子数组的最大和
int maxSubarraySumCircular(vector<int>& A) {
int n = A.size();
vector<int> sum(n * 2 + 1);
for(int i = 1; i <= n * 2; ++i)
sum[i] = sum[i - 1] + A[(i - 1) % n];
int res = INT_MIN;
deque<int> q;
q.push_back(0);
//用一个长度为n的滑窗，构造单调递增的队列
//每次用当前减去队头
for(int i = 1; i <= n * 2; ++i)
{
if(q.size() && i - n > q.front()) q.pop_front();
if(q.size()) res = max(res, sum[i] - sum[q.front()]);
while(q.size() && sum[q.back()] >= sum[i]) q.pop_back();
q.push_back(i);
}
return res;
}
7. 基本数据结构
9.4更新
这次题目主要涉及哈希表，并查集，堆的内容
1. 两数之和
用哈希表
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> p;
for(int i = 0; i < nums.size(); ++i)
{
if(p.count(target - nums[i]))
return {p[target - nums[i]], i};
p[nums[i]] = i;
}
return {-1, -1};
}
187. 重复的DNA序列
所有 DNA 由一系列缩写为 A，C，G 和 T 的核苷酸组成，例如：“ACGAATTCCG”。在研究 DNA 时，识别 DNA 中的重复序列有时会对研究非常有帮助。
编写一个函数来查找 DNA 分子中所有出现超多一次的10个字母长的序列（子串）。
思路
把所有长度为10的子串插入hash表计算次数
把次数大于等于2的字符串存储
vector<string> findRepeatedDnaSequences(string s) {
unordered_map<string, int> hash;
vector<string> res;
for(int i = 0; i + 10 <= s.size(); ++i)
{
string str = s.substr(i, 10);
hash[str]++;
if(hash[str] == 2)
res.push_back(str);
}
return res;
}
706. 设计哈系映射
题目中最多有10000个不同的value数
开一个长度为N= 20011的vector
vector
每个key都对应一个list
class MyHashMap {
public:
int N = 20011;
vector<list<pair<int, int>>> h;
/** Initialize your data structure here. */
MyHashMap() {
h = vector<list<pair<int, int>>>(N);
}
list<pair<int, int>>::iterator find(int key)
{
//为什么这里是这样，这是设计的存储方式
//只要设计的方式和后面存放和查找时的方式一样且有效都可以
int t = key % N;
for(auto it = h[t].begin(); it != h[t].end(); it++)
if(it->first == key)
return it;
return h[t].end();
}
/** value will always be non-negative. */
void put(int key, int value) {
auto it = find(key);
int t = key % N;
if(it == h[t].end()) h[t].push_back({key, value});
else it->second = value;
}
/** Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key */
int get(int key) {
auto it = find(key);
int t = key % N;
if(it == h[t].end()) return -1;
else return it->second;
}
/** Removes the mapping of the specified value key if this map contains a mapping for the key */
void remove(int key) {
auto it = find(key);
int t = key % N;
if(it != h[t].end()) h[t].erase(it);
}
};
652. 寻找重复子树
给定一棵二叉树，返回所有重复的子树。对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。
两棵树重复是指它们具有相同的结构以及相同的结点值。
可以把二叉树序列化变成一个字符串(前序遍历)，然后找重复子串
int cnt;
unordered_map<string, int> hash;
unordered_map<int, int> count;
vector<TreeNode*> ans;
vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
cnt = 0;
hash["#"] = ++cnt;
dfs(root);
return ans;
}
string dfs(TreeNode* root)
{
if(!root) return to_string(hash["#"]);
auto left = dfs(root->left);
auto right = dfs(root->right);
string tree = to_string(root->val) + ',' + left + ',' + right;
if(!hash.count(tree)) hash[tree] = ++cnt;
int t = hash[tree];
count[t]++;
if(count[t] == 2) ans.push_back(root);
return to_string(t);
}
560. 和为K的子数组
暴力想法：
计算以第i个数为尾的前面所有数的和S[i]
找到所有满足S[i] - S[j] = k(j < i)的个数
将这个满足式变式： S[j] = S[i] - k
即我走到第i个数了，计算了S[i],只要判断前面有多少个S[j] = S[i] - k, 就能得到以i为尾的满足题目要求的连续子数组个数;
所以开一个哈系表，存放S[j]及个数
当走到i时，看hash[S[i] - k]有多少个
int subarraySum(vector<int>& nums, int k) {
unordered_map<int, int> hash;
hash[0] = 1;
int res = 0;
for(int i = 0, sum = 0; i < nums.size(); ++i)
{
sum += nums[i];
res += hash[sum - k];
hash[sum]++;
}
return res;
}
547. 朋友圈
班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。
给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
这道题考察了并差集
最开始n个连通块，每个同学自己就是一个集合，然后对同学i和j判断是否在同一个集合，是的话就不用管，不是则合并且n–，即连通块减少1,最后还剩多少连通块即有多少个不交的朋友圈。
并查集找根节点的基本操作：如果节点x的父节点是本身，x即为x所在集合的根节点，否则找x的父节点的父节点重复操作直到某个节点的父节点是本身，则说明这个节点是根节点。
判断两个节点是否在同一个集合中即分别找到父节点看是否为同一个父节点。
vector<int> p;
//找根节点的基本操作
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int findCircleNum(vector<vector<int>>& M) {
int n = M.size();
for(int i = 0; i < n; ++i) p.push_back(i);
int res = n;
for(int i = 0; i < n; ++i)
for(int j = 0; j < i; ++j)
if(find(i) != find(j) && M[i][j] == 1)
{
//把i所在集合的根节点连接到j所在集合的根节点
p[find(i)] = find(j);
res--;
}
return res;
}
684. 冗余连接
在本问题中, 树指的是一个连通且无环的无向图。
输入一个图，该图由一个有着N个节点 (节点值不重复1, 2, …, N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间，这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ，满足 u < v，表示连接顶点u 和v的无向图的边。
返回一条可以删去的边，使得结果图是一个有着N个节点的树。如果有多个答案，则返回二维数组中最后出现的边。答案边 [u, v] 应满足相同的格式 u < v。
并查集
把边连接的两个节点所在集合合并
如果i和j已经在一个集合里了说明当前这条边是多余的
而且当发现多余的边，则说明这是最后一条多余的边，即需要输出的答案
vector<int> p;
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
for(int i = 0; i <= n; i++) p.push_back(i);
for(auto e : edges)
{
int a = e[0], b = e[1];
if(find(a) == find(b)) return {a, b};
p[find(a)] = find(b);
}
return {-1, -1};
}
692. 前k个高频单词
给一非空的单词列表，返回前 k 个出现次数最多的单词。
返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率，按字母顺序排序。
目标：找到出现次数最多的k个单词
用小根堆维护出现次数最多的k个单词
先用hash表存放单词出现频数
用优先队列(默认)来构建小根堆，priority_queue
为什么是最小根而不是最大根
如果是最大根，则直接存放频数和单词，如果频数相同的情况，则比较单词的字典序，字典序大的优先，而题目的结果字典序是由小到大，所以这里不能直接这样
构建最小堆，把频数变为相反数，越小则频数越大，而频数相同时，也满足字典序先小的。
vector<string> topKFrequent(vector<string>& words, int k) {
unordered_map<string, int> hash;//存每个单词出现的次数
typedef pair<int, string> PIS;
priority_queue<PIS> heap;
for(auto word : words) hash[word]++;
for(auto item : hash)
{
PIS t(-item.second, item.first);
heap.push(t);
if(heap.size() > k) heap.pop();//小根堆，把最大的删除，即出现频数最低的
}
vector<string> res(k);
for(int i = k - 1; i >= 0; --i)
{
res[i] = heap.top().second;
heap.pop();
}
return res;
}
295. 数据流的中位数
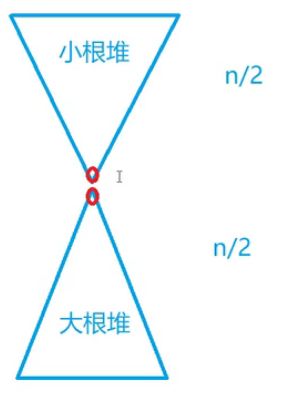
维护两个堆，一个大根堆一个大根堆，使两个堆元素个数相差不大于1
其中小根堆都大于等于大根堆
所以小根堆里top元素最大，大根堆里top元素最小，这也方便访问读取
插入：如果元素x比小根堆top小则插入小根堆， 比大根堆top大则插入大根堆
如果两个堆元素个数相等，则中位数为(大根top+小根top)/2
如果两个堆元素个数不同，则输出元素个数大的堆的top
class MedianFinder {
public:
priority_queue<int, vector<int>, greater<int>> up;//大根堆
priority_queue<int> down;//小根堆
/** initialize your data structure here. */
MedianFinder() {
}
void addNum(int num) {
//维护大根堆元素个数大于等于小根堆
//并且小根堆元素都比大根堆大
if(down.empty() || num > down.top()) up.push(num);
else
{
down.push(num);
up.push(down.top());
down.pop();
}
//维护两个堆元素数量差不大于1
if(up.size() > down.size() + 1)
{
down.push(up.top());
up.pop();
}
}
double findMedian() {
if(down.size() == up.size()) return (down.top() + up.top()) / 2.0;
else return up.top();
}
};
352. 将数据流变为多个不相交的区间
需要功能：排序，方便读取区间端点值
我的想法：进来一个num,就添加一个[num,num]区间，然后自动排序，然后判断区间是否合并
大佬思想：
用平衡树来维护所有区间
map
对于： [1,2], [4,7], [9,9]有：
R[1] = 2, R[4] = 7, R[9] = 9;
L[2] = 1, L[7] = 4, L[9] = 9;
当插入x 判断是否存在以x-1为右端点的区间，以及以x+1为左端点的区间
即L = x-1, R = x+ 1;
- 若x 已经插入过，则跳过，啥都不做
- 左右都存在，三个区间合并
- 左边存在，x与左边合并
- 右边存在，x与右边合并
- 都不存在 则[x,x]
class SummaryRanges {
public:
map<int, int> L, R;
/** Initialize your data structure here. */
SummaryRanges() {
}
void addNum(int x) {
if(L.size())
{
auto it = L.lower_bound(x); //找比x大的最小值 即找区间的端右点
if(it != L.end() && it->second <= x) return; //端点存在 且该区间的左端点<=x说明x已经包含在区间
}
int left = L.count(x - 1), right = R.count(x + 1);
if(left && right)
{
R[L[x - 1]] = R[x + 1];
L[R[x + 1]] = L[x - 1];
L.erase(x - 1), R.erase(x + 1);
}
else if(left)
{
R[L[x - 1]] = x;
L[x] = L[x - 1];
L.erase(x - 1);
}
else if(right)
{
L[R[x + 1]] = x;
R[x] = R[x + 1];
R.erase(x + 1);
}
else
{
R[x] = L[x] = x;
}
}
vector<vector<int>> getIntervals() {
vector<vector<int>> res;
for(auto item : R)
res.push_back({item.first, item.second});
return res;
}
};
8. 动态规划
9.5更新
53. 最大子序和
给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
以nums[i]结尾的最大子数组和为以nums[i-1]为结尾的最大子数组和加上nums[i]
int maxSubArray(vector<int>& nums) {
int res = INT_MIN, sum = 0;
for(int i = 0; i < nums.size(); ++i)
{
sum = max(0, sum);//如果前面的和小于0了，再加上当前数则比当前数还小
sum += nums[i];//以i结尾的子数组和最小为以i-1结尾子数组和最小加上nums[i]
res = max(res, sum);
}
return res;
}
120. 三角形最小路径和
给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
从后往前
从倒数第2行（第三行）开始，
如果最后通过6这个点一定会选择1
如果最后通过5一定会选择1
如果最后通过7一定会选择3
得到新的最后一行[7, 6, 10]
第二行
3选择6
4选择10
[9, 14]
第一行
2选择9
最后得到11
从前往后
第二行
3+2=5
4+2=6
[5,6]
第三行
6+5=11
5+5=10, 5+6=11, 选10 如果过5这个点，前面有两条路，一定选最小的那条
7+6 = 13
[11,10,13]
第四行
4+11 = 15
1+11 = 12， 1+10=11, 选11
8+10=18,8+13=21,选18
3+13=16
最后选最后一行最小的
int minimumTotal(vector<vector<int>>& triangle) {
int n = triangle.size();
vector<int> f;
f.assign(triangle[n-1].begin(), triangle[n-1].end());
for(int i = n - 2; i >= 0 ; --i)
for(int j = 0; j < triangle[i].size(); ++j)
f[j] = min(triangle[i][j] + f[j], triangle[i][j] + f[j + 1]);
return f[0];
}
//f的变化为
//[4 1 8 3] -> [7 6 10 3] -> [9 10 10 3] -> [11 10 10 3]
//从下往上不用担心数组长度的问题，每上一层都抛弃了一个位置，最后到第一层时就只需要f[0]
63. 不同路径 II
从起点开始，判断当前点是否可到达，
对于边缘上的点 即i == 0 || j == 0
到达当前点路径为到达左侧点路径（j== 0）或到达上方点路径(i==0)
对于非边缘的点 即i>0 && j >0
若到达当前点路径为向右或向下的路径之和
若不可到达则为0
到达当前点的路径只与上方和左侧到达路径相关
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size(), n = obstacleGrid[0].size();
vector<vector<long long>> res(m, vector<long long>(n));
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; ++j)
{
if(obstacleGrid[i][j]) continue;
if(!i && !j) res[i][j] = 1;
if(i) res[i][j] += res[i - 1][j];
if(j) res[i][j] += res[i][j - 1];
}
}
return res[m - 1][n - 1];
}
91. 解码方法
用f[i]表示以s[i]结尾得到解码的字符串集合，有两种形式，最后一个字母是一位数和最后一个字母是两位数，最后是一位数则情况等于f[i-1]的数量
最后一位是两位数则情况等于f[i-2]的数量
如果s[i]是0的话只能组成两位数
int numDecodings(string s) {
if(s[0] == '0') return 0;
int n = s.size();
vector<int> f(n + 1);
f[0] = 1;
for(int i = 1; i <= n; ++i)
{
if(s[i - 1] != '0') f[i] = f[i - 1];
if(i >= 2)
{
int t = (s[i - 2] - '0') * 10 + s[i - 1] - '0';
if(t >= 10 && t <= 26) f[i] += f[i - 2];
}
}
return f[n];
}
198. 打家劫舍
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。
如果我当前不选，则前一个可能选也可能不选
如果我当前选， 则前一个只能不选
最后答案在max(f[n - 1], g[n - 1]);
int rob(vector<int>& nums) {
int n = nums.size();
vector<int> f(n + 1), g(n + 1);
for(int i = 1; i <= n; ++i)
{
f[i] = max(f[i - 1], g[i - 1]);
g[i] = f[i - 1] + nums[i - 1];
}
return max(f[n], g[n]);
}
300. 最长上升子序列
给定一个无序的整数数组，找到其中最长上升子序列的长度。
以当前数结尾的子序列最长长度为 以比它小的数子序列最长的加1
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
vector<int> f(n, 1);
for(int i = 0; i < n; ++i)
for(int j = 0; j < i; ++j)
if(nums[i] > nums[j])
f[i] = max(f[i], f[j] + 1);
int res = 0;
for(int i = 0; i < n; ++i)
res = max(res, f[i]);
return res;
}
72. 编辑距离
给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作：
插入一个字符
删除一个字符
替换一个字符
好难呀这道题= _ =！
如果当前执行insert操作，则W1的前i与W2的前j-1已经改好了
则f[i,j] = f[i, j - 1] + 1
如果当前执行delete操作，则W1的前i-1与W2的前j已经改好了
则f[i,j] = f[i- 1, j] + 1
如果当前执行replace操作，则W1的前i-1与W2的前j-1已经改好了
且Wi的第i与W2的第j不相同，不然白费一步替换
则f[i,j] = f[i- 1, j - 1] + 1
Wi的第i与W2的第j相同
则f[i, j] = f[i - 1, j - 1]
int minDistance(string word1, string word2) {
int n = word1.size(), m = word2.size();
vector<vector<int>> f(n + 1, vector<int>(m + 1));
for(int i = 0; i <= n; ++i) f[i][0] = i;
for(int i = 0; i <= m; ++i) f[0][i] = i;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <=m; ++j)
{
f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;
f[i][j] = min(f[i][j], f[i - 1][j - 1] + (word1[i - 1] != word2[j - 1]));
}
return f[n][m];
}
518. 零钱兑换 II
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
f[i, j]表示由前i种硬币凑出总钱数为j的方案数
则考虑当第i种硬币凑多少时它与前面状态的关系
当第i中硬币凑t个时，f[i, j] = f[i - 1, j - t * coins[i]]
c = coins[i], 则
f[i, j] = f[i - 1, j] + f[i - 1, j - c] + f[i - 1, j - 2c] + ... + f[i - 1, j - kc]
f[i, j - c] = f[i - 1, j - c] + f[i - 1, j - 2c] + ... + f[i - 1, j - kc]
经过替换得到
f[i, j] = f[i - 1, j] + f[i, j - c];
第二为维只与j和j前面的有关，可以优化为1维的
f[j] = f[j] + f[j - c];
int change(int m, vector<int>& coins) {
int n = coins.size();
vector<int> f(m + 1);
f[0] = 1;
for(auto c : coins)
for(int j = c; j <= m; j++)
f[j] += f[j - c];
return f[m];
}
664. 奇怪的打印机
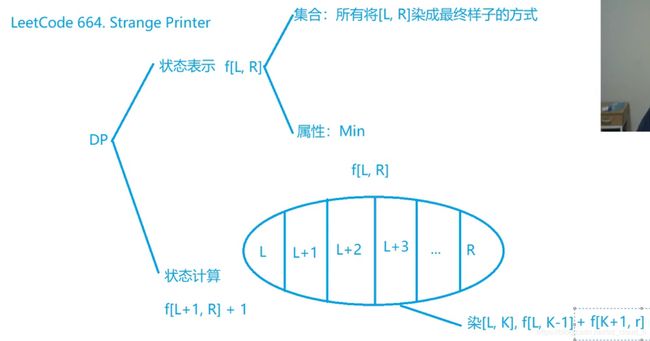
int strangePrinter(string s) {
int n = s.size();
if(n == 0)
return 0;
vector<vector<int>> f(n + 1, vector<int>(n + 1));
for(int len = 1; len <= n; len++)
for(int l = 0; l + len - 1 < n; l++)
{
int r = l + len - 1;
f[l][r] = f[l + 1][r] + 1;
for(int k = l + 1; k <= r; k++)
if(s[k] == s[l])
f[l][r] = min(f[l][r], f[l][k - 1] + f[k + 1][r]);
}
return f[0][n - 1];
}
10. 正则表达式匹配
给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。
说明:
s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。
注： 由题目意思*和其前面的字符是绑定在一起的，表示前面那个字符重复任意次
比如a* 可以表示为空或者a 或 aa ...
f[i, j]表示s的前i个字母和p的前j个字母受否匹配
1. p[j] != '*', f[i, j] = f[i - 1, j - 1] && (s[i]和p[j]匹配)
2. p[j] == '*', 需要枚举*表示多少个字母
f[i][j] = f[i, j - 2] || f[i - 1, j - 2] && (s[i]和p[j - 1]匹配) || f[i - 2, j - 2] (s[i - 1] == s[i] 匹配 p[j - 1])
bool isMatch(string s, string p) {
int n = s.size(), m = p.size();
s = ' ' + s;
p = ' ' + p;
vector<vector<bool>> f(n + 1, vector<bool>(m + 1));
for(int i = 0; i <= n; ++i)
for(int j = 0; j <= m; ++j)
{
if(!i && !j) f[i][j] = true;//开头的空格肯定匹配
if(j + 1 <= m && p[j + 1] == '*') continue;
if(p[j] != '*')
{
if(p[j] == '.' || s[i] == p[j])
if(i > 0 && j > 0)
f[i][j] = f[i - 1][j - 1];
}
else
{
if(j >= 2) f[i][j] = f[i][j - 2];
if(i > 0 && j >= 1)
{
if(p[j - 1] == '.' || s[i] == p[j - 1])
if(f[i - 1][j])
f[i][j] = true;
}
}
}
return f[n][m];
}