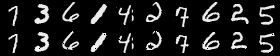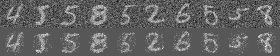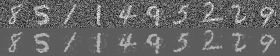漫谈autoencoder：降噪自编码器/稀疏自编码器/栈式自编码器（含tensorflow实现）

0. 前言

  在非监督学习中，最典型的一类神经网络莫过于autoencoder(自编码器)，它的目的是基于输入的unlabeled数据 X={x(1),x(2),x(3),...} X = { x ( 1 ) , x ( 2 ) , x ( 3 ) , . . . } ，通过训练得到数据的一个降维特征表达 H={h(1),h(2),h(3),...} H = { h ( 1 ) , h ( 2 ) , h ( 3 ) , . . . } 。以图像识别为例，隐层 H H 会提取出图像的边角，将这种更为抽象的特征作为后续的多层感知网络的输入，可以更好地表达输入图像，在图像分类等任务上获得更好的性能。
  从最原始的自编码器衍生出很多不同的种类：
   - 降噪自编码器，接受加噪的输入来进行训练
   - 稀疏自编码器，对隐层的激活输出进行正则，同一时间只有部分隐层神经元是活跃的
   - 栈式自编码器，级联多个自编码器，逐层提取抽象特征

1. 自编码器

1.1 定义

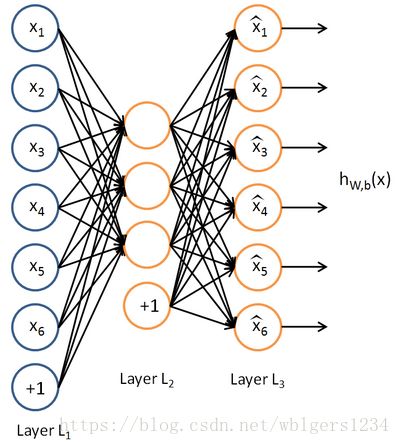
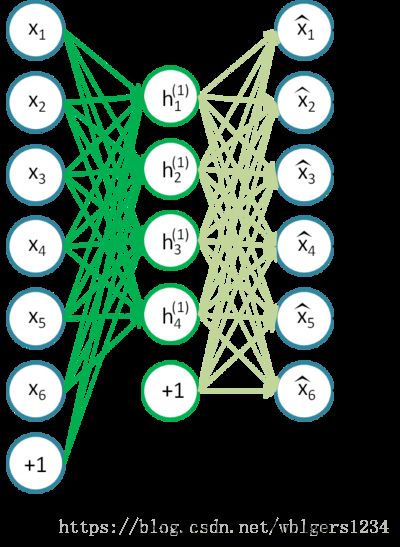
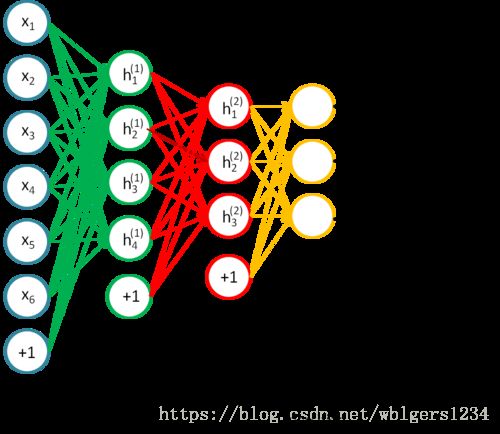
   自编码器分为两个部分，编码器encoder和解码器decoder。一个单隐层的AE的网络结构如下图所示：

   从上图可以看到，自编码器输出层的节点数与输入层相等，训练这个网络以期望得到近似恒等函数，以下分别对encoder/decoder以及损失函数进行表示：
  编码器：

h=σ(Wx+b) h = σ ( W x + b )

  解码器：

x^=σ(W′h+b′) x ^ = σ ( W ′ h + b ′ )

  损失函数：

{W,b,W′,b′}=argminLoss(x,x′)=||x−x′||2 { W , b , W ′ , b ′ } = a r g m i n L o s s ( x , x ′ ) = | | x − x ′ | | 2

1.2 tensorflow实现

  我们利用tensorflow实现一个自编码器，在MNIST数据库上进行测试，并且可视化输入图片和恢复后(reconstruction)图片的对比。选用激活函数为relu，设置隐层节点数为500，具体设置如下：

training_epochs = 20
batch_size = 128
display_step = 1

corruption_level = 0
sparse_reg = 0

#
n_inputs = 784
n_hidden = 500
n_outputs = 10
ae = Autoencoder(n_layers=[n_inputs, n_hidden],
                          transfer_function = tf.nn.relu,
                          optimizer = tf.train.AdamOptimizer(learning_rate = 0.001),
                          ae_para = [corruption_level, sparse_reg])

  下图是在测试集上对比输入和恢复的图片：

  可以从上图看到，在测试数据通过自编码器完成恢复的效果很好，图像也很清晰，可以认为是几乎完美的重构。为了和下一节的降噪自编码器进行比较，我们尝试在测试数据中加入一些高斯白噪声，以此来评估一下自编码器的抗噪性能。

batch_xs, _ = mnist.test.next_batch(n)
batch_xs += np.random.normal(loc=0, scale=0.3, size=batch_xs.shape)

  同样的在测试集上对比输入和恢复的图片如下图，可以看到自编码器有微弱的抗噪能力，但是不明显。

2. 降噪自编码器

2.1 定义

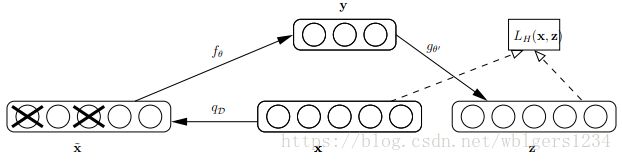
  和自编码器不同的是，降噪自编码的训练过程中，输入的数据有一部分是“损坏”的，DAE(Denoising Autoencoder)的核心思想是，一个能够从中恢复出原始信号的神经网络表达未必是最好的，能够对“损坏”的原始数据编码、解码，然后还能恢复真正的原始数据，这样的特征才是好的。在论文“Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion”中，阐述了DAE的原理，如下图所示：

  对于输入的数据 x x 按照 qD q D 分布加入进行加噪“损坏”，从图式可以看出，这个加噪过程是按照一定的概率将输入层的某些节点清0，然后将 x^ x ^ 作为自编码器的输入进行训练。除了对输入层数据的处理不同，其余部分DAE与AE完全类似。

2.2 tensorflow实现

  在用tensorflow实现的过程中，我们用dropout来完成这个加噪“损坏”过程。Dropout是指在模型训练时随机让网络某些隐含层节点的权重不工作，类似的，我们将dropout作用在输入层而不是隐层，就可以完成对输入层数据按照一定概率清0的操作。代码实现如下：

self.x = tf.placeholder(tf.float32, [None, self.n_layers[0]])
self.keep_prob = tf.placeholder(tf.float32)

h = tf.nn.dropout(self.x, self.keep_prob)

  在MNIST的训练集上对降噪自编码器进行训练，同样对加入高斯白噪声的测试数据进行编码解码恢复，对比输入和恢复的图片如下图所示，可以看到降噪自编码器相比自编码器有更好的抗噪能力，恢复的图片更清晰。

2.3 可视化特征提取

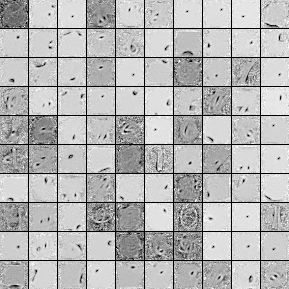
  将编码器的输入层与隐层之间的权重矩阵 W W 进行可视化，降噪自编码器的特征图显示为：

  作为对比，原始的自编码器的特征图显示为：

  从以上两幅特征图对比可以看出，降噪自编码器确实在训练后学习到了有效的特征提取，例如手写体数字的”转角”，这类特征更有代表性。

3. 稀疏自编码器

3.1 定义

  一般来说，自编码器的隐层节点数小于输入层的节点数，即在训练过程中，自编码器倾向于去学习数据内部的规律，例如相关性，那么自编码器学习的结果很可能类似于PCA，得到的是输入数据的一个降维表示。
  那如果我们设定隐层节点数大于输入层节点数，同时又想得到输入数据内一些有趣的结构和规律。我们给自编器加上一个稀疏性的限制，即在同一时间，只有某些隐层节点是“活跃”的，这样整个自编码器就变成稀疏的。
  假设隐层激活函数采用的是sigmoid，那么隐层输出为1代表这个节点很”活跃”，隐层输出为0代表这个节点”不活跃”。基于此，我们引入KL离散度来衡量某个隐层节点的平均激活输出和我们设定的稀疏度 ρ ρ 之间的相似性：

KL(ρ||ρ^j)=ρlogρρ^j+(1−ρ)log1−ρ1−ρ^j K L ( ρ | | ρ ^ j ) = ρ l o g ρ ρ ^ j + ( 1 − ρ ) l o g 1 − ρ 1 − ρ ^ j

  其中 ρ^j=1m∑i=1m[a(2)jx(i)] ρ ^ j = 1 m ∑ i = 1 m [ a j ( 2 ) x ( i ) ] ， m m 为训练样本的个数， a(2)jx(i) a j ( 2 ) x ( i ) 为隐层第 j j 个节点对 i i 个样本的响应输出。一般来说我们设定稀疏系数 ρ=0.05或0.1 ρ = 0.05 或 0.1 。KL离散度越大代表 ρ ρ 和 ρ^j ρ ^ j 之间相差越大，KL离散度等于0代表两者完全相等 ρ=ρ^j ρ = ρ ^ j 。
  因此，我们可以将KL离散度作为正则项加入到损失函数中，以此对整个自编码器网络的稀疏行进行约束：

Jsparse(W,b)=J(W,b)+β∑j=1s2KL(ρ||ρ^j) J s p a r s e ( W , b ) = J ( W , b ) + β ∑ j = 1 s 2 K L ( ρ | | ρ ^ j )

3.2 tensorflow实现

  在loss函数中加入正则项：

self.sparsity_level = 0.1

if self.sparse_reg == 0:
    self.cost = 0.5 * tf.reduce_sum(tf.pow(tf.subtract(self.reconstruction, self.x), 2.0))
else:
    self.cost = 0.5 * tf.reduce_sum(tf.pow(tf.subtract(self.reconstruction, self.x), 2.0))+\
                self.sparse_reg * self.kl_divergence(self.sparsity_level, self.hidden_encode[-1])

def kl_divergence(self, p, p_hat):
    return tf.reduce_mean(p * tf.log(tf.clip_by_value(p, 1e-8, tf.reduce_max(p)))
                          - p * tf.log(tf.clip_by_value(p_hat, 1e-8, tf.reduce_max(p_hat)))
                          + (1 - p) * tf.log(tf.clip_by_value(1-p, 1e-8, tf.reduce_max(1-p)))
                          - (1 - p) * tf.log(tf.clip_by_value(1-p_hat, 1e-8, tf.reduce_max(1-p_hat))))

  下图的运行结果是稀疏自编器通过训练学习到的特征显示：

  从上图确实看不大出，稀疏自编码器提取的特征有什么有意思的部分，但是对于加噪输入图像的去噪还是很有效果，见下图所示测试集上对比输入和恢复的图片：

4. 栈式自编码器

  顾名思义，栈式自编码器就是多个自编码器级联，以完成逐层特征提取的任务，最终得到的特征更有代表性，并且维度很小。
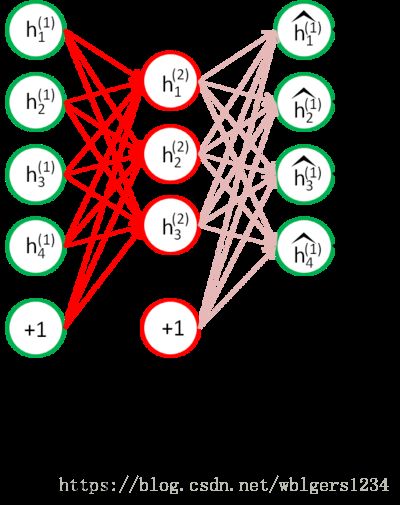
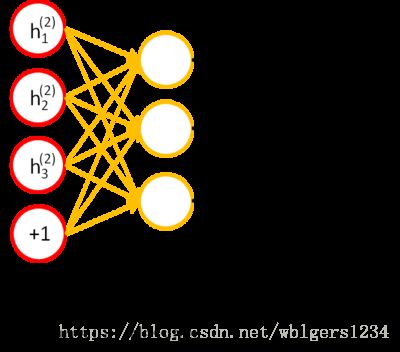
  栈式自编码器的训练过程是，n个AE按顺序训练，第1个AE训练完成后，将其编码器的输出作为第2个AE的输入，以此类推。最后得到的特征作为分类器的输入，完成最终的分类训练。如下四幅图所示：

  在逐层训练结束后，还需要一个微调过程(Fine tuning)。大意如下：逐层训练后，每层AE的权重和softmax分类层的权重已经有一个pretrain的值，此时，我们再将整个网络连接起来，用数据进行一次训练，让每层的权重参数同时得到改善。
  第一层降噪自编码器通过训练学习到的特征显示如下图：

  第二层降噪自编码器通过训练学习到的特征显示如下图：

  为了比较分类性能，我们对比降噪自编码器和栈式自编码器，在MNIST测试集上进行分类测试，分类的准确度对比如下。可以看到栈式自编码器的分类准确度要好于单个的降噪自编码器。

降噪自编码器
Accuracy on the test set:
0.9634

栈式降噪自编码器
Accuracy on the test set:
*************************Softmax*****************************
Test accuracy before fine-tune
0.7213
*************************Fine tune*****************************
0.9681

5. 项目地址

https://github.com/wblgers/tensorflow_stacked_denoising_autoencoder

代码可以直接运行，注释还待完善，喜欢的话可以点个star.

6. 参考资料

(1) https://en.wikipedia.org/wiki/Autoencoder
(2) http://deeplearning.stanford.edu/wiki/index.php/Stacked_Autoencoders
(3) http://ufldl.stanford.edu/tutorial/unsupervised/Autoencoders/
(4) https://www.cnblogs.com/tornadomeet/p/3261247.html