虚树-树上动态规划的利器

虚树

---

问题引入

在一类树上动态规划问题中,题目给出的询问往往包含树上的很多各节点,并保证总的点数规模小于某个值.

如果我们直接在整颗树上进行 dp d p 的话,时间复杂度与询问的次数有关,这显然是不可接受的,如果我们可以找到一种动态规划的方法,使其时间复杂度与询问中点的实际规模相关就好了.

于是虚树应运而生.

虚树概念

虚树即是一颗虚拟构建的一棵树,这个树只包含关键点以及关键 lca l c a 的点,而其他不影响虚树结构的点和边都相当于进行了路径压缩,整颗虚树的规模不会超过 关键点 关 键 点 数目的两倍.

举个栗子

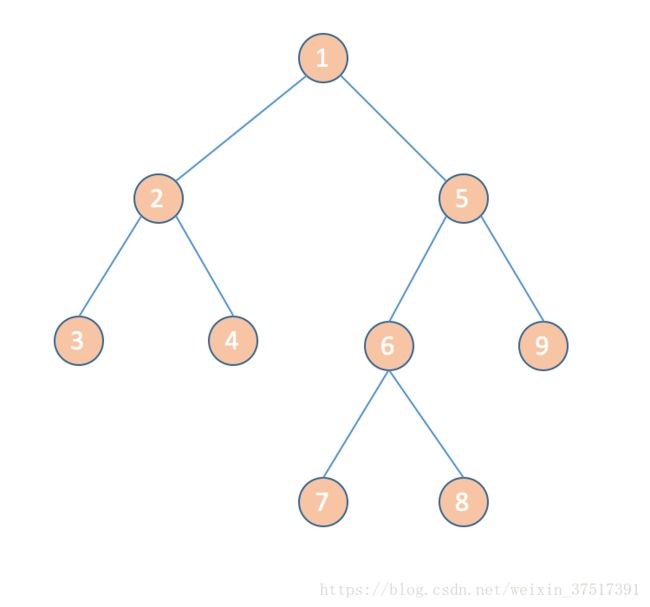
原树

---

虚树

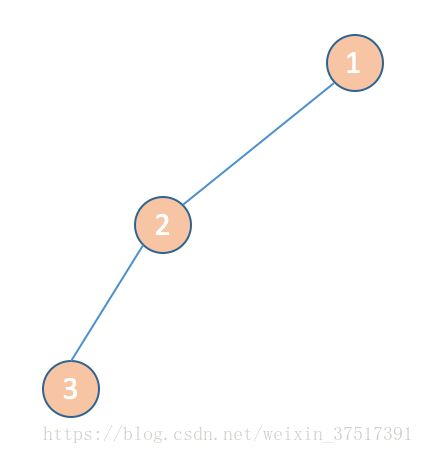
包含关键点 1 2 3的虚树

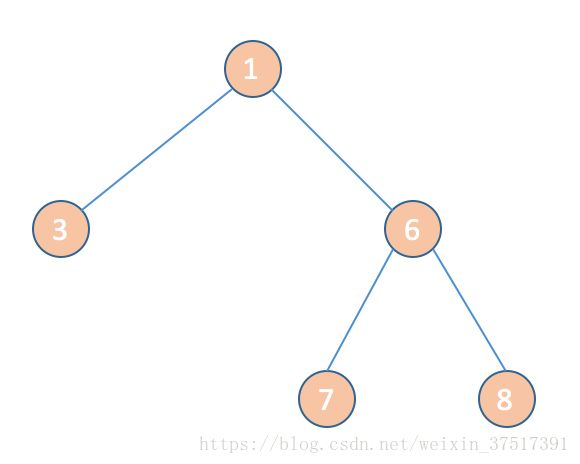
包含关键点 1 3 7 8 的虚树

其中6是关键 lca l c a 节点

很显然,其他不是那么关键的点及边形成的路径我们都将他们压缩到了一条边,例如在第二个虚树中,我们相当于把 1−6 1 − 6 的路劲压缩到了边 1−6 1 − 6 中,而 9 9 号节点这种非关键点我们直接扔掉了,因为我们在 dp d p 的时候不会用到 9 9 号点.

虚树构建

预处理我们对整颗树得到dfs序列(即前序遍历),记为 dfn[u] d f n [ u ] .

我们使用一个栈,从栈顶到栈底的元素形成虚树的一颗树链.

当我们得到一些询问点(关键点)的时候,对这些点按照他们的 dfn[u] d f n [ u ] 值进行排序,然后从 dfn d f n 值小的开始扫描,结合栈中保存的树链信息就可以将这颗虚树构建出来.

假设我们当前扫到的关键点为 u u ,栈指针为 top t o p ,栈为 stk s t k .

1.如果栈为空,或者栈中只有一个元素,那么显然应该:
stk[++top]=u; s t k [ + + t o p ] = u ;

2.取 lca=LCA(u,stk[top]) l c a = L C A ( u , s t k [ t o p ] ) ,如果 lca=stk[top] l c a = s t k [ t o p ] ,则说明 u u 点应该接着 stk[top] s t k [ t o p ] 点延长当前的树链.做操作:
stk[++top]=u; s t k [ + + t o p ] = u ;

3.如果 lca≠stk[top] l c a ≠ s t k [ t o p ] ,则说明 u u 与 stk[top] s t k [ t o p ] 分属 lca l c a 的两颗不同的子树,且包含 stk[top] s t k [ t o p ] 的这颗子树应该已经构建完成了,我们需要做的是:
将 lca l c a 的包含 stk[top] s t k [ t o p ] 子树的那部分退栈,并将这部分建边形成虚树.如果 lca l c a 不在栈(树链)中,那么要把 lca l c a 也加入栈中,保证虚树的结构不出现问题,随后将 u u 加入栈中,以表延长树链.

代码实现

//实现逐个将关键点插入形成一颗虚树
void insert(int u){
    if(top <= 1) {stk[++top] = u;return ;}
    int lca = LCA(u,stk[top]);
    if(lca == stk[top]) {stk[++top] = u;return ;}
    while(top > 1 && dfn[lca] <= stk[top-1]) {
        addedge(stk[top-1],stk[top]);
        --top;
    }
    if(lca != stk[top]) stk[++top] = lca;
    stk[++top] = u;
}

虚树例题

[SDOI2011]消耗战

题意

给出 n n 个点的一棵带有边权的树,以及 q q 个询问.每次询问给出 k k 个点,询问这使得这 k k 个点与 1 1 点不连通所需切断的边的边权和最小是多少.

题解

令 dp[n] d p [ n ] 表示从 n n 开始不能到达其子树中的关键点所需切断的最小边权和.

令 me[u] m e [ u ] 表示切断 1 1 到 u u 的路径中的边权最小值.

设 v v 是 u u 的直接儿子.

如果 v v 是关键节点,那么 dp[u]+=me[v][1] d p [ u ] + = m e [ v ] [ 1 ] ,否则 dp[u]+=min(me[v],dp[v])[2] d p [ u ] + = m i n ( m e [ v ] , d p [ v ] ) [ 2 ]
(第 [2] [ 2 ] 个转移方程的解释:要么直接切断 1−v 1 − v 的路径,要么使得从 v v 出发不能到达其子树的关键点.)

显然我们不能针对每个询问对整颗子树进行 dp d p ,时间复杂度过高,而我们发现那些非关键点我们没有必要在 dp d p 的时候考虑,所以使用虚树.

代码

const int maxn = 250007;
const int inf = 1e9;
vector<int> RG[maxn],VG[maxn];
int U[maxn],V[maxn],C[maxn];
int dfn[maxn],deep[maxn];ll me[maxn];int fa[maxn][20];
int stk[maxn],top;
int n,m,idx;
void dfs(int u){
    dfn[u] = ++idx;
    deep[u] = deep[fa[u][0]] + 1;
    for(int e : RG[u]){
        int v = U[e] ^ V[e] ^ u;
        if(v == fa[u][0]) continue;
        me[v] = C[e];
        if(u != 1 && me[u] < me[v]) me[v] = me[u];
        fa[v][0] = u;
        dfs(v);
    }
}

int LCA(int u,int v){
    if(deep[u] < deep[v]) swap(u,v);
    int delta = deep[u] - deep[v];
    for(int i = 19;i >= 0;--i){
        if((delta >> i) & 1) u = fa[u][i];
    }
    for(int i = 19;i >= 0;--i){
        if(fa[u][i] != fa[v][i]) u = fa[u][i],v = fa[v][i];
    }
    if(u == v) return u;
    return fa[u][0];
}

bool comp(int a,int b){
    return dfn[a] < dfn[b];
}

void insert(int u){
    if(top == 1) {stk[++top] = u;return;}
    int lca = LCA(u,stk[top]);
    if(lca == stk[top]) {stk[++top] = u;return ;}
    while(top > 1 && dfn[lca] <= dfn[stk[top-1]]){
        VG[stk[top-1]].push_back(stk[top]);
        --top;
    }
    if(lca != stk[top]) {
        VG[lca].push_back(stk[top]);
        stk[top] = lca;
    } 
    stk[++top] = u;
}

int idq[maxn],mark[maxn];

ll DP(int u){
    ll cost = 0;
    for(int v : VG[u]){
        cost += min(me[v],DP(v));
    }

    VG[u].clear();
    if(mark[u]) return me[u];
    else return cost;
}

int main(){
    init();
    ios::sync_with_stdio(false);
    cin >> n;
    for(int i = 1;i < n;++i){
        cin >> U[i] >> V[i] >> C[i];
        RG[U[i]].push_back(i);
        RG[V[i]].push_back(i);
    }
    dfs(1);
    for(int t = 1;t <= 19;++t) for(int i = 1;i <= n;++i){
        fa[i][t] = fa[fa[i][t-1]][t-1];
    }
    cin >> m;
    for(int i = 0;i < m;++i){
        int sz;
        cin >> sz;
        for(int j = 0;j < sz;++j){
            cin >> idq[j];
            mark[idq[j]] = 1;
        }
        sort(idq,idq+sz,comp);
        top = 0;
        stk[++top] = 1;
        for(int j = 0;j < sz;++j) insert(idq[j]);
        while(top > 0) {
            VG[stk[top-1]].push_back(stk[top]);
            top--;
        }
        cout << DP(1) << endl;
        for(int j = 0;j < sz;++j) VG[idq[j]].clear(),mark[idq[j]] = 0;
        VG[0].clear();
    }
    return 0;
}