强对偶定理的证明

强对偶性的证明

本博客是参考资料的笔记整理：
https://www.bilibili.com/video/BV1dJ411B7gh?p=11

1. 预备知识

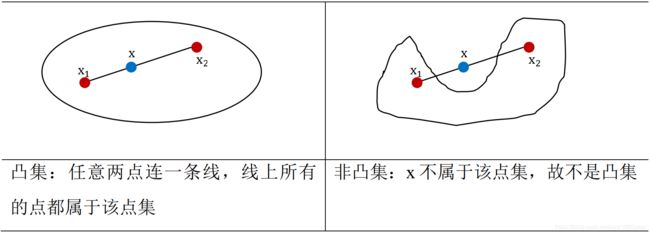
定义 1 凸集：某点集D是凸集，是指对于任意两点$x_1$, $x_2\in D$ 和$0\le \lambda \le 1$，有：
$$x=\lambda x_1+(1-\lambda )x_2\in D\text{\hspace{1em}(1)}$$
以下是凸集的例子

定理 1 分离超平面定理：假设两个不相交的凸集 $C$ 和 $D$，即$C\cap D=\varnothing$，则存在
向量$a\ne 0$和常数$b$，有
$$\{\begin{array}{ll}{\mathbf{a}}^{\mathrm{T}}x\le b& \forall x\in C\\ {\mathbf{a}}^{\mathrm{T}}x\ge b& \forall x\in D\end{array}\text{\hspace{1em}(2)}$$

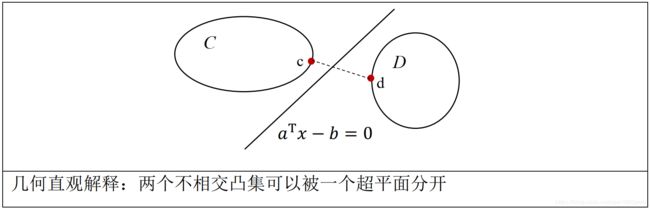
Proof of 定理1:

定义 2：点集的 $C$ 和 $D$ 的之间的距离为：
$$\mathrm{dist}(C,D)=\underset{u\in C,v\in D}{\inf }\Vert u-v{\Vert }^2\text{\hspace{1em}(3)}$$
​ 假设$c\in C,d\in D$能达到此最小距离，即$\mathrm{dist}(C,D)=\Vert c-d{\Vert }^2$，令$a=c-d$，$b=\frac{\Vert c{\Vert }^2-\Vert d{\Vert }^2}{2}$（实际上，$(c-d{)}^{\mathrm{T}}x-\frac{\Vert c{\Vert }^2-\Vert d{\Vert }^2}{2}=0$是点 $c$ 和点 $d$ 连线的“中垂面”），下面证明：①对于任意$u\in C$，有$a^{\mathrm{T}}u-b\ge 0$; ②对于任意$v\in D$，有$a^{\mathrm{T}}v-b\le 0$.

反证法：假设存在一个$u\in C$，使
$$\begin{array}{l}{a}^{\mathrm{T}}u-b<0\\ (c-d{)}^{\mathrm{T}}u-\frac{\Vert c{\Vert }^2-\Vert d{\Vert }^2}{2}<0\\ (c-d{)}^{\mathrm{T}}\left(u-\frac{1}{2}(c+d)\right)<0\\ (c-d{)}^{\mathrm{T}}\left((u-c)+\frac{1}{2}(c-d)\right)<0\\ (c-d{)}^{\mathrm{T}}(u-c)+\frac{1}{2}\Vert c-d{\Vert }^2<0\end{array}$$
因为$-\frac{1}{2}\Vert c-d{\Vert }^2\ge 0$，所以$(c-d{)}^{\mathrm{T}}(u-c)<0$。假设另有一点$p$在 $u$和$c$的连线上，即$p=\lambda u+(1-\lambda )c$，其中 $0\le \lambda \le 1$。根据 $C$ 是凸集，则有$p\in C$。下面计算$\Vert p-d{\Vert }^2$ ：
$$\begin{array}{rl}\Vert p-d{\Vert }^2& =\Vert \lambda u+(1-\lambda )c-d{\Vert }^2\\ & =\Vert (c-d)+\lambda (u-c){\Vert }^2\\ & =\Vert c-d{\Vert }^2+2\lambda (c-d{)}^{\mathrm{T}}(u-c)+{\lambda }^2\Vert u-c{\Vert }^2\\ & =\Vert c-d{\Vert }^2+\lambda \left[2(c-d{)}^{\mathrm{T}}(u-c)+\lambda \Vert u-c{\Vert }^2\right]\end{array}$$
分析$(c-d{)}^{\mathrm{T}}(u-c)<0$，当 $\lambda$ 取一个很小的正数时，即满足
$$\lambda <-\frac{2(c-d{)}^{\mathrm{T}}(u-c)}{\Vert u-c{\Vert }^2}\text{\hspace{1em}(4)}$$
一定有：$\Vert p-d{\Vert }^2<\Vert c-d{\Vert }^2$且$p\in C$，这与定义 2 矛盾，故①得证。而②的证明过程，同理。$■$

定理2：若 $c$ 是一个非零向量，即$\Vert c{\Vert }^2>0$，即则对任意 $\epsilon >0$，存在一个向量 $x$ 满足： ①$\Vert x{\Vert }^2\le \epsilon$ ；②$c^{T}x>0$.

Proof of 定理2: 取$x=\frac{\epsilon }{\Vert c{\Vert }^2}c$，则$\Vert x{\Vert }^2=\epsilon$，且$c^{T}x=\epsilon >0$，同理也存在一个向量 $x$，使①$\Vert x{\Vert }^2\le \epsilon$，②$c^{T}x>0$. $■$

2. 对偶问题

原问题（Prime Problem）：
$$\begin{array}{rl}& \underset{w}{\min }f(w)\\ \text{ s.t. }& g_i(w)\le 0,i=1,2,\dots ,K\\ & h_j(w)=0,j=1,2,\dots ,M\end{array}\text{\hspace{1em}(5)}$$
对偶问题（Dual Problem）：

先定义拉格朗日函数

$$\mathcal{L}(w,\alpha ,\beta )=f(w)+\sum _{i=1}^K{\alpha }_i{g}_i(w)+\sum _{j=1}^M{\beta }_j{h}_j(w)\text{\hspace{1em}(6)}$$
由拉格朗日函数推导出对偶问题的形式：
$$\begin{array}{r}\underset{\alpha ,\beta }{\max }\theta (\alpha ,\beta )=\underset{w}{\inf }\mathcal{L}(w,\alpha ,\beta )\\ \text{ s.t. }{\alpha }_i\ge 0,i=1,2,\dots K\end{array}\text{\hspace{1em}(7)}$$
定理3：若$W^{\ast }$是原问题的解，$\left({\alpha }^{\ast },{\beta }^{\ast }\right)$是对偶问题的解，则有：
KaTeX parse error: Can't use function '$' in math mode at position 2: $̲\theta\left(\al…
Proof of 定理3:
$$\begin{array}{rl}\theta \left({\alpha }^{\ast },{\beta }^{\ast }\right)& =\underset{w}{\inf }\mathcal{L}\left(w,{\alpha }^{\ast },{\beta }^{\ast }\right)\\ & \le \mathcal{L}\left(w^{\ast },{\alpha }^{\ast },{\beta }^{\ast }\right)\\ & =f\left(w^{\ast }\right)+\sum _{i=1}^K{\alpha }_i^{\ast }{g}_i\left(w^{\ast }\right)+\sum _{j=1}^M{\beta }_j^{\ast }{h}_j\left(w^{\ast }\right)\\ & \le f\left(w^{\ast }\right)\end{array}$$
$■$

定义3（凸函数）：$f(w)$是凸函数是指对 $\forall w_1,w_2,\forall \lambda \in [0,1]$，有：
$$f\left(\lambda w_1+(1-\lambda )w_2\right)\le \lambda f\left(w_1\right)+(1-\lambda )f\left(w_2\right)\text{\hspace{1em}(9)}$$

3. 强对偶性的证明

定理4（强对偶定理）：对于$f(w),g_i(w),h_j(w)$，若满足：

①$f(w)$是凸函数；

②$g_i(w)$是凸函数；

③$h_j(w)$是仿射函数，即$h_j(w)=c_j^{\mathrm{T}}w+d$；

④slater条件：存在一个$w$使$g_i(w)<0$和$h_j(w)=0$；

⑤$w$的取值范围$D$是开集，即若 $w\in D$ 则存在邻域$N(w,\epsilon )\in D$；

⑥$w$的取值范围$D$是凸集。

则有：$f\left(w^{\ast }\right)=\theta \left({\alpha }^{\ast },{\beta }^{\ast }\right)$.

Proof of 强对偶定理：

构造点集：
$$A=\left\{(u,v,t)|\exists w\in D,\text{ 使 }{g}_i(w)\le u_i,h_j(w)=v_i,f(w)\le t\right\}\text{\hspace{1em}(10)}$$
定义：
$$g(w)=\left[\begin{array}{c}{g}_1(w)\\ g_2(w)\\ ⋮\\ g_K(w)\end{array}\right],h(w)=\left[\begin{array}{c}{h}_1(w)\\ h_2(w)\\ ⋮\\ h_M(w)\end{array}\right]\text{\hspace{1em}(11)}$$
注意：①若$w\in D$，则$(g(w),h(w),f(w))\in A$（证明：至少可以使定义中等号成立）；②若$w\in D$，则$(+\infty ,h(w),+\infty )\in A$（证明：任何数都小于正无穷）。

引理1：若 $D$ 是凸集，$g_i(w)$是凸函数$(i=1,2,\dots ,K)$，$h_j(w)$是仿射函数，即$h_i(w)=cw+d$，$f(w)$是凸函数，则 $A$ 是凸集.

证明：

设$\left(u_1,v_1,t_1\right),\left(u_2,v_2,t_2\right)\in A$，我们要证当$0\le \lambda \le 1$时，有
$$\left(\lambda u_1+(1-\lambda )u_2,\lambda v_1+(1-\lambda )v_2,\lambda t_1+(1-\lambda )t_2\right)\in A\text{\hspace{1em}(12)}$$
①因为$\left(u_1,v_1,t_1\right)\in A$，所以$\exists w_1\in D$，使$g_i\left(w_1\right)\le u_i,h_j\left(w_1\right)=v_i,f\left(w_1\right)\le t$；同理$\left(u_2,v_2,t_2\right)\in A$，所以 $\exists w_2\in D$，使$g_i\left(w_2\right)\le u_i,h_j\left(w_2\right)=v_i,f\left(w_2\right)\le t$.

②设$w^{\prime }=\lambda w_1+(1-\lambda )w_2$，因为$D$是凸集，所以$w^{\prime }\in D$。由于$g_i(w)$是凸函数，故：$g_i\left(w^{\prime }\right)\le \lambda g_i\left(w_1\right)+(1-\lambda )g_i\left(w_2\right)\le \lambda u_{1,i}+(1-\lambda )u_{2,i}$，同理有$f\left(w^{\prime }\right)\le \lambda t_1+(1-\lambda )t_2$.

③$h_j\left(w^{\prime }\right)=c{w}^{\prime }+d$
$=\lambda \left(c{w}_1+d\right)+(1-\lambda )\left(c{w}_2+d\right)$
$=\lambda h_j\left(w_1\right)+(1-\lambda )h_j\left(w_2\right)$
$=\lambda v_{1,j}+(1-\lambda )v_{2,j}$

综上①②③，引理1得证. $■$

根据式子(10)的定义，我们有原问题的解
$$f\left(w^{\ast }\right)=\underset{(0,0,t)\in A}{\min }t\text{\hspace{1em}(13)}$$
定义另一个点集$B=\left\{(0,0,s)|s<f\left(w^{\ast }\right)\right\}$，可以证明 $B$ 也是凸集，且$A\cap B=\varnothing$.

根据定理1(分离超平面定理)，存在$(\alpha ,\beta ,\eta )$使得：①若$(u,v,t)\in A$，则${\alpha }^{\mathrm{T}}u+{\beta }^{\mathrm{T}}v+\eta t\ge b$；②若$(u,v,t)\in B$，则${\alpha }^{\mathrm{T}}u+{\beta }^{\mathrm{T}}v+\eta t<b$。由于此时，$u=0$和$v=0$，所以$-\eta t<b$.

引理2：若对$\forall (u,v,t)\in A$，有${\alpha }^{\mathrm{T}}u+{\beta }^{\mathrm{T}}v+\eta t\ge b$，则有
$$\alpha =\left[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_K\right]\succcurlyeq 0,\eta \ge 0\text{\hspace{1em}(14)}$$
Proof：

假设某个${\alpha }_i<0$，则可以取相应$u_i=+\infty$，此时$(u,v,t)$仍然属于$A$，但${\alpha }^{\mathrm{T}}u+{\beta }^{\mathrm{T}}v+\eta t=-\infty$，这与${\alpha }^{\mathrm{T}}u+{\beta }^{\mathrm{T}}v+\eta t\ge 0$矛盾。同理可证$\eta \ge 0$。

根据 $A$ 的定义和①可得，对$\forall w\in D$，有${\sum }_{i=1}^K{\alpha }_i{g}_i(w)+{\sum }_{j=1}^M{\beta }_j{h}_j(w)+\eta f(w)\ge b$；根据 $B$ 的定义和②的$-\eta t<b$可得，$\eta f\left(w^{\ast }\right)\le b$。因此有：
$$\sum _{i=1}^K{\alpha }_i{g}_i(w)+\sum _{j=1}^M{\beta }_j{h}_j(w)+\eta f(w)\ge b\ge \eta f\left(w^{\ast }\right)\text{\hspace{1em}(15)}$$
下面分两种情况讨论：

情况1：$\eta \ne 0$，此时有
$$f\left(w^{\ast }\right)\le \sum _{i=1}^K\frac{{\alpha }_i}{\eta }{g}_i(w)+\sum _{j=1}^M\frac{{\beta }_j}{\eta }{h}_j(w)+f(w)=\mathcal{L}\left(w,\frac{\alpha }{\eta },\frac{\beta }{\eta }\right)\text{\hspace{1em}(16)}$$
由于$w$是任意的，因此有
$$f\left(w^{\ast }\right)\le \underset{w}{\inf }\mathcal{L}\left(w,\frac{\alpha }{\eta },\frac{\beta }{\eta }\right)=\theta \left(\frac{\alpha }{\eta },\frac{\beta }{\eta }\right)\text{\hspace{1em}(17)}$$
由于$\alpha \succ 0,\eta >0$，所以$\frac{\alpha }{\eta }\succ 0$，满足对偶问题的限制条件，因此有：
$$f\left(w^{\ast }\right)\le \theta \left({\alpha }^{\ast },{\beta }^{\ast }\right)\text{\hspace{1em}(18)}$$
在根据定理3，有$\theta \left({\alpha }^{\ast },{\beta }^{\ast }\right)\le f\left(w^{\ast }\right)$，所以$f\left(w^{\ast }\right)=\theta \left({\alpha }^{\ast },{\beta }^{\ast }\right)$，得证。

情况2：$\eta =0$，此时对$\forall w\in D$，有
$$\sum _{i=1}^K{\alpha }_i{g}_i(w)+\sum _{j=1}^M{\beta }_j{h}_j(w)\ge 0\text{\hspace{1em}(19)}$$
根据定理4中的条件④（slater条件），$\exists w$使$g_i(w)<0$，$h_j(w)=0$，这可以推出${\alpha }_i=0$，因此公式(19)变为
$$\sum _{j=1}^M{\beta }_j{h}_j(w)\ge 0,\text{ 或记为 }{\beta }^{\mathrm{T}}h(w)\ge 0\text{\hspace{1em}(20)}$$
根据定理4中的条件③，$h(w)=cw+d$，代入得：
$$\begin{array}{l}{\beta }^{\mathrm{T}}h(w)\ge 0\\ {\beta }^{\mathrm{T}}cw+{\beta }^{\mathrm{T}}d\ge 0\end{array}\text{\hspace{1em}(21)}$$
记$P={\beta }^{\mathrm{T}}c$，$q={\beta }^{\mathrm{T}}d$，则式子(21)改写为：
$$Pw+q\ge 0\text{\hspace{1em}(22)}$$
注意公式(22)对所有的$w\in D$都成立。根据条件④ （slater条件），$\exists w$ 使 $cw+d=0$，从而$Pw+q=0$.

下面证明，存在一个 $w^{\prime }=w+\Delta w$，其中$\Delta w$在$w$的一个领域$N(0,\epsilon )$中，使$P{w}^{\prime }+q<0$。

证明：根据定理1，有$\beta \ne 0$，否则$(\alpha ,\beta ,\eta )$都为0，与分离超平面定理矛盾。则有$P={\beta }^{\mathrm{T}}c\ne 0$；根据定理2，存在一个$\Delta w$满足$\Vert w{\Vert }^2<\epsilon$且$P\Delta w<0$。因此，$w^{\prime }=w+\Delta w\in N(0,\epsilon )$。

根据定理4中的条件⑤，$w^{\prime }\in D$，同时，
$$\begin{array}{rl}P{w}^{\prime }+q& =P(w+\Delta w)+q\\ & =(Pw+q)+P\Delta w\\ & =P\Delta w<0\end{array}\text{\hspace{1em}(23)}$$
这与式子(22)矛盾，所以情况2不成立/不存在。

定理4 强对偶定理得证. $■$