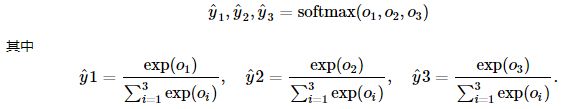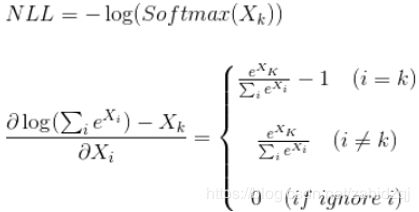动手学深度学习PyTorch版-task1

课程介绍（引用自伯禹平台：https://www.boyuai.com/elites/course/cZu18YmweLv10OeV）

本课程面向希望更多的通过代码实践去学习深度学习原理的同学和在职人士。

《动手学深度学习》是2019年国内最受欢迎的人工智能学习教材之一，伯禹教育携手上海交通大学团队，以此书的知识架构为基础，沿用了其中的原理讲解文档，并将代码框架由MXNET迁移至PyTorch，还对这些优质的实践代码制作了讲解视频。其中部分PyTorch代码来自GitHub开源仓库：https://github.com/ShusenTang/Dive-into-DL-PyTorch。

通过这门课程的学习，你将可以对深度学习中常见的方法以及相关的应用有一个从原理到实践的全面了解。

本课程主要针对代码进行讲解，理论基础较为薄弱的同学，建议配合《动手学深度学习》书籍或本平台上《机器学习》相关知识点学习。

《动手学深度学习》官方网址：http://zh.gluon.ai/ ——面向中文读者的能运行、可讨论的深度学习教科书。

目录：

task1：本章节

task2：https://blog.csdn.net/zahidzqj/article/details/104309590

task3：https://blog.csdn.net/zahidzqj/article/details/104319328

task4：https://blog.csdn.net/zahidzqj/article/details/104324196

task5：https://blog.csdn.net/zahidzqj/article/details/104324349

task5：https://blog.csdn.net/zahidzqj/article/details/104324349

task6：https://blog.csdn.net/zahidzqj/article/details/104451810

task8：https://blog.csdn.net/zahidzqj/article/details/104452274

task9：https://blog.csdn.net/zahidzqj/article/details/104452480

task10：https://blog.csdn.net/zahidzqj/article/details/104478668

1.线性回归

基本概念：模型、数据集、损失函数、优化器、

线性模型：以房价为例，假设价格只取决于房屋状况的两个因素，即面积（平方米）和房龄（年）。接下来我们希望探索价格与这两个因素的具体关系。线性回归假设输出与各个输入之间是线性关系:

price=w1⋅area+w2⋅age+b

数据集：一系列数据包含真实售出价格和它们对应的面积和房龄，通常将数据分为训练集和测试集，面积和房龄两个因素作为特征，真实价格为标签。使用训练集寻找模型参数进行价格预测。

损失函数：在模型训练中，我们需要衡量价格预测值与真实值之间的误差，一般为非负数，可以使用差值得绝对值和平方值。在训练集上计算每一组误差，然后求和。

优化器：梯度下降（求导）

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数 的最小值。梯度下降的每一步中，我们都用到了所有的训练样本，在梯度下降中，在计算微分求导项时，我们需要进行求和运算，所以，在每一个单独的梯度下降中，我们最终都要计算这样一个东西，这个项需要对所有个训练样本求和。因此，批量梯度下降法这个名字说明了我们需要考虑所有这一"批"训练样本，而事实上，有时也有其他类型的梯度下降法，不是这种"批量"型的，不考虑整个的训练集，而是每次只关注训练集中的一些小的子集。

代码示例：伯禹平台的代码是使用jupyter，并使用两种写法

从零开始的实现（推荐用来学习）：能够更好的理解模型和神经网络底层的原理

使用pytorch的简洁实现：能够更加快速地完成模型的设计与实现

以下代码是借鉴伯禹的pytorch写法，改为py文件，可以直接运行。

import torch
from torch import nn
import numpy as np
torch.manual_seed(1)

#generate data
num_inputs = 2
num_examples = 1000

true_w = [2, -3.4]
true_b = 4.2

features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)

#load data
import torch.utils.data as Data

batch_size = 10

# combine featues and labels of dataset
dataset = Data.TensorDataset(features, labels)

# put dataset into DataLoader
data_iter = Data.DataLoader(
    dataset=dataset,            # torch TensorDataset format
    batch_size=batch_size,      # mini batch size
    shuffle=True,               # whether shuffle the data or not
    num_workers=0,              # read data in multithreading
)

#define module
class LinearNet(nn.Module):
    def __init__(self, n_feature):
        super(LinearNet, self).__init__()      # call father function to init 
        self.linear = nn.Linear(n_feature, 1)  # function prototype: `torch.nn.Linear(in_features, out_features, bias=True)`

    def forward(self, x):
        y = self.linear(x)
        return y
#load net  
net = LinearNet(num_inputs)
print(net)

#define loss
loss = nn.MSELoss()

#define optimizer
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03)   # built-in random gradient descent function
#train
num_epochs = 3
for epoch in range(1, num_epochs + 1):
    for X, y in data_iter:
        output = net(X)
        l = loss(output, y.view(-1, 1))
        optimizer.zero_grad() # reset gradient, equal to net.zero_grad()
        l.backward()
        optimizer.step()
    print('epoch %d, loss: %f' % (epoch, l.item()))

#view para
for param in net.parameters():
    print(param)

2.softmax和分类模型

基本概念：softmax、交叉熵、Fashion-MNIST数据集、数据读取

softmax运算：将输出值变换成值为正且和为1的概率分布

同时满足

因此softmax运算不改变预测类别输出。

softmax求导：

先取负对数损失：

交叉熵：比较复杂，难以理解，附上讲的比较清晰的链接:https://www.cnblogs.com/kyrieng/p/8694705.html

softmax和交叉熵的连用：

torchvision包是服务于PyTorch深度学习框架的，主要用来构建计算机视觉模型。torchvision主要由以下几部分构成：

1. torchvision.datasets: 一些加载数据的函数及常用的数据集接口；
2. torchvision.models: 包含常用的模型结构（含预训练模型），例如AlexNet、VGG、ResNet等；
3. torchvision.transforms: 常用的图片变换，例如裁剪、旋转等；
4. torchvision.utils: 其他的一些有用的方法。

数据加载：

mnist_train = torchvision.datasets.FashionMNIST(root='/home/kesci/input/FashionMNIST2065', train=True, download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='/home/kesci/input/FashionMNIST2065', train=False, download=True, transform=transforms.ToTensor())

• root（string）– 数据集的根目录，其中存放processed/training.pt和processed/test.pt文件。
• train（bool, 可选）– 如果设置为True，从training.pt创建数据集，否则从test.pt创建。
• download（bool, 可选）– 如果设置为True，从互联网下载数据并放到root文件夹下。如果root目录下已经存在数据，不会再次下载。
• transform（可被调用 , 可选）– 一种函数或变换，输入PIL图片，返回变换之后的数据。如：transforms.RandomCrop。
• target_transform（可被调用 , 可选）– 一种函数或变换，输入目标，进行变换。

3.多层感知机

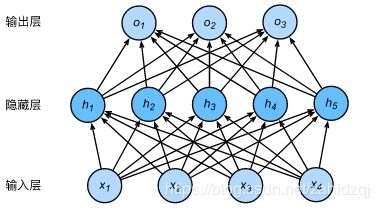
基本概念：隐藏层、前向传播、激活函数

隐藏层：上图展示了一个多层感知机的神经网络图，它含有一个隐藏层，该层中有5个隐藏单元。

前向传播表达式：X作为输入，H代表隐藏层，O代表输入，那么可以表示为：

 也就是将隐藏层的输出直接作为输出层的输入。如果将以上两个式子联立起来，可以得到：

从联立后的式子可以看出，虽然神经网络引入了隐藏层，却依然等价于一个单层神经网络：其中输出层权重参数为WhWo，偏差参数为bhWo+bo。即便再添加更多的隐藏层，以上设计依然只能与仅含输出层的单层神经网络等价。

激活函数：述问题的根源在于全连接层只是对数据做仿射变换（affine transformation），而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，本质上就是激活函数加入了非线性因素，弥补了线性模型的表达力，把“激活的神经元的特征”通过函数保留并映射到下一层。因为神经网络的数学基础是处处可微的，所以选取的激活函数要能保证数据输入与输出也是可微的。

ReLU函数是目前最常见的激活函数，应用范围很广，现在大部分的卷积神经网络都采用 relu 作为激活函数，其比例大概达到80%以上。

对应的数学表达公式为：

常见的激活函数包括平滑非线性的激活函数，如 sigmoid、tanh、softplus 和 softsign，也包括连续但不是处处可微的 函数 relu、relu6 和 relu_x，以及随机正则化函数 dropout。

关于激活函数的选择

ReLu函数是一个通用的激活函数，目前在大多数情况下使用。但是，ReLU函数只能在隐藏层中使用。

sigmoid函数还可以做二分类使用。在神经网络层数较多的时候，最好使用ReLu函数，ReLu函数比较简单计算量少，而sigmoid和tanh函数计算量大很多（求导复杂，影响时间）。

还可以根据实际尝试不同的激活函数。

问题：

relu函数在左半轴都为0，不会梯度消失吗？

见解：所以relu函数  有降低数据维度的作用吧。在左半轴丢失的信息，可能不影响整个特征的传递，反倒有助于网络性能吧