# coding: utf-8
# 利用 diabetes数据集来学习线性回归
# diabetes 是一个关于糖尿病的数据集, 该数据集包括442个病人的生理数据及一年以后的病情发展情况。
# 数据集中的特征值总共10项, 如下:
# 年龄
# 性别
#体质指数
#血压
#s1,s2,s3,s4,s4,s6 (六种血清的化验数据)
#但请注意,以上的数据是经过特殊处理, 10个数据中的每个都做了均值中心化处理,然后又用标准差乘以个体数量调整了数值范围。验证就会发现任何一列的所有数值平方和为1.
#关于数据集更多的信息: http://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_diabetes.html
# http://scikit-learn.org/stable/datasets/index.html#datasets
import numpy as np
from sklearn import datasets
diabetes=datasets.load_diabetes()
#查看第一列年龄的数据
diabetes.data[0]
#求证: 每一列的数值的平方和为1
np.sum( diabetes.data[:,0]**2) #求年龄列
#糖尿病进展的数据
diabetes.target #数值介于 25到346之间
#切分训练集与测试集
#自动切分训练集太小了
#from sklearn.cross_validation import train_test_split
#x_train,x_test,y_train,y_test=train_test_split( diabetes.data,diabetes.target,random_state=14)
#所以换成手工切分
x_train=diabetes.data[:-20]
y_train=diabetes.target[:-20]
x_test=diabetes.data[-20:]
y_test=diabetes.target[-20:]
#什么是回归呢? 回归的目的是预测数值型的目标值。最直接的办法是根据训练数据计算出一个求目标值的计算公式。假如你想预测一个地区的餐馆数量,可能会这么计算:
# num = 0.002 * people + 0.001 * gpd
# 以上就是所谓的回归方程,其中的0.002, 0.001称作回归系数,求这些回归系数的过程就是回归。一旦求出了这些回归系数,再给定输入,做预测就简单了.
# 回归分为线性回归和非线性回归。 上面的公式描述的就是线性回归.
#线性回归通过拟合线性模型的回归系数W =(w_1,…,w_p)来减少数据中观察到的结果和实际结果之间的残差平方和,并通过线性逼近进行预测。
#scikit-learn库的线性回归预测模型通过fit(x,y)方法来训xaisaj型,其中x为数据的属性,y为所属的类型.线性模型的回归系数W会保存在它的coef_方法中.
from sklearn import linear_model
linreg=linear_model.LinearRegression() #创建线性回归
#用训练集训练模型
linreg.fit( x_train,y_train)
#调用预测模型的coef_属性,求出每种生理数据的回归系数b, 一共10个结果,分别对应10个生理特征.
linreg.coef_
#在模型上调用predict()函数,传入测试集,得到预测值,
linreg.predict( x_test )
#结果:array([ 197.61846908, 155.43979328, 172.88665147, 111.53537279,
# 164.80054784, 131.06954875, 259.12237761, 100.47935157,
# 117.0601052 , 124.30503555, 218.36632793, 61.19831284,
# 132.25046751, 120.3332925 , 52.54458691, 194.03798088,
# 102.57139702, 123.56604987, 211.0346317 , 52.60335674])
#查看实际目标值
y_test
#array([ 233., 91., 111., 152., 120., 67., 310., 94., 183.,
# 66., 173., 72., 49., 64., 48., 178., 104., 132.,
# 220., 57.])
#如何评价以上的模型优劣呢?我们可以引入方差,方差越接近于1,模型越好.
# 方差: 统计中的方差(样本方差)是各个数据分别与其平均数之差的平方的和的平均数
linreg.score( x_test,y_test)
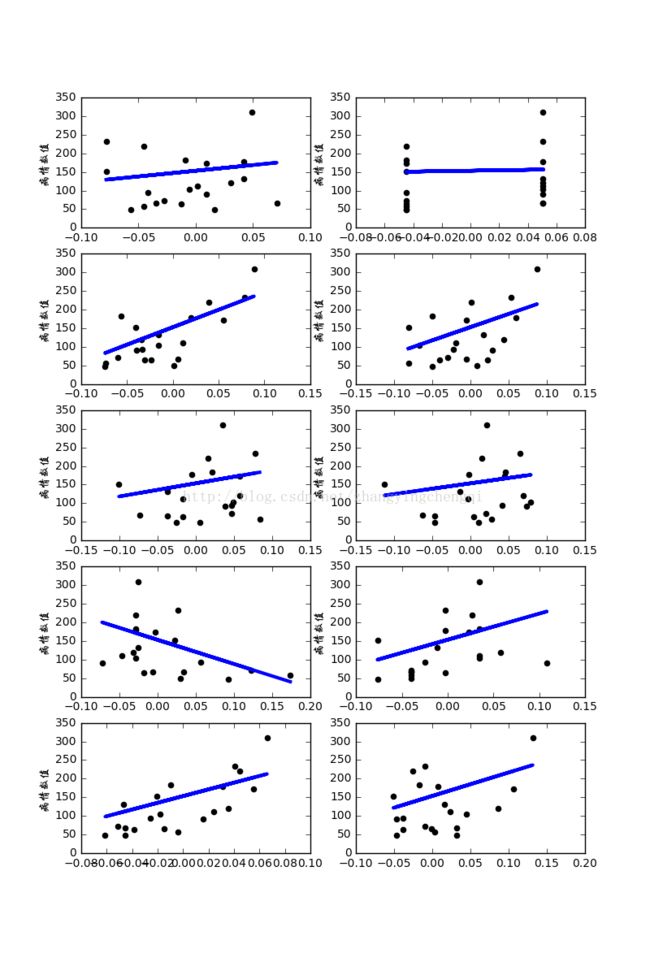
#对每个特征绘制一个线性回归图表
import matplotlib.pyplot as plt
#matplot显示图例中的中文问题 : https://www.zhihu.com/question/25404709/answer/67672003
import matplotlib.font_manager as fm
#mac中的字体问题请看: https://zhidao.baidu.com/question/161361596.html
myfont = fm.FontProperties(fname='/Library/Fonts/Xingkai.ttc')
plt.figure( figsize=(8,12))
#循环10个特征
for f in range(0,10):
#取出测试集中第f特征列的值, 这样取出来的数组变成一维的了,
xi_test=x_test[:,f]
#取出训练集中第f特征列的值
xi_train=x_train[:,f]
#将一维数组转为二维的
xi_test=xi_test[:,np.newaxis]
xi_train=xi_train[:,np.newaxis]
plt.ylabel(u'病情数值',fontproperties=myfont)
linreg.fit( xi_train,y_train) #根据第f特征列进行训练
y=linreg.predict( xi_test ) #根据上面训练的模型进行预测,得到预测结果y
#加入子图
plt.subplot(5,2,f+1) # 5表示10个图分为5行, 2表示每行2个图, f+1表示图的编号,可以使用这个编号控制这个图
#绘制点 代表测试集的数据分布情况
plt.scatter( xi_test,y_test,color='k' )
#绘制线
plt.plot(xi_test,y,color='b',linewidth=3)
plt.savefig('python_糖尿病数据集_预测病情_线性回归_最小平方回归.png')
plt.show()