leetcode题解：第84题Largest Rectangle in Histogram

题目

Largest Rectangle in Histogram

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

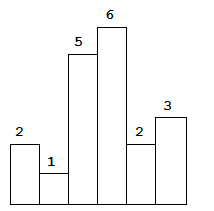
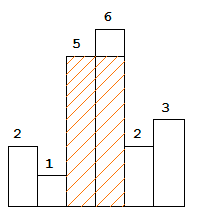
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

Input: [2,1,5,6,2,3]
Output: 10

分析

这道题看起来和之前那道**Trapping Rain Water**很像，给的例题都有直方图，但这题要求的是直方图中能找到的最大矩形面积，要求连续的几个数数值越近越好，就能组成更大的面积，与之前那道正好相反。

解法一

首先，最容易想到的解法就是对数组中的每个高度都求出对应的最大矩形面积，然后取最大值，即为答案。

要求固定高度h的最大矩形面积的话，我们需要遍历整个数组，然后记录每一个能够组成的高度为h的矩形面积，最后取最大值，伪代码如下：

for i in heights do
	if (heights[i] >= h) //这个元素作为当前矩形的一部分
    else //该元素高度小于矩形高度，计算当前矩形面积

需要注意的几点：

• 计算矩形面积后要及时更新矩形的左右下标为初始值
• 当最后一个元素也大于矩形高度时，不能忽略这个矩形的高度
• 为了避免重复计算，可以用map来存储已经计算过的高度对应的面积

代码

class Solution {
public:
    int largestRectangleArea(vector& heights) {
        int result = 0;
        maparea;
        for (auto i : heights) {
            //判断这个高度的矩形的面积是否被计算过
            if (area.find(i) == area.end()) {
                area.insert(std::pair(i, calc(i, heights)));
                result = max(result, area[i]);
            }
        }
        return result;
    }
private:
    int calc(int h, const vector& heights) {
        int left, right;
        left = right = -1;
        int area = 0;
        for (int i = 0; i < heights.size(); ++i) {
            //矩形左下标
            if (heights[i] >= h && left == -1) left = right = i;
            //矩形右下标右移
            else if (heights[i] >= h) right++;
            //h小于矩形高度，计算当前最大矩形面积
            else if (left != -1) {
                area = max(area, (right - left + 1) * h);
                left = right = -1;
            }
        }
        //不要遗漏右下标为最后一个下标的矩形面积
        if (right == heights.size() - 1) {
            area = max(area, (right - left + 1) * h);
        }
        return area;
    }
};

复杂度分析

这种解法在最好情况下复杂度为O(2n)，即数组中所有元素值都相等时；最坏情况下复杂度为O(n²)，即数组中所有元素值都不相等时。

但是这种解法在leetcode上运行时间超过了1000ms，因此必须进行优化。

解法二

上面那种解法在经过了使用map来避免重复计算后运行时间还是很高，这是因为计算每个高度对应的面积时都必须遍历整个数组，我们要从这一点入手来进行优化。

但是每个高度对应的面积之间貌似没有联系，不能通过一个值来推出其他值，因此我考虑换一种基本思路：计算每个包含当前元素的矩形面积，然后取最大值。这个计算要求我们从当前元素下标开始，分别向左和向右找第一个高度小于当前元素的下标，然后就是(right - left - 1) * height，伪代码如下：

for i in heights do
	for j = i - 1 to 0 do
    	if (heights[j] < heights[i]) left = j;break
    for j = i + 1 to 0 do
    	if (heights[j] < heights[i]) right = j;break
    result = max(result, (right - left - 1) * heights[i])

这种基本思路的解法比解法一的复杂度还会稍微高一点，但是重点是它是可以优化的，因为相邻两个元素之间的left值和right值是有联系的：

假设从左往右遍历，如果当前元素高度大于它左边元素高度，那么它的left值就是左边元素的下标；否则，需要往左遍历去寻找left值。但是通过存储每个元素的left值和right值，可以简化这个遍历过程，伪代码如下：

int left[n], right[n];
for i in heights do
	if (heights[i] > heights[i - 1]) left[i] = i - 1
    else {
        int tmp = left[i - 1]
        while (heights[i] <= heights[tmp]) tmp = left[tmp]
        left[i] = tmp
    }

因为元素j高度大于元素i高度，因此第一个高度小于元素i的下标一定<=元素j的left值，通过利用数组，我们可以快速完成遍历，提高算法速度。

最终的算法需要遍历两次数组，分别求解出left和right数组，然后计算面积，可以把计算面积的过程放在求解right数组的循环中来减少运行时间。

代码

class Solution {
public:
    int largestRectangleArea(vector& heights) {
        int result = 0;
        int n = heights.size();
        if (n == 0) return 0;
        int left[n], right[n];
        left[0] = -1;
        right[n - 1] = n;
        for (int i = 1; i < n; ++i) {
            if (heights[i] > heights[i - 1]) left[i] = i - 1;
            else {
                //找第一个小于当前元素的元素下标
                int tmp = left[i - 1];
                while (heights[i] <= heights[tmp] && tmp != -1) {
                    tmp = left[tmp];
                }
                left[i] = tmp;
            }
        }
        for (int i = n - 2; i >= 0; --i) {
            if (heights[i] > heights[i + 1]) right[i] = i + 1;
            else {
                //找第一个小于当前元素的元素下标
                int tmp = right[i + 1];
                while (heights[i] <= heights[tmp] && tmp != n) {
                    tmp = right[tmp];
                }
                right[i] = tmp;
            }
            result = max(result, (right[i] - left[i] - 1) * heights[i]);
        }
        result = max(result, (right[n - 1] - left[n - 1] - 1) * heights[n - 1]);
        return result;
    }
};

复杂度分析

算法的复杂度在最坏情况下为O(n²)，但这种情况很难遇到，更一般的情况下可以逼近O(n)，在leetcode上运行时间为12ms。

解法三

第三种解法是大家熟知的单调栈解法，即用栈存下柱子的高度，栈内高度是递增的，栈顶高度最大。
当遍历所有的高度时，如果当前高度大于栈顶高度，则入栈；否则就出栈并计算这个栈顶高度的面积，当前高度就是其右边第一个小的高度，新的栈顶高度就是其左边第一个小的高度。栈内存放的是高度的索引。

代码

class Solution {
public:
    int largestRectangleArea(vector& heights) {
       int result = 0;
        stack tmp;
        heights.insert(heights.begin(), 0);
        heights.push_back(0);
        for (int i = 0; i < heights.size(); ++i) {
            while (!tmp.empty() && heights[i] < heights[tmp.top()]) {
                int h = heights[tmp.top()];
                tmp.pop();
                result = max(result, (i - tmp.top() - 1) * h);
            }
            tmp.push(i);
        }
        return result;
    }
};

复杂度分析

总结

第一种解法虽然利用map省去了重复计算，但是每一次计算的复杂度还是很高；而第二种解法利用每个矩形左右下标之间的联系，简化了计算的过程，使算法提速明显，因此我们在设计算法时要尽量利用已知来求解未知，简化计算过程。