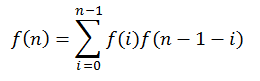由入栈123出栈顺序引发的思考

 

由入栈123出栈顺序引发的思考

 

最近在看数据结构，一道题引起了我的注意。

目录

由入栈123出栈顺序引发的思考    1

1、题    1

2、栈的理解    1

3、由题引发的思考    2

4、用"子问题"的方法寻找n个元素进栈有多少个出栈顺序    2

5、不管三七二十一，java代码搞起来！（先实现了再说）    3

6、小结（贪婪）    5

7、Wiki百科给了答案，写的非常详细http://en.wikipedia.org/wiki/Catalan_number  （自带）    5

8、现在的问题就是：怎么从上述的递推公式求出C(2n,n)/(n+1) ?    8

9、翻阅其他资料，C(2n,n)-C(2n,n-1) 也是符合的    8

10、总结：    8

 

 

1、题

4.     一个栈的输入序列为1 2 3，则下列序列中不可能是栈的输出序列的是( C )

A. 2 3 1                            B. 3 2 1

C. 3 1 2                         D. 1 2 3

 

2、栈的理解

官方----栈（stack）又名堆栈，它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

---《百度百科》

通俗----某大神解释栈就是吃了吐，先吃的先吐，后吃的后吐，（堆就是吃了拉，先吃的先拉，后吃的后拉）

 

再来看这道题

 

3、由题引发的思考

刚开始看到这道题，怎么做?

分析A. 2 3 1     很好分析 1 入栈 2 入栈 2 出栈 3 入栈 3出栈 1 出栈

 

B. 3 2 1 很简单 1 入栈 2 入栈 3 入栈 3出栈 2 出栈 1出栈

C. 3 1 2 impossible 3 第一个出栈，说明1 2 已经入栈了，此时顺序只能是 3 2 1

D. 1 2 3 1 入栈 1 出栈 2 入栈 2 出栈 3入栈 3出栈

 

1、这道题算是解开了，但是不能一个个分析吧，有没有简单的规律，（经尝试，没有像高中老师总结的"奇变偶不变 符号看象限"的简单明了的规律，唯一点值得注意的是：如果让选不正确的答案，可以首先在最后一位是第一个出栈的答案上找 ，就是 进栈 123 ，首先看 3在第一位的答案）

2、但题目变成多选，又该怎么办（能不能找到n个元素入栈有F(n)种出栈顺序的规律）？ 发现1个元素进栈，有1种出栈顺序；2个元素进栈，有2种出栈顺序；3个元素进栈，有5种出栈顺序 那么 4个元素进栈，出栈是不是 15种？（然而真相总是掩藏在事实深处，需要透过现象看本质）

 

4、用"子问题"的方法寻找n个元素进栈有多少个出栈顺序

就是递推

1个元素进栈，有1种出栈顺序； f(1)=1

2个元素进栈，有2种出栈顺序； f(2)=2

3个元素进栈，有5种出栈顺序 f(3)=5

4个元素进栈，有几种呢？

开始算

 我们给4个元素编号为a,b,c,d, 那么考虑：元素a只可能出现在1号位置，2号位置，3号位置和4号位置(很容易理解，一共就4个位置，比如abcd,元素a就在1号位置)。

1) 如果元素a在1号位置，那么只可能a进栈，马上出栈，此时还剩元素b、c、d等待操作，就是子问题f(3)；

2) 如果元素a在2号位置，那么一定有一个元素比a先出栈，即有f(1)种可能顺序（只能是b），还剩c、d，即f(2)，根据乘法原理，一共的顺序个数为f(1) * f(2)；

3) 如果元素a在3号位置，那么一定有两个元素比1先出栈，即有f(2)种可能顺序（只能是b、c），还剩d，即f(1)，

根据乘法原理，一共的顺序个数为f(2) * f(1)；

4) 如果元素a在4号位置，那么一定是a先进栈，最后出栈，那么元素b、c、d的出栈顺序即是此小问题的解，即f(3)；

结合所有情况，即f(4) = f(3) + f(2) * f(1) + f(1) * f(2) + f(3);

规整化我们定义f(0) = 1；于是：

f(4) = f(0)*f(3) + f(1)*f(2) + f(2) * f(1) + f(3)*f(0)=14

f(3)= f(0)*f(2) + f(1)*f(1) + f(2) * f(0)=5

f(2)=f(0)*f(1)+f(1)*f(0)=2

即

f(n) = f(0)*f(n-1) + f(1)*f(n-2) + ... + f(n-1)*f(0)

5、不管三七二十一，java代码搞起来！（先实现了再说）

 

//这种数学公式转化java代码是最好转化的了

publicclass CatalanNumber
{    
    publicstaticvoid main(String[] args)
    {        
        int n = 7;        
        System.out.println(Catalan(n));    
    }    
    publicstaticint Catalan(int n)
    {        
        int result = 0;        
        for(int i = 0; i <= n - 1; i++)
        {            
            result += f(i) * f(n - 1 - i);        
        }        
        return result;    
    }    
    publicstaticint f(int n)
    {        
        if(n == 1 || n == 0)
        {            
            return 1;        
        }        
        if(n == 2)
        {            
            return 2;        
        }        
        if(n == 3)
        {            
            return 5;        
        }        
        if(n == 4)
        {            
            return 14;        
        }        
        returnCatalan(n);    
    }
}

（肯定还有其他的实现代码）

算以至此，我们已经得到了一个想要的答案了，但是，如果给7个数

则

F(7)= f(0)*f(6)+ f(1)*f(5) + f(2)*f(4) + f(3)*f(3) + f(4)*f(2) + f(5)*f(1) + f(6)*f(0)=429

我们现在只能记住 f(1)=1 ; f(2)=2 ;f(3)=5; f(4)=14 f(5)=42

f(6)这里出现了， 又要计算f(6)

f(6)= f(0)*f(5)+ f(1)*f(4) + f(2)*f(3) + f(3)*f(2) + f(4)*f(1) + f(5)*f(0)=132

6、小结（贪婪）

 

但是我们不是计算机，而且这个算法的时间复杂度最起码是在O(n^2)，人类都是处女座，

极尽完美, 贪婪，能不能有时间复杂度是0(1)？

 

7、Wiki百科给了答案，写的非常详细http://en.wikipedia.org/wiki/Catalan_number  （自带）

package shujujiegou;
/**

*

* @author阿亮

*

*/
publicclass CatalanNumber
{    
    publicstaticvoid main(String[] args)
    {        
        int n = 6;        
        System.out.println(Catalan(n));        
        System.out.println(cc1(n));     //时间复杂度为O(1); 新算法
            
    }    
    publicstaticint Catalan(int n)
    {        
        int result = 0;        
        for(int i = 0; i <= n - 1; i++)
        {            
            result += f(i) * f(n - 1 - i);        
        }        
        return result;    
    }    
    publicstaticint f(int n)
    {        
        if(n == 1 || n == 0)
        {            
            return 1;        
        }        
        if(n == 2)
        {            
            return 2;        
        }        
        if(n == 3)
        {            
            return 5;        
        }        
        if(n == 4)
        {            
            return 14;        
        }        
        returnCatalan(n);    
    }    
    publicstaticint cc(int n1, int n2)
    { //时间复杂度为O(1);新算法
                
        int index = 1;        
        int a = 1;        
        int b = 1;        
        for(int i = n1; i > n1 - n2; i--)
        {            
            a *= i;            
            b *= index++;        
        }        
        return a / b;    
    }    
    publicstaticint cc1(int n)
    { //时间复杂度为O(1);新算法
                
        return Math.abs(cc(2 * n, n) / (n + 1));    
    }         
}

结果是C(2n,n)/(n+1)，不多说代码搞起来，在原来类里写了

大量数据表明是正确的，

8、现在的问题就是：怎么从上述的递推公式求出C(2n,n)/(n+1) ?

穷尽脑汁，极尽度日之所学，仍不得解，遂google 知乎 。（也许成立社成老师可以）

 

还是上面维基百科的例子，Wiki给出了5种证明过程。

愚钝，每种都不懂!

 

 

9、翻阅其他资料，C(2n,n)-C(2n,n-1) 也是符合的

 

从几何上推出了"n个元素进栈有多少个出栈顺序"这个问题的答案是C(2n,n)-C(2n,n-1)，但是原答案找不到了

 

 

10、总结：

对于结题

1、如果让选不正确的答案，可以首先在最后一位是第一个出栈的答案上找 ，就是 进栈 123 ，首先看 3在第一位的答案）

2、如过多选C(2n,n)/(n+1) 或者C(2n,n)-C(2n,n-1) 能判断正确的组合有多少种

对于继续深究，可以将维基百科的内容读懂！

 

 

 

部分内容摘自博客

http://blog.csdn.net/me4weizhen/article/details/52614298