算法 之 分治 - 合并排序-自顶向下合并排序
这次讲的算法与自底向上算法(ButtomUpSort)很类似,但是实现起来比它更加简单。
在 ButtomUpSort 算法中,我们已经知道了元素是如何由关联排序树的逐层隐含遍历完成排序的。在每一层中,我们有已排序的序列对,然后将它们合并而得到较大的排序序列。沿着树一层一层向上继续这个过程,直到到达根为止,这最后的序列就是已经排序好的。
如果你不了解 BottomUpSort 算法的基本思想,可以参考:算法 之 分治 - 合并排序-自底向上合并排序。
现在,让我们从反向来考虑,也就是 自顶向下 取代 自底向上。一开始有输入数组 A = { 9, 4, 5, 2, 1, 7, 4, 6 }
将该数组分成两个4元素的数组 { 9, 4, 5, 2 } 和 { 1, 7, 4, 6}
接着分别对这两个数组的元素排序,然后只是将它们合并来得到所希望的排序数组,这称为 Sort。
至于每一半用的排序方法,可以随意使用任何排序算法来对这两个子数组排序,特别是可以使用算法 Sort 本身。
实际上这就是著名的算法 MergeSort 的思想。
过程 MergeSort
输入 n 个元素的数组 A[1...n]
输出 按非降序排列的数组 A[1...n]
算法描述 mergeSort(A, low, high)
if low < high then
mid ← ⌊(low + high) / 2⌋
mergeSort(A, low, middle)
mergeSort(A, middle + 1, high)
Merge(A, low, middle, high)
end if
算法中用到的 Merge 方法,可以参考:算法 之 分治 - 合并排序-合并两个已排序的表
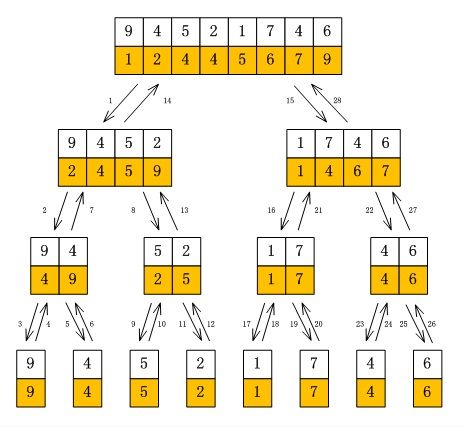
以下图示显示了对数组 A 的操作过程,
与 BottomUpSort 算法一样,MergeSort 算法所执行的元素比较总次数在 (n log n)/2 和 n log n - n + 1之间。
以下是此算法的一种 Java 实现:
public static void mergeSort(int[] array, int low, int high)
{
if (low >= high)
return;
int middle = (low + high) / 2;
mergeSort(array, low, middle);
mergeSort(array, middle + 1, high);
merge(array, low, middle, high);
}