SVM算法（二）线性可分的SVM求解

回忆前文提到的感知机模型：对于线性可分的二分类问题，通过不断迭代错误分类样本点，直至最终的分割面。
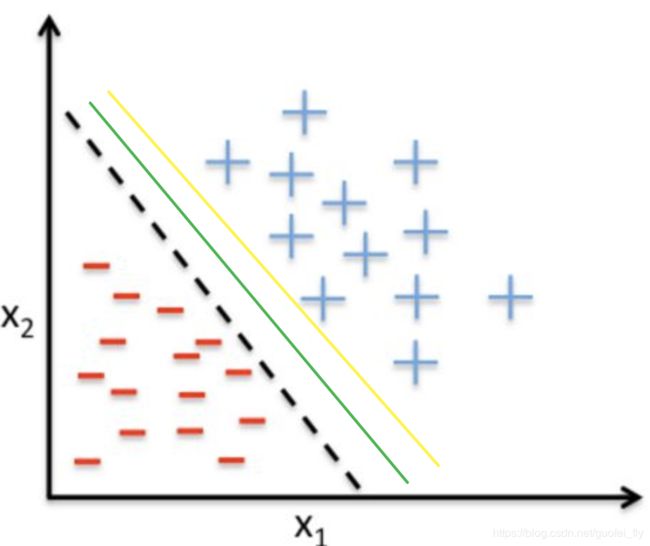
感知机是错误样本驱动的分类器，显然对于线性可分的数据，这样的分类器有无数个（见下图），那究竟哪一个更好呢？
直觉上，在下图给出的三个分割面上，绿色的分割面更佳。因为其离正、负样本更远，这意味着模型更能够忍受数据误差（测量或采样等导致），即模型更健壮。而这就是线性可分的SVM推导的切入点。

一、线性可分最优化问题的引出

设平面方程为$wx+b=0$，任意点$x_i$到平面的距离可写成$\frac{1}{||w||}|w{x}_i+b|$。显然若数据可分，则对于合适的分割面，有$y_i(w{x}_i+b)>0$。注意到$y_i=\{+1,-1\}$，目标问题可表示为：
$$\begin{array}{rl}& \max \gamma \\ & \gamma =\underset{i}{\min }\frac{1}{||w||}{y}_i(w{x}_i+b)\end{array}$$
值的注意的是：对于任意一组$w$、$b$值，任意缩放若干倍，并不影响分隔面本身，也不影响目标问题的解。那我们不妨选择合适的一组$w$、$b$，使得$\underset{i}{\min }{y}_i(w{x}_i+b)=1$。此时$\gamma =\frac{1}{||w||}$，对应的目标问题可改写为：
$$\begin{array}{rl}& \max \frac{1}{||w||}\\ & \underset{i}{\min }{y}_i(w{x}_i+b)=1\end{array}$$将上式中的最小化条件改为不等式约束，可进一步得到优化目标为：
$$\begin{array}{rl}& \max \frac{1}{||w||}\\ & s.t.y_i(w{x}_i+b)\ge 1\end{array}$$需要强调的是，对于不等式约束条件，必然存在若干点$(x_j,y_j)$使得等号成立，即$y_j(w{x}_j+b)=1$，否则可通过缩小$w,b$使得等号成立，从而获得更大的$\max \frac{1}{||w||}$。从几何意义上，这些点就是与分割面距离恰为$\frac{1}{||w^{\ast }||}$的点，也称支持向量点，而$\frac{1}{||w^{\ast }||}$称为间隔(margin)，或几何间距。$\frac{2}{||w^{\ast }||}$为分割面两侧支持点的距离，也是正负分类的最近距离(见下图)。

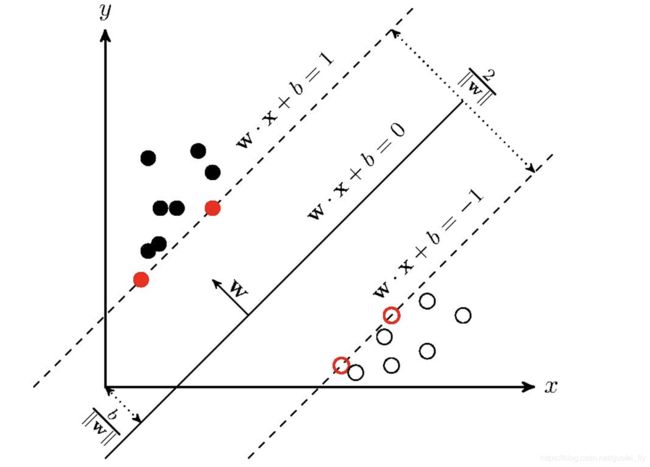
根据最优化理论，我们更习惯于求解最小化问题。因此，此最优化问题可写成：$$\begin{array}{rl}& \min \frac{1}{2}{w}^2\\ & s.t.y_i(w{x}_i+b)\ge 1\end{array}$$
注意到目标函数$\min \frac{1}{2}{w}^2$为凸函数，而约束条件$y_i(w{x}_i+b)\ge 1$为仿射函数。根据二次规划理论，其可求解！

上文在推导过程，$x_i$为原始的输入特征，在实际操作中上可以通过$x_i$的各种函数（非线性变换）得到海量的高维特征（甚至无穷维）。随着特征维度的扩张，使得计算量迅速扩大。
那是否有方法解决这种矛盾呢？下面来就来介绍解决这个问题的对偶算法。

二、SVM的对偶问题

根据优化目标和约束条件，定义广义拉格朗日函数：$$L(w,b,\alpha )=\frac{1}{2}{w}^2+\sum _i{\alpha }_i(1-y_i(w{x}_i+b)),\alpha \ge 0$$对于原始最大最小问题：$$\underset{w,b}{\min }\underset{\alpha }{\max }L(w,b,\alpha )$$如果存在不满足约束条件的$x_i,y_i$，即$y_i(w{x}_i+b)\le 1$，则可令${\alpha }_i\to +\infty$，使得$\underset{\alpha }{\max }L(w,b,\alpha )\to +\infty$
而对于满足约束的$x_i,y_i$，考虑到$y_i(w{x}_i+b)\ge 1$且${\alpha }_i\ge 0$，因此$\underset{\alpha }{\max }L(w,b,\alpha )=\frac{1}{2}{w}^2$。所以原来的带约束的不等式问题，变成了如下的不带约束的拉格朗日最大最小值问题：$$\underset{w,b}{\min }\underset{\alpha }{\max }\frac{1}{2}{w}^2+\sum _i{\alpha }_i(1-y_i(w{x}_i+b)),\alpha \ge 0$$对应的对偶问题，即拉格朗日最小最大值问题可写成：
$$\underset{\alpha }{\max }\underset{w,b}{\min }\frac{1}{2}{w}^2+\sum _i{\alpha }_i(1-y_i(w{x}_i+b)),\alpha \ge 0$$
对于内部的最小化目标函数${\min }_{w,b}L(w,b)$，将$\alpha$作为定值，仅存在$w,b$两个原始变量，可直接根据梯度为0求解最小值对应的点：$$\begin{array}{rl}& {\nabla }_{w}L(w,b)=w-\sum _i{\alpha }_i{y}_i{x}_i=0\\ & {\nabla }_b=-\sum _i{\alpha }_i{y}_i=0\end{array}$$将据此得到的$w,b$代入上面的拉格朗日最小最大值函数，可将对偶问题简化为：$$\begin{array}{rl}& \underset{\alpha }{\max }\frac{1}{2}{w}^2+\sum _i{\alpha }_i(1-y_i(w{x}_i+b))\\ & =\underset{\alpha }{\max }(\frac{1}{2}{w}^2+\sum _i{\alpha }_i-w\sum _i{\alpha }_i{y}_i{x}_i-b\sum _i{\alpha }_i{y}_i)\\ & =\underset{\alpha }{\max }-\frac{1}{2}(\sum _i{\alpha }_i{y}_i{x}_i{)}^2+\sum _i{\alpha }_i\\ & =\underset{\alpha }{\max }-\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)+\sum _i{\alpha }_i\end{array}$$这是典型的满足$\alpha \ge 0$条件下的二次规划问题，有成熟的求解方案。通过对偶问题的转换，有如下好处:
(1) 无须直接求解可能无穷维的特征空间参数$w$，而只需求解数据样本量维度的广义拉格朗日算子空间$\alpha$。
(2) 原来的特征空间通过内积$x_i{x}_j$形式隐式表达，便于以后核技巧的引入。

三、线性可分最优化问题的最优解

根据SVM算法（一）预备知识中的推导，对偶问题的解不大于原始问题的解。而若满足强对偶，则两个最优问题同解，则可以直接通过求解对偶问题得到最优解。
在SVM问题中，必然存在最佳分割面意外的点，即满足Scaler条件（存在点$x_i$，使得$y_i(w{x}_i+b)>1$），因此可通过KKT条件求得最优解：
$$\begin{array}{rl}& {\nabla }_{w}L(w^{\ast },b^{\ast },{\alpha }^{\ast })=w^{\ast }-\sum _i{\alpha }_i^{\ast }{y}_i{x}_i=0\\ & {\nabla }_{b}L(w^{\ast },b^{\ast },{\alpha }^{\ast })=-\sum _i{\alpha }_i^{\ast }{y}_i=0\\ & {\alpha }_i^{\ast }(1-y_i(w^{\ast }{x}_i+b^{\ast }))=0\\ & {\alpha }_i^{\ast }\ge 0\\ & 1-y_i(w^{\ast }{x}_i+b)\le 0\end{array}$$
注意若$\alpha$均为0，则$w^{\ast }=0$，而这并非原问题的解。因此必存在某个${\alpha }_j\ne 0$，此时的$1-y_j(w^{\ast }{x}_j+b)=0$，而$y_j\in \{-1,1\}$，可得$b^{\ast }=y_j-w^{\ast }{x}_j$。由此，可得到基于KKT条件的对偶问题完整的最优解：$$\begin{array}{rl}& w^{\ast }=\sum _i{\alpha }_i^{\ast }{x}_i{y}_i\\ & b^{\ast }=y_j-w^{\ast }{x}_j,if{\alpha }_j^{\ast }>0\end{array}$$而${\alpha }^{\ast }$可通过求解$\underset{\alpha }{\max }-\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)+\sum _i{\alpha }_i$的二次规划问题求解得到。
而判断样本点$x_k$的分类可根据$sign(w^{\ast }{x}_k+b^{\ast })$判断。

这里完整总结下基于广义拉格朗日对偶问题求解SVM问题的基本思路和流程：
（1）求解$\underset{\alpha }{\max }-\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{x}_j)+\sum _i{\alpha }_i$，得到最优的${\alpha }^{\ast }$，其中的样本内积$x_i{x}_j$可通过Gram矩阵进行存储；
（2）选择${\alpha }^{\ast }$中的非零项，记作${\alpha }^{{\ast }^{\prime }}$
（3）根据$w^{\ast }=\sum _i{\alpha }_i^{\ast }{x}_i{y}_i$得到最优系数$w^{\ast }$
（4）选择任意一个${\alpha }_j\in {\alpha }^{{\ast }^{\prime }}$，根据$b^{\ast }=y_j-w^{\ast }{x}_j$得到最优的偏置项$b^{\ast }$
不难发现，$w^{\ast },b^{\ast }$的取值仅与${\alpha }_i>0$处的若干样本点有关，即这些点处$1-y_i(w^{\ast }{x}_i+b^{\ast })=0$，从几何意义上来说，这些点位于分隔面上，所以称为支持向量（support vector）。

四、线性可分SVM问题和感知机问题的关系

对比线性SVM问题的对偶求解和感知机问题的对偶求解，不难发现两者在表达方式上很雷同：
（1）均是基于样本驱动的算法，即可以通过样本点乘积$x_i{y}_i$的线性组合得到目标的$w$
（2）区别在于SVM中的$\alpha$是通过求解二次规划得到，而MLP中的$\alpha$是该点错误的次数。
（3）对偶问题均为原始问题的等效转化。前者

五、依旧留存的问题

上文已经较好的给出了线性可分SVM问题的解法，但仍存在存在如下不足：
（1）在计算${\alpha }^{\ast }$的过程中应用到样本特征内积$x_i{x}_j$，在特征空间维度较小情况下还能够计算，但若特征维度很大，则数据的计算和保存的空间性和时间性都将难以满足。
（2）整个推导的大前提是：数据线性可分。若该条件并不满足，如数据线性不可分割，或数据非线性呢？
后面的文章中将分别通过软间隔、特征非线性变换以及核技巧等方法，来解决这些问题，从而使得SVM算法更加普适。