Pytorch——卷积网络基础

Pytorch——卷积网络基础

1. 二维卷积层

在CNN模型，最常见的是二维的卷积层，我们也从这个方面开始介绍。

1.1 知识回顾

在二维的卷积层中，一个二维输入数组和一个二维核数组通过互相关运算输出一个二维数组。举一个具体的例子来说：

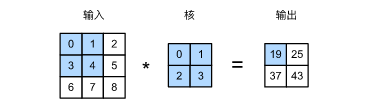
这里定义原始的二维矩阵为33的矩阵，定义卷积核为22，通过卷积核在原始矩阵上的滑动来进行互运算，以蓝色的部分为例：
$$0\ast 0+1\ast 1+3\ast 2+4\ast 3=19$$
在二维的互运算中，卷积核从原始的输入矩阵从左上方开始，按从左向右，从上往下的顺序，依次在输入数组上滑动。当卷积核滑动到某一个位置的时候，窗口输入的子矩阵和卷积核按照元素相乘并求和，得到输出矩阵对应位置的元素。

我们手动的来实现一下这种计算方式：

#encoding=utf-8
import torch
import torch.nn as nn

def corr2d(X,k):
    '''

    :param X: 原始输入矩阵
    :param k: 卷积核
    :return:
    '''
    h,w = k.shape  # 卷积核的维度
    Y = torch.zeros((X.shape[0] - h + 1,X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j] = (X[i:i+h,j:j+w] * k).sum()
    return Y

if __name__ == '__main__':
    X = torch.tensor([[0,1,2],[3,4,5],[6,7,8]])
    k = torch.tensor([[0,1],[2,3]])
    res = corr2d(X,k)
    print(res)

进一步，二维的卷积层将输入和卷积核做互相关运算，并加上一个标量偏差来得到输出。卷积层模型参数包括卷积核和标量偏差。在训练过程中，首先对卷积核内部的参数进行随机的初始化，然后在迭代的过程中对卷积的参数进行调参优化。我们自定义一个卷积层：

class Conv2D(nn.Module):
    def __init__(self,kernel_size):
        super(Conv2D,self).__init__()
        self.weight = nn.Parameter(torch.randn(kernel_size))
        self.bias = nn.Parameter(torch.randn(1))
    def forward(self,x):
        return corr2d(X,self.weight) + self.bias

基于卷积层，我们来实现一个简单的应用：检测图像中物体的边缘，即找到像素变化的位置。首先，构造出一个6*8的图像，它中间4列为黑(用0表示)，其余的位置为白(用1表示)。

#encoding=utf-8
import torch
import torch.nn as nn

def corr2d(X,k):
    '''

    :param X: 原始输入矩阵
    :param k: 卷积核
    :return:
    '''
    h,w = k.shape  # 卷积核的维度
    Y = torch.zeros((X.shape[0] - h + 1,X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j] = (X[i:i+h,j:j+w] * k).sum()
    return Y
class Conv2D(nn.Module):
    def __init__(self,kernel_size):
        super(Conv2D,self).__init__()
        self.weight = nn.Parameter(torch.randn(kernel_size))
        self.bias = nn.Parameter(torch.randn(1))
    def forward(self,x):
        return corr2d(X,self.weight) + self.bias
# 构建图片
X = torch.ones(6,8)
X[:,2:6] = 0


#构建卷积核
K = torch.tensor([[1,-1]],dtype=torch.float32)
Y = corr2d(X,K)

#设置超参数
step = 20
lr = 0.01
conv2d = Conv2D(kernel_size=(1,2))

if __name__ == '__main__':
   for i in range(step):
       Y_hat = conv2d(X)
       loss_vlaue = ((Y_hat- Y) ** 2 ).sum()
       loss_vlaue.backward()

       #梯度下降
       conv2d.weight.data -= lr * conv2d.weight.grad
       conv2d.bias.data -= lr * conv2d.bias.grad

       #梯度清0
       conv2d.weight.grad.fill_(0)
       conv2d.bias.grad.fill_(0)

       if(i+1) % 5 == 0:
           print("Step %d. loss %.3f" %(i+1,loss_vlaue.item()))

1.2. 特征图和感受野

二维的卷积层输出的二维数组可以看做是输入在某一个向量空间中的一个表征，也称为特征图。影响元素x的前向计算的所有可能输入区域（也就是卷积核划过的部分，可能大于原始矩阵X）称为X的感受野。以下图为例：

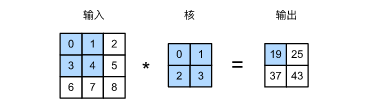
其中输入层的感受野为9，当我们使用卷积核在输出上进行卷积的时候，感受野为4。通过不断的增加卷积层的深度，可以不断地扩大感受野。

1.3 Padding和步长

Padding是指在输入高和宽两侧填充元素(一般是0元素)，依然以上面的图为例子，经过一个padding_size=1之后，结果如下图所示：

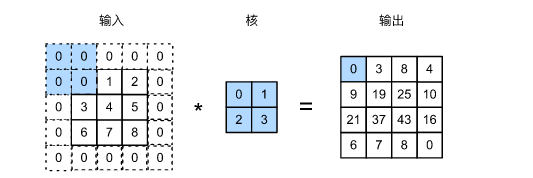
如果不进行padding，则获得的结果矩阵为：
$$(n_k-k_h+1)\ast (n_k-k_w+1)$$
如果使用了padding进行填充，则获得的结果矩阵为：
$$(n_k-k_h+p_h+1)\ast (n_k-k_w+p_w+1)$$

其中$(n_k.n_w)$为原始矩阵的维度，$(k_h,k_w)$表示卷积核的维度，$(p_h,p_w)$为padding的维度。这里我们举一个经过padding之后的计算实例

#encoding=utf-8
import torch
import torch.nn as nn

def corr2d(X,k):
    '''

    :param X: 原始输入矩阵
    :param k: 卷积核
    :return:
    '''
    h,w = k.shape  # 卷积核的维度
    Y = torch.zeros((X.shape[0] - h + 1,X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j] = (X[i:i+h,j:j+w] * k).sum()
    return Y
class Conv2D(nn.Module):
    def __init__(self,kernel_size):
        super(Conv2D,self).__init__()
        self.weight = nn.Parameter(torch.randn(kernel_size))
        self.bias = nn.Parameter(torch.randn(1))
    def forward(self,x):
        return corr2d(X,self.weight) + self.bias

def comp_conv2d(conv2d,X):
    # 定义batch 和 channel的数量
    X = X.view((1,1) + X.shape)
    print(X.shape)
    Y = conv2d(X)
    return Y.view(Y.shape[2:])




if __name__ == '__main__':
    cov2d = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3,padding=1)
    conv2d = nn.Conv2d(in_channels=1,out_channels=1,kernel_size=(5,3),padding=(2,1))
    X = torch.rand(8,8)
    sha = comp_conv2d(conv2d=conv2d,X=X).shape
    print(sha)

这里我们使用到了nn.Conv2d()，这是torch内部自带的二维卷积层，其常用参数情况如下所示：

1. in_channels (int): 输入通道数
2. out_channels (int): 输出通道数
3. kernel_size (int or tuple): 卷积核的维度，两种输入方式，标量(正方形的卷积核)，元组(长方形)
4. stride (int or tuple, optional): 步长，卷积核每次滑动移动的距离。
5. padding (int or tuple, optional): padding填充的默认为0，输入为标量在上下和左右使用相同的值填充，输入为元组，则使用不同的值进行填充。
6. bias (bool, optional): 是否使用偏置项，默认为True

对于卷积还可以使用nn.Conv1d(一维卷积)，nn.Conv3d(三维卷积)，空间维度不同，单操作方式相同，参数也类似，这里就不在赘述了。

在这一节的最后，我们来关注一下步长的问题，步长决定了卷积核每次滑动的距离，我们在使用nn自带的卷积层的时候，在初始化的过程中，通过定义stride来进行确定，默认值为1。

1.4 输入通道和输出通道

这里我们不介绍概念，只是介绍一些在实现的时候，需要注意的问题：

1. 当输入的数据包含多个通道的时候，我们构建的卷积核需要和输入通道数相同通道个数。假设输入数据的通道数为C，则卷积核的通道数也为C。假设卷积核的维度为$(C,k_h,k_w)$，也就是我们在每一个通道上分配一个卷积矩阵$(k_h,k_w)$，最后将各个通道的值相加，举一个2个输入通道的计算：

最后我们使用代码来实现这个计算过程：

def corr2d(X,k):
    '''

    :param X: 原始输入矩阵
    :param k: 卷积核
    :return:
    '''
    h,w = k.shape  # 卷积核的维度
    Y = torch.zeros((X.shape[0] - h + 1,X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j] = (X[i:i+h,j:j+w] * k).sum()
    return Y
def corr2d_multi_in(X,K):
    res = corr2d(X[0,:,:],K[0,:,:])
    for i in range(1,X.shape[0]):
        res += corr2d(X[i,:,:],K[i,:,:])
    return res
if __name__ == '__main__':
    X = torch.tensor([[[0, 1, 2], [3, 4, 5], [6, 7, 8]],
                      [[1, 2, 3], [4, 5, 6], [7, 8, 9]]])
    K = torch.tensor([[[0, 1], [2, 3]], [[1, 2], [3, 4]]])

    res = corr2d_multi_in(X, K)
    print(res)

2. 当有多个输入通道的时候，我们对于各个通道的计算结果作了累积，所以无论输入通道的数量有多少，输出的通道数量总是1。与多输入通道类似，我们也可以定义多个输出通道。设卷积核输入通道数量和输出通道的数量分别为$C_i,C_o$，高和宽分别为$K_h,K_w$，如果希望输出多个通道，我们可以为每一个输出通道分别创建一个$C_i\ast K_h\ast K_w$的卷积核。在卷积计算之后，每一个输出通道上的结果通过卷积核在该输出通道上的卷积核与整个输入计算得到。最后将$C_o$个计算结果进行组合。为了便于矩阵操作，我们直接定义卷积核维度为$C_o\ast C_i\ast K_h\ast K_w$，这样避免了后续的拼接操作。
3. 在本节的最后，我们来关注一种特殊的卷积，即卷积核为1*1的多通道卷积层。对这种卷积，不需要进行padding，得到的卷积结果和输入的结果相同。
   

1.5 池化层

和卷积层类似，池化层每次输入数据的一个固定形状的范围中的元素进行计算。而与卷积核不同的是，池化核内部没有参数，一般是对范围内部的数据取平均值或者最大值。这种运算也称为最大池化或者平均池化。池化核的运动方式和卷积和的运动方式类似，从左上方开始，从左往右，从上往下的顺序，依次在输入矩阵上进行滑动。我们以一个取最大值的例子来展示一下：

与卷积相似的是，pooling层也可以进行padding和stride的操作。过程类似，这里就不在赘述了。

我们来简单的实现一下pooling的操作：

#encoding=utf-8

import torch
import torch.nn as nn
def pool2d(X,pool_size,mode='max'):
    X = X.float()
    p_h,p_w = pool_size
    Y = torch.zeros(X.shape[0] - p_h + 1,X.shape[1] - p_w +1)
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i,j] = X[i:i+p_h,j:j+p_w].max()
            elif mode == 'avg':
                Y[i,j] = X[i:i+p_h,j:j+p_w].mean()
    return Y

if __name__ == '__main__':
    X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
    res = pool2d(X, (2, 2))
    print(res)
    res2 = pool2d(X,(2,2),'avg')
    print(res2)

在本节的最后，我们来看一下在nn模块中的池化操作，在nn中的池化包括：

1. MaxPool ：最大池化(kernel_size, stride=None, padding=0)
   参数1：核size
   参数2：步长
   参数3；padding值。
   对于MaxPool包括1,2,3三个维度。
2. Avg：平均池化(ernel_size, stride=None, padding=0)
   参数1：核size
   参数2：步长
   参数3；padding值。
3. FractionalMaxPool2d，由目标输出大小决定随机步长，在范围内部进行最大池化。
   参数kernel_size- 最大池化操作时的窗口大小。
   参数output_size - 输出图像的尺寸。
   参数output_ratio – 将输入图像的大小的百分比指定为输出图片的大小，范围在(0,1)之间
4. LPPool 幂平均池化操作
5. AdaptiveMaxPool 自适应的最大池化
6. AdaptiveAvgPool 自适应平局池化

2 总结

在这一节中主要是对一般的卷积过程的总结和实现。主要描述了使用Pytorch来实现一般的卷积过程，同时叙述了在nn模块中的卷积核池化层的定义和参数描述。

3 参考

1. 动手学深度学习—Pytorch版