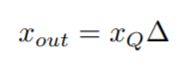Pytorch实现卷积神经网络训练量化（QAT）

本文首发于GiantPandaCV公众号

1. 前言

深度学习在移动端的应用越来越广泛，而移动端相对于GPU服务来讲算力较低并且存储空间也相对较小。基于这一点我们需要为移动端定制一些深度学习网络来满足我们的日常续需求，例如SqueezeNet，MobileNet，ShuffleNet等轻量级网络就是专为移动端设计的。但除了在网络方面进行改进，模型剪枝和量化应该算是最常用的优化方法了。剪枝就是将训练好的大模型的不重要的通道删除掉，在几乎不影响准确率的条件下对网络进行加速。而量化就是将浮点数（高精度）表示的权重和偏置用低精度整数（常用的有INT8）来近似表示，在量化到低精度之后就可以应用移动平台上的优化技术如NEON对计算过程进行加速，并且原始模型量化后的模型容量也会减少，使其能够更好的应用到移动端环境。但需要注意的问题是，将高精度模型量化到低精度必然会存在一个精度下降的问题，如何获取性能和精度的TradeOff很关键。

这篇文章是介绍使用Pytorch复现这篇论文：https://arxiv.org/abs/1806.08342 的一些细节并给出一些自测实验结果。注意，代码实现的是Quantization Aware Training ，而后量化 Post Training Quantization 后面可能会再单独讲一下。代码实现是来自666DZY666博主实现的https://github.com/666DZY666/model-compression。

2. 对称量化

在上次的视频中梁德澎作者已经将这些概念讲得非常清楚了，如果不愿意看文字表述可以移步到这个视频链接下观看视频：深度学习量化技术科普 。然后直接跳到第四节，但为了保证本次故事的完整性，我还是会介绍一下这两种量化方式。

对称量化的量化公式如下：

其中$\Delta$表示量化的缩放因子，$x$和$x_{int}$分别表示量化前和量化后的数值。这里通过除以缩放因子接取整操作就把原始的浮点数据量化到了一个小区间中，比如对于有符号的8Bit 就是$[-128,127]$（无符号就是0到255了）。

这里有个Trick，即对于权重是量化到$[-127,127]$，这是为了累加的时候减少溢出的风险。

因为8bit的取值区间是[-2^7, 2^7-1]，两个8bit相乘之后取值区间是 (-2^14,2^14]，累加两次就到了(-2^15，2^15]，所以最多只能累加两次而且第二次也有溢出风险，比如相邻两次乘法结果都恰好是2^14会超过2^15-1（int16正数可表示的最大值）。

所以把量化之后的权值限制在（-127,127）之间，那么一次乘法运算得到结果永远会小于-128*-128 = 2^14。

对应的反量化公式为：

即将量化后的值乘以$\Delta$就得到了反量化的结果，当然这个过程是有损的，如下图所示，橙色线表示的就是量化前的范围$[rmin,rmax]$，而蓝色线代表量化后的数据范围$[-128,127]$，注意权重取$-127$。

我们看一下上面橙色线的第$4$个黑色圆点对应的float32值，将其除以缩放系数就量化为了一个在$[124,125]$之间的值，然后取整之后就是$125$，如果是反量化就乘以缩放因子返回上面的第$5$个黑色圆点 ，用这个数去代替以前的数继续做网络的Forward。

那么这个缩放系数$\Delta$是怎么取的呢？如下式：

3. 非对称量化

非对称量化相比于对称量化就在于多了一个零点偏移。一个float32的浮点数非对称量化到一个int8的整数（如果是有符号就是$[-128,127]$，如果是无符号就是$[0,255]$）的步骤为 缩放，取整，零点偏移，和溢出保护，如下图所示：

然后缩放系数$\Delta$和零点偏移的计算公式如下：

$\Delta =(rmax-rmin)/255$

$z=int(-rmin/\Delta )$

4. 中部小结

将上面两种算法直接应用到各个网络上进行量化后(训练后量化PTQ)测试模型的精度结果如下：

5. 训练模拟量化

我们要在网络训练的过程中模型量化这个过程，然后网络分前向和反向两个阶段，前向阶段的量化就是第二节和第三节的内容。不过需要特别注意的一点是对于缩放因子的计算，权重和激活值的计算方法现在不一样了。

对于权重缩放因子还是和第2,3节的一致，即：

weight scale = max(abs(weight)) / 127

但是对于激活值的缩放因子计算就不再是简单的计算最大值，而是在训练过程中通过滑动平均（EMA）的方式去统计这个量化范围，更新的公式如下：

moving_max = moving_max * momenta + max(abs(activation)) * (1- momenta)

其中，momenta取接近1的数就可以了，在后面的Pytorch实验中取0.99，然后缩放因子：

activation scale = moving_max /128

然后反向传播阶段求梯度的公式如下：

我们在反向传播时求得的梯度是模拟量化之后权值的梯度，用这个梯度去更新量化前的权值。

这部分的代码如下，注意我们这个实验中是用float32来模拟的int8，不具有真实的板端加速效果，只是为了验证算法的可行性：

class Quantizer(nn.Module):
    def __init__(self, bits, range_tracker):
        super().__init__()
        self.bits = bits
        self.range_tracker = range_tracker
        self.register_buffer('scale', None)      # 量化比例因子
        self.register_buffer('zero_point', None) # 量化零点

    def update_params(self):
        raise NotImplementedError

    # 量化
    def quantize(self, input):
        output = input * self.scale - self.zero_point
        return output

    def round(self, input):
        output = Round.apply(input)
        return output

    # 截断
    def clamp(self, input):
        output = torch.clamp(input, self.min_val, self.max_val)
        return output

    # 反量化
    def dequantize(self, input):
        output = (input + self.zero_point) / self.scale
        return output

    def forward(self, input):
        if self.bits == 32:
            output = input
        elif self.bits == 1:
            print('！Binary quantization is not supported ！')
            assert self.bits != 1
        else:
            self.range_tracker(input)
            self.update_params()
            output = self.quantize(input)   # 量化
            output = self.round(output)
            output = self.clamp(output)     # 截断
            output = self.dequantize(output)# 反量化
        return output

6. 代码实现

基于https://github.com/666DZY666/model-compression/blob/master/quantization/WqAq/IAO/models/util_wqaq.py 进行实验，这里实现了对称和非对称量化两种方案。需要注意的细节是，对于权值的量化需要分通道进行求取缩放因子，然后对于激活值的量化整体求一个缩放因子，这样效果最好（论文中提到）。

这部分的代码实现如下：

# ********************* range_trackers(范围统计器，统计量化前范围) *********************
class RangeTracker(nn.Module):
    def __init__(self, q_level):
        super().__init__()
        self.q_level = q_level

    def update_range(self, min_val, max_val):
        raise NotImplementedError

    @torch.no_grad()
    def forward(self, input):
        if self.q_level == 'L':    # A,min_max_shape=(1, 1, 1, 1),layer级
            min_val = torch.min(input)
            max_val = torch.max(input)
        elif self.q_level == 'C':  # W,min_max_shape=(N, 1, 1, 1),channel级
            min_val = torch.min(torch.min(torch.min(input, 3, keepdim=True)[0], 2, keepdim=True)[0], 1, keepdim=True)[0]
            max_val = torch.max(torch.max(torch.max(input, 3, keepdim=True)[0], 2, keepdim=True)[0], 1, keepdim=True)[0]
            
        self.update_range(min_val, max_val)
class GlobalRangeTracker(RangeTracker):  # W,min_max_shape=(N, 1, 1, 1),channel级,取本次和之前相比的min_max —— (N, C, W, H)
    def __init__(self, q_level, out_channels):
        super().__init__(q_level)
        self.register_buffer('min_val', torch.zeros(out_channels, 1, 1, 1))
        self.register_buffer('max_val', torch.zeros(out_channels, 1, 1, 1))
        self.register_buffer('first_w', torch.zeros(1))

    def update_range(self, min_val, max_val):
        temp_minval = self.min_val
        temp_maxval = self.max_val
        if self.first_w == 0:
            self.first_w.add_(1)
            self.min_val.add_(min_val)
            self.max_val.add_(max_val)
        else:
            self.min_val.add_(-temp_minval).add_(torch.min(temp_minval, min_val))
            self.max_val.add_(-temp_maxval).add_(torch.max(temp_maxval, max_val))
class AveragedRangeTracker(RangeTracker):  # A,min_max_shape=(1, 1, 1, 1),layer级,取running_min_max —— (N, C, W, H)
    def __init__(self, q_level, momentum=0.1):
        super().__init__(q_level)
        self.momentum = momentum
        self.register_buffer('min_val', torch.zeros(1))
        self.register_buffer('max_val', torch.zeros(1))
        self.register_buffer('first_a', torch.zeros(1))

    def update_range(self, min_val, max_val):
        if self.first_a == 0:
            self.first_a.add_(1)
            self.min_val.add_(min_val)
            self.max_val.add_(max_val)
        else:
            self.min_val.mul_(1 - self.momentum).add_(min_val * self.momentum)
            self.max_val.mul_(1 - self.momentum).add_(max_val * self.momentum)

其中self.register_buffer这行代码可以在内存中定一个常量，同时，模型保存和加载的时候可以写入和读出，即这个变量不会参与反向传播。

pytorch一般情况下，是将网络中的参数保存成orderedDict形式的，这里的参数其实包含两种，一种是模型中各种module含的参数，即nn.Parameter,我们当然可以在网络中定义其他的nn.Parameter参数，另一种就是buffer,前者每次optim.step会得到更新，而不会更新后者。

另外，由于卷积层后面经常会接一个BN层，并且在前向推理时为了加速经常把BN层的参数融合到卷积层的参数中，所以训练模拟量化也要按照这个流程。即，我们首先需要把BN层的参数和卷积层的参数融合，然后再对这个参数做量化，具体过程可以借用德澎的这页PPT来说明：

因此，代码实现包含两个版本，一个是不融合BN的训练模拟量化，一个是融合BN的训练模拟量化，而关于为什么融合之后是上图这样的呢？请看下面的公式：

$y=Wx+b$

$y_{bn}=\gamma (\frac{y-\mu }{\sigma })+\beta$

$=\gamma (\frac{Wx+b-\mu }{\sigma })+\beta$

$=\gamma \frac{Wx}{\sigma }+\gamma \frac{b-\mu }{\sigma }+\beta$

所以：

$W_{merge}=\gamma \frac{W}{\sigma }$

$b_{merge}=\gamma \frac{b-\mu }{\sigma }+\beta$

公式中的，$W$和$b$分别表示卷积层的权值与偏置，$x$和$y$分别为卷积层的输入与输出，则根据$BN$的计算公式，可以推出融合了batchnorm参数之后的权值与偏置，$W_{merge}$和$b_{merge}$。

未融合BN的训练模拟量化代码实现如下（带注释）：

# ********************* 量化卷积（同时量化A/W，并做卷积） *********************
class Conv2d_Q(nn.Conv2d):
    def __init__(
        self,
        in_channels,
        out_channels,
        kernel_size,
        stride=1,
        padding=0,
        dilation=1,
        groups=1,
        bias=True,
        a_bits=8,
        w_bits=8,
        q_type=1,
        first_layer=0,
    ):
        super().__init__(
            in_channels=in_channels,
            out_channels=out_channels,
            kernel_size=kernel_size,
            stride=stride,
            padding=padding,
            dilation=dilation,
            groups=groups,
            bias=bias
        )
        # 实例化量化器（A-layer级，W-channel级）
        if q_type == 0:
            self.activation_quantizer = SymmetricQuantizer(bits=a_bits, range_tracker=AveragedRangeTracker(q_level='L'))
            self.weight_quantizer = SymmetricQuantizer(bits=w_bits, range_tracker=GlobalRangeTracker(q_level='C', out_channels=out_channels))
        else:
            self.activation_quantizer = AsymmetricQuantizer(bits=a_bits, range_tracker=AveragedRangeTracker(q_level='L'))
            self.weight_quantizer = AsymmetricQuantizer(bits=w_bits, range_tracker=GlobalRangeTracker(q_level='C', out_channels=out_channels))
        self.first_layer = first_layer

    def forward(self, input):
        # 量化A和W
        if not self.first_layer:
            input = self.activation_quantizer(input)
        q_input = input
        q_weight = self.weight_quantizer(self.weight) 
        # 量化卷积
        output = F.conv2d(
            input=q_input,
            weight=q_weight,
            bias=self.bias,
            stride=self.stride,
            padding=self.padding,
            dilation=self.dilation,
            groups=self.groups
        )
        return output

而考虑了折叠BN的代码实现如下（带注释）：

def reshape_to_activation(input):
  return input.reshape(1, -1, 1, 1)
def reshape_to_weight(input):
  return input.reshape(-1, 1, 1, 1)
def reshape_to_bias(input):
  return input.reshape(-1)
# ********************* bn融合_量化卷积（bn融合后，同时量化A/W，并做卷积） *********************
class BNFold_Conv2d_Q(Conv2d_Q):
    def __init__(
        self,
        in_channels,
        out_channels,
        kernel_size,
        stride=1,
        padding=0,
        dilation=1,
        groups=1,
        bias=False,
        eps=1e-5,
        momentum=0.01, # 考虑量化带来的抖动影响,对momentum进行调整(0.1 ——> 0.01),削弱batch统计参数占比，一定程度抑制抖动。经实验量化训练效果更好,acc提升1%左右
        a_bits=8,
        w_bits=8,
        q_type=1,
        first_layer=0,
    ):
        super().__init__(
            in_channels=in_channels,
            out_channels=out_channels,
            kernel_size=kernel_size,
            stride=stride,
            padding=padding,
            dilation=dilation,
            groups=groups,
            bias=bias
        )
        self.eps = eps
        self.momentum = momentum
        self.gamma = Parameter(torch.Tensor(out_channels))
        self.beta = Parameter(torch.Tensor(out_channels))
        self.register_buffer('running_mean', torch.zeros(out_channels))
        self.register_buffer('running_var', torch.ones(out_channels))
        self.register_buffer('first_bn', torch.zeros(1))
        init.uniform_(self.gamma)
        init.zeros_(self.beta)
        
        # 实例化量化器（A-layer级，W-channel级）
        if q_type == 0:
            self.activation_quantizer = SymmetricQuantizer(bits=a_bits, range_tracker=AveragedRangeTracker(q_level='L'))
            self.weight_quantizer = SymmetricQuantizer(bits=w_bits, range_tracker=GlobalRangeTracker(q_level='C', out_channels=out_channels))
        else:
            self.activation_quantizer = AsymmetricQuantizer(bits=a_bits, range_tracker=AveragedRangeTracker(q_level='L'))
            self.weight_quantizer = AsymmetricQuantizer(bits=w_bits, range_tracker=GlobalRangeTracker(q_level='C', out_channels=out_channels))
        self.first_layer = first_layer

    def forward(self, input):
        # 训练态
        if self.training:
            # 先做普通卷积得到A，以取得BN参数
            output = F.conv2d(
                input=input,
                weight=self.weight,
                bias=self.bias,
                stride=self.stride,
                padding=self.padding,
                dilation=self.dilation,
                groups=self.groups
            )
            # 更新BN统计参数（batch和running）
            dims = [dim for dim in range(4) if dim != 1]
            batch_mean = torch.mean(output, dim=dims)
            batch_var = torch.var(output, dim=dims)
            with torch.no_grad():
                if self.first_bn == 0:
                    self.first_bn.add_(1)
                    self.running_mean.add_(batch_mean)
                    self.running_var.add_(batch_var)
                else:
                    self.running_mean.mul_(1 - self.momentum).add_(batch_mean * self.momentum)
                    self.running_var.mul_(1 - self.momentum).add_(batch_var * self.momentum)
            # BN融合
            if self.bias is not None:  
              bias = reshape_to_bias(self.beta + (self.bias -  batch_mean) * (self.gamma / torch.sqrt(batch_var + self.eps)))
            else:
              bias = reshape_to_bias(self.beta - batch_mean  * (self.gamma / torch.sqrt(batch_var + self.eps)))# b融batch
            weight = self.weight * reshape_to_weight(self.gamma / torch.sqrt(self.running_var + self.eps))     # w融running
        # 测试态
        else:
            #print(self.running_mean, self.running_var)
            # BN融合
            if self.bias is not None:
              bias = reshape_to_bias(self.beta + (self.bias - self.running_mean) * (self.gamma / torch.sqrt(self.running_var + self.eps)))
            else:
              bias = reshape_to_bias(self.beta - self.running_mean * (self.gamma / torch.sqrt(self.running_var + self.eps)))  # b融running
            weight = self.weight * reshape_to_weight(self.gamma / torch.sqrt(self.running_var + self.eps))  # w融running
        
        # 量化A和bn融合后的W
        if not self.first_layer:
            input = self.activation_quantizer(input)
        q_input = input
        q_weight = self.weight_quantizer(weight) 
        # 量化卷积
        if self.training:  # 训练态
          output = F.conv2d(
              input=q_input,
              weight=q_weight,
              bias=self.bias,  # 注意，这里不加bias（self.bias为None）
              stride=self.stride,
              padding=self.padding,
              dilation=self.dilation,
              groups=self.groups
          )
          # （这里将训练态下，卷积中w融合running参数的效果转为融合batch参数的效果）running ——> batch
          output *= reshape_to_activation(torch.sqrt(self.running_var + self.eps) / torch.sqrt(batch_var + self.eps))
          output += reshape_to_activation(bias)
        else:  # 测试态
          output = F.conv2d(
              input=q_input,
              weight=q_weight,
              bias=bias,  # 注意，这里加bias，做完整的conv+bn
              stride=self.stride,
              padding=self.padding,
              dilation=self.dilation,
              groups=self.groups
          )
        return output

注意一个点，在训练的时候bias设置为None，即训练的时候不量化bias。

7. 实验结果

在CIFAR10做Quantization Aware Training实验，网络结构为：

import torch
import torch.nn as nn
import torch.nn.functional as F
from .util_wqaq import Conv2d_Q, BNFold_Conv2d_Q

class QuanConv2d(nn.Module):
    def __init__(self, input_channels, output_channels,
            kernel_size=-1, stride=-1, padding=-1, groups=1, last_relu=0, abits=8, wbits=8, bn_fold=0, q_type=1, first_layer=0):
        super(QuanConv2d, self).__init__()
        self.last_relu = last_relu
        self.bn_fold = bn_fold
        self.first_layer = first_layer

        if self.bn_fold == 1:
            self.bn_q_conv = BNFold_Conv2d_Q(input_channels, output_channels,
                    kernel_size=kernel_size, stride=stride, padding=padding, groups=groups, a_bits=abits, w_bits=wbits, q_type=q_type, first_layer=first_layer)
        else:
            self.q_conv = Conv2d_Q(input_channels, output_channels,
                    kernel_size=kernel_size, stride=stride, padding=padding, groups=groups, a_bits=abits, w_bits=wbits, q_type=q_type, first_layer=first_layer)
            self.bn = nn.BatchNorm2d(output_channels, momentum=0.01) # 考虑量化带来的抖动影响,对momentum进行调整(0.1 ——> 0.01),削弱batch统计参数占比，一定程度抑制抖动。经实验量化训练效果更好,acc提升1%左右
        self.relu = nn.ReLU(inplace=True)

    def forward(self, x):
        if not self.first_layer:
            x = self.relu(x)
        if self.bn_fold == 1:
            x = self.bn_q_conv(x)
        else:
            x = self.q_conv(x)
            x = self.bn(x)
        if self.last_relu:
            x = self.relu(x)
        return x

class Net(nn.Module):
    def __init__(self, cfg = None, abits=8, wbits=8, bn_fold=0, q_type=1):
        super(Net, self).__init__()
        if cfg is None:
            cfg = [192, 160, 96, 192, 192, 192, 192, 192]
        # model - A/W全量化(除输入、输出外)
        self.quan_model = nn.Sequential(
                QuanConv2d(3, cfg[0], kernel_size=5, stride=1, padding=2, abits=abits, wbits=wbits, bn_fold=bn_fold, q_type=q_type, first_layer=1),
                QuanConv2d(cfg[0], cfg[1], kernel_size=1, stride=1, padding=0, abits=abits, wbits=wbits, bn_fold=bn_fold, q_type=q_type),
                QuanConv2d(cfg[1], cfg[2], kernel_size=1, stride=1, padding=0, abits=abits, wbits=wbits, bn_fold=bn_fold, q_type=q_type),
                nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
                
                QuanConv2d(cfg[2], cfg[3], kernel_size=5, stride=1, padding=2, abits=abits, wbits=wbits, bn_fold=bn_fold, q_type=q_type),
                QuanConv2d(cfg[3], cfg[4], kernel_size=1, stride=1, padding=0, abits=abits, wbits=wbits, bn_fold=bn_fold, q_type=q_type),
                QuanConv2d(cfg[4], cfg[5], kernel_size=1, stride=1, padding=0, abits=abits, wbits=wbits, bn_fold=bn_fold, q_type=q_type),
                nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
                
                QuanConv2d(cfg[5], cfg[6], kernel_size=3, stride=1, padding=1, abits=abits, wbits=wbits, bn_fold=bn_fold, q_type=q_type),
                QuanConv2d(cfg[6], cfg[7], kernel_size=1, stride=1, padding=0, abits=abits, wbits=wbits, bn_fold=bn_fold, q_type=q_type),
                QuanConv2d(cfg[7], 10, kernel_size=1, stride=1, padding=0, last_relu=1, abits=abits, wbits=wbits, bn_fold=bn_fold, q_type=q_type),
                nn.AvgPool2d(kernel_size=8, stride=1, padding=0),
                )

    def forward(self, x):
        x = self.quan_model(x)
        x = x.view(x.size(0), -1)
        return x

训练Epoch数为30，学习率调整策略为：

def adjust_learning_rate(optimizer, epoch):
    if args.bn_fold == 1:
        if args.model_type == 0:
            update_list = [12, 15, 25]
        else:
            update_list = [8, 12, 20, 25]
    else:
        update_list = [15, 17, 20]
    if epoch in update_list:
        for param_group in optimizer.param_groups:
            param_group['lr'] = param_group['lr'] * 0.1
    return

类型	Acc	备注
原模型(nin)	91.01%	全精度
对称量化, bn不融合	88.88%	INT8
对称量化，bn融合	86.66%	INT8
非对称量化，bn不融合	88.89%	INT8
非对称量化，bn融合	87.30%	INT8

现在不清楚为什么量化后的精度损失了1-2个点，根据德澎在MxNet的实验结果来看，分类任务不会损失精度，所以不知道这个代码是否存在问题，有经验的大佬欢迎来指出问题。

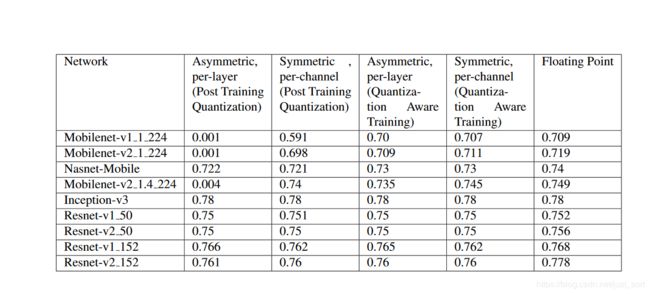
然后白皮书上提供的一些分类网络的训练模拟量化精度情况如下：

注意前面有一些精度几乎为0的数据是因为MobileNet训练出来之后某些层的权重非常接近0，使用训练后量化方法之后权重也为0，这就导致推理后结果完全错误。

8. 总结

今天介绍了一下基于Pytorch实现QAT量化，并用一个小网络测试了一下效果，但比较遗憾的是并没有获得论文中那么理想的数据，仍需要进一步研究。

---

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新，我们成立了一个QQ群，二维码如下，感兴趣可以加入。