期望、方差、标准差、协方差、相关系数、协方差矩阵、残差、残差平方和(SSE)、标准化残差，残差分析

                              通过学习，结合网络上搜索， 把相关概念整理了一下。

1、期望（均值、数学期望）

       期望是 度量数据的集中趋势的一个重要指标，是研究随机变量的一个重要数字特征

     离散型

          随机变量Xi，其对因的概率P(Xi),则有Xi  P(Xi)的和成为离散随机变量的期望。

               Xi: ,对应的概率为：，则：

              

                  

   连续型

         设连续的随机变量X的概率密度函数为f(X)，若积分绝对收敛，则其积分值为该随机变量的期望。

                   

  函数的期望：

          离散：设Y是随机变量X的函数：  （  是连续函数），则：

                      

          连续：(1)、若随机变量Y符合函数  ，且  绝对收敛，则：

                    

 

 2、方差     

         方差是度量随机变量的离散程度重要指标，是研究随机变量的一个重要数字特征。

           方差是在概率论和统计学中衡量随机变量或一组数据时的离散程度的度量，换句化说如果想知道一组数据之间的分散程度的话就可以使用方差来表示。随机变量的波动范围。

         方差：在统计描述中，用来计算每一个变量与总体均值之间的差异

           总体方差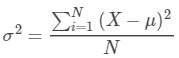：，：总体方差；X：随机变量，：为总体均值；N:总体例数

           样本方差：，S2：样本方差；Xi：样本变量；：为样本均值；N:样本个数

 

3、标准差

        标准差是方差的平方根。

        方差和标准差都是用来衡量随机变量离散程度的量，但二者量纲(单位)不同，标准差和期望属于同一个量纲。在描述波动性时，标准差比方差方便些。

4、协方差

     期望、标准差、方差，是从一维(单个变量)角度去研究随机变量的。

   协方差是两个随机变量的总体误差，是从多维角度去研究随机变量的。

    协方差：是从各个不同维度去度量变量偏离其均值的程度。当协方差为正时，两个变量正相关；为负时，负相关，为0时，不相关。

   方差是协方差的一种特殊情况(x=y)

  设：期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为：

                 

直观上，协方差是两个随机变量总体误差的期望。

协方差与方差、期望之间的关系：

若两个随机变量X和Y相互独立，则E[(X-E(X))(Y-E(Y))]=0，因而若上述数学期望不为零，则X和Y必不是相互独立的，亦即它们之间存在着一定的关系。

协方差与方差关系：

              D(X+Y) = D(X) + D(Y) +2Cov(X,Y)  

              D(X-Y) = D(X) + D(Y) -2Cov(X,Y)       

 协方差与期望关系：

              Cov(X,Y) =E[XY]-E[X]E[Y]             

协方差性质：           

         （1）Cov(X，Y)=Cov(Y，X)；

         （2）Cov(aX，bY)=abCov(X，Y)，（a，b是常数）；

         （3）Cov(X1+X2，Y)=Cov(X1，Y)+Cov(X2，Y)。

          由协方差定义，可以看出Cov(X，X)=D(X)，Cov(Y，Y)=D(Y)。

5、相关系数

       协方差作为描述X和Y相关程度的量，在同一物理量纲之下有一定的作用，但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。为此引入“相关系数”的概念：

           ，xy称为随机变量X，Y的相关系数。

若，xy=0，则称随机变量X、Y不线性相关，xy=0 是Cov(X,Y)=0的充分必要条件，两个随机变量不相关等价于协方差等于零。

     |xy|1；∣ρXY∣=1充分必要条件为P{Y=aX+b}=1，（a，b为常数，a≠0）

6、协方差矩阵

            设  为n维随机变量，称矩阵

                                                                     

                             

                                 为n维随机变量  的协方差矩阵（covariance matrix），也记为  ，其中

                                               

                                   为 的分量  和  的协方差（设它们都存在）。

               设X和Y是随机变量，若E(X^k)，k=1，2，...存在，则称它为X的k阶原点矩，简称k阶矩。

               若E{[X-E(X)]k}，k=1，2，...存在，则称它为X的k阶中心矩。

              若E{(X^k）（Y^p)}，k、p=1，2，...存在，则称它为X和Y的k+p阶混合原点矩。

              若E{[X-E(X)]^k[Y-E(Y)]^l }，k、l=1，2，...存在，则称它为X和Y的k+l阶混合中心矩。

              显然，X的数学期望E(X)是X的一阶原点矩，方差D(X)是X的二阶中心矩，协方差Cov(X，Y)是X和Y的二阶混合中心矩。             

协方差矩阵具有如下性质：

        （1）  

.       （2）  ，其中A是矩阵，b是向量。

        （3）  

 

例如，二维随机变量  的协方差矩阵为

                                 

              其中 

                      

               对角线上分别是X1和X2的方差，非对角线上是协方差。协方差大于0表示X1和X2若有一个增，另一个也增；小于0表示一个增，一个减；协方差为0时，两者独立。协方差绝对值越大，两者对彼此的影响越大，反之越小。

7、残差

           在回归分析过程中，给出了样本的观测值，构建出模型(回归方程)，将观样本测值输入模型计算出估计值(又叫预测值，拟合值)，这个估计值与观测值之间的偏差叫做残差(residual)。残差在误差理论中是一个经常遇到的重要参数。

 

          e表示残差，表示各个观测值，表示估计值(预测值，拟合值)，则有

         残差：是因变量的观测值与根据估计的回归方程求出的预测  之差

         “残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话， 我们可以将残差看作误差的观测值

        残差又可以这样理解：根据n个观察值拟合适当的模型后，余下未能拟合部份()称为残差

   残差特征：

     (1)、回归分析中，，残差 服从正态分布N~(0，)。

     (2)、（e  - 残差平均值)/残差的标准差，成为标准化残差，以e*表示，则e*服从标准正太分布N~(0,1).

     (3)、实验点的标准化残差落在(-2，2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2，2)区间以外，可在95%置信度将其判为异常实验点，不参与回归直线拟合。

8、残差平方和(SSE)、回归平方和(SSR)、总偏离平方和(SST)、均方差(MSE)

       SSE：误差平方和、组内平方和、SSE、和方差、剩余偏差(??);       SSR:回归偏差(??);       SST:总和方差

       MSE:方差

       SST = SSR+SSE    

                                           

       SST:变差总平方和

       SSR：由x与Y之间的线性关系引起的y的变化

       SSE：除x影响之外的其它因素引起y的变化

                                      

                      由上可知，SSR越大，则表示回归预测的越准确，观测点（Xi，Yi）离回归直线约近，也就是SSE越小。

          判定系数（R-square）：         

                         SSR/SST=(SST-SSE)/SST=1 - SSE/SST

                      R-square = 1 - SSE/SST, 判定系数(确实系数,拟合优度)，是相关系数的平方，用来判断模型的对数据拟合的好坏，取值范围[0,1]

 

9、标准化残差

              标准化残差：是残差除以其标准差后得到的数值(见上面残差)。

   (是残差的标准差的估计)

如果误差项  服从正态分布的这一假定成立，则标准化残差的分布也服从正态分布。大约有95%的标准化残差在 -2~2 之间。

                                                 

从图中可以看出，除了箭头所标识的点外，所有的标准化残差都在 -2~2 之间，所以误差项服从正态分布的假定成立

10、残差分析

       残差图是残差分析的主要工具之一。     

常用残差图：有关x残差图，有关的残差图，标准化残差图

有关x残差图：用横轴表示自变量x的值，纵轴表示对应残差 ，每个x的值与对应的残差用图上的一个点来表示。

分析残差图，首先考察残差图的形态及其反映的信息。

                                         

分析：

（a）对所有x值，的方差都相同，且描述变量x和y之间的回归模型是合理的，残差图中的所有点落在一条水平带中间。

（b）对所有的值，的方差是不同的，对于较大的x值，相应的残差也较大，违背了的方差相等的假设

（c）表明所选的回归模型不合理，应考虑曲线回归或多元回归模型。