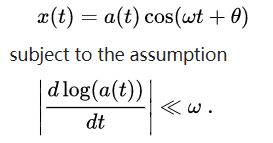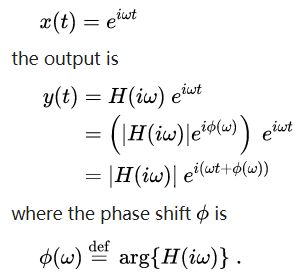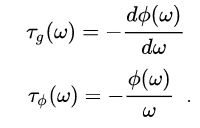群延时和相位延时
翻译自wikipedia
在信号处理中,群延时是信号通过设备各个分量正弦波幅度经历的延时,因此是各正弦波频率的函数。相位延时,与幅度的延时相对照是各分量正弦波相位经过设备的延时。
当信号通过放大器,扬声器或者传输媒介时所有频率分量会产生延时。不同频率分量相位延时是不同的除非设备是线性相位(线性相位和最小相位容易混淆,他们是不同的)。延时变化意味着信号包含的多个频率分量将要遭受不同的失真因为在输出端延时的量不同。足够大的延时变化可能会导致问题例如声音信号保真度低或者从模拟载波解调数字信号导致ISI。高速调制解调用自适应均衡来补偿非恒包络群延时。
介绍
群延时是测量时间失真的而有效方法,通过对被测设备相位响应在频率上做差分来计算。群延时是在任意给定频率相位响应斜率的侧量。群延时的变化导致信号失真,就像线性相位的波动导致失真。
在线性是不变系统理论,控制理论和数字或模拟信号处理中,输入信号和输出信号的关系如下:
h(t)是时域脉冲响应,X(s),Y(s),H(s)是输入信号,输出信号和脉冲响应的拉普拉斯变换。H(s)也叫做线性时不变系统的转移函数,完全的描述了LTI系统的输入输出特性。
假设系统倍一个近似正弦波信号所驱动,即正弦波的幅度包络和正弦波频率相关。数学上意味着信号形式如下:
线性时不变系统的输出可以用如下方程描述:
则 {\displaystyle \displaystyle \tau _{g}}和 {\displaystyle \displaystyle \tau _{\phi }}分别为群延时和相位延时。
在线性相位系统中,和 是恒定的并且相等的,他们共同的值等于系统总体延时。系统的相移是 {\displaystyle \displaystyle -\omega \tau _{\phi }}。
更一般化的,对于转移函数H(s)线性时不变系统假设单位幅度的复数正弦波进入系统
群延时和相位延时基于频率的,可以根据相移phase shift Φ来计算
线性相位:
线性相位指的是相频响应φ(ω)为频率ω的线性函数,数学表示:φ(ω) = a*ω + b
通俗解释是:信号经过滤波器后,各个频率分量的延时时间都是一样的。(此处如果理解着感觉矛盾,看下面群延时的解释)
群延迟:
群延迟= -dφ(ω) / d(ω) = -a
“群延迟”(dφ(ω)/dω)就是相位对频率的微分(导数)。若其是非常数,则波的各频率分量随着时间推移将各自散伙。而若其是个常数——K,则有:
cos(ω t + φ(ω)) = cos(ω t + K ω) = cos(ω(t + K))
表示波的各频率分量延迟了时间 K,保持原形。