数据结构课程设计报告 二叉树的应用
题 目: 二叉树的应用
西 安 邮 电 大 学
(计算机学院)
一. 设计目的
树结构在客观世界中广泛存在, 如人类社会的族谱和各种社会组织机构都可用树形象表示. 在现代的数字通信、数据压缩、等价类问题处理方面,以及在计算机领域中编译系统的语言结构描述,数据库系统的信息组织与检索、操作系统中的文件木iluzuzhijiegou等方面,树型结构均为中演的描述及实现工具。
通过一周的课程设计,用链式存储结构实现对二叉排序树的的创建,各种遍历,树高、节点数量等基本操作,达到巩固和运用理论知识、锻炼实践能力、构件合理知识结构和提高程序设计能力的目的
二. 设计内容
针对这样的问题, 我选择了二叉树的操作作为我的课程设计主题, 编写程序, 实现对二叉树的遍历. 在本次课程设计中, 二叉树的建立使用了递归算法;在前序、中序和后续遍历的算法中则同时使用了递归与非递归的算法, 即在这些遍历算法的实现中使用了栈结构与队列结构, 提供了6种不同的遍历方式, 供使用者选择. 同时, 该程序具有输出层序遍历的功能, 层序遍历模块使用了非递归算法. 该程序基本实现了对二叉树的遍历, 对于递归与非递归算法, 我们应从实际应用中体验这些算法的优越性
编程实现二叉树的建立,先序、中序、后序(递归和非递归方法)、层序遍历,二叉树的高度、繁茂度,交换左右子树,统计叶子节点的数目,判断是否为完全二叉树,按树的形态在屏幕上打印输出。并要求:1) 从文件中读入建树信息,树的节点数目不小于20个,树的高度不小于4;2) 建树信息采用两行英文字符表示,每个英文字符代表一个结点,第1行为树的中序遍历结果,第2行为树的后序遍历结果。
三.概要设计
通过一周的课程设计,用链式存储结构实现对二叉排序树的的创建,各种遍历,树高、节点数量等基本操作,在整个程序中可以将程序分为四大代码块,首先菜单代码块;其次是基础代码块,分别包括栈操作代码块和队列操作代码块;再其次是主体代码块即各种树操作的函数代码块,最后是输出操作代码块。下面是具体介绍。
1. 功能模块图;
2. 各个模块详细的功能描述。
(1)、菜单函数代码块用户使用导航的功能,提示用户如何操作;
(2)、树操作代码块主要是对树的各种操作,也就是本程序的主体部分,主要包括如下函数::
void creat_Btree(BiTree *root,FILE *fp);//创建树
void pre_visit(BiTree root);//非递归先序遍历
void re_pro_visit(BiTree root);//递归先序遍历
void mid_visit(BiTree root);//非递归中序遍历
void re_mid_visit(BiTree root);//递归中序遍历
void post_visit(BiTree root);//非递归先后序遍历
void re_post_visit(BiTree root);//递归先后序遍历
void leval_visit(BiTree root);//层次遍历
BiTree parent (BiTree root,BiTree leaf);//搜索双亲函数
void print_path(BiTree root);//打印路径函数
void swap_tree(BiTree root);//交换左右子树
void post_visit_point(BiTree root);//递归统计有两个孩子节点和至少有一个孩子的节点,间接统计只有一个孩子的节点
int mid_visit_leaf(BiTree root);//输出叶子节点个数和叶子节点
void pro_visit_leaf(BiTree root);//先序统计叶子节点
int postTreeDepth(BiTree root);//求树的深度
void printTree(BiTree root,int h);//打印树
void count_leaf_Level(BiTree root,int k);//某一层k的叶子结点个数(待修改)
void print_count_leaf(BiTree root); //统计每一层的叶子节点个数
int Lush_degree(BiTree root);//二叉树的繁茂度
int IsComBinTree(BiTree root);//判定是否为完全二叉树
其中各个函数之间又存在相互调用关系,共同实现菜单中出现的若干个功能。
(3)栈操作代码块、队列操作代码块以及输出操作代码块主要是担任程序的基础功能搭建,用于辅助树操作代码块实现其相应的功能,本身没有响应用户具体实际操作的要求。
四.详细设计
程序的主体部分是树操作模块,下面就树操作模块进行具体解析:
1. 功能函数的调用关系图
其他功能均为单个函数实现,不做流程描述
2. 各功能函数的数据流程图
3. 重点设计及编码
(1),主函数
int main ()
{
system("title 树操作系统 ");
// int leaf,depth;//叶子节点数和树的深度
FILE *fp;
BiTree root;
fp= file();
creat_Btree(&root,fp);//创建树
point.depth=postTreeDepth(root);
main_menu(root);
return 0;
}
(2)、扩展先序建立二叉树
//递归一次便给当前节点的数据域赋值,然后利用递归
//一次给该结点的左右子树赋值,实现二叉树的创建
void creat_Btree(BiTree *root,FILE *fp)
{
char ch;
ch=fgetc(fp);
if(ch==EOF)
return ;
if(ch=='#')
(*root)=NULL;
else{
(*root)=(BiTree)malloc(sizeof(BiTNode));
(*root)->data=ch;
creat_Btree(&((*root)->Lchild),fp);
creat_Btree(&((*root)->Rchild),fp);
}
}
(3)、非递归后序遍历
/* 首先通过循环不断将节点入栈,直到找到左子树的最左侧的节点,然后取栈顶元素,即该结点,及对其右子树进行考察,
如果其右子树是空或者是已经访问过,则退栈,访问站顶元素,并将其地址赋值给第二辅助标记指针变量,并将第一指
针变量置为空,便于再退栈,访问下一个节点的数据,否则如果该节点的右子树不为空且未被访问过,则同样的访问该节点的右子树。
*/
void post_visit(BiTree root)
{
stack s;
s=init_seq();
BiTree p,q;
p=root;q=NULL;
while(!isempty(s)||p!=NULL)
{
while(p!=NULL)
{
push(s,p);
p=p->Lchild;
}
if(!isempty(s))
{
p=top(s);
if((p->Rchild==NULL)||(p->Rchild==q))
{
pop(s,&p);
visit(p->data);
q=p;
p=NULL;
}
else
p=p->Rchild;
}
}
}
(4)某一层k的叶子结点个数(待修改)并记录树的深度
void count_leaf_Level(BiTree root,int k)
{
BiTree QCountPoint[100];
BiTree bt;
bt=root;
int front,rear;
int last,level;
front=rear=0;
if(bt==NULL||k<1)
return ;
rear++;
QCountPoint[rear]=bt;
last=rear;
level=1;
while(rear!=front)
{
front=front+1;
bt=QCountPoint[front];
if(level==k&&bt->Lchild==NULL&&bt->Rchild==NULL)
point.countleaf[k]++;
if(level==k)
point.countpoint[k]++;
if(bt->Lchild!=NULL)
{
rear=rear+1;
QCountPoint[rear]=bt->Lchild;
}
if(bt->Rchild!=NULL)
{
rear=rear+1;
QCountPoint[rear]=bt->Rchild;
}
if(front==last)
{
level++;
last=rear;
}
if(level>k)
return ;
}
}
五.测试数据及运行结果
1.正常测试数据和运行结果
要求提供3组正常测试数据和运行结果
Figure 1 初始输入菜单 Figure 2遍历输出
Figure 3隔层叶子节点和节点数Figure 4 退出界面
2.异常测试数据及运行结果
要求提供2组异常测试数据和运行结果
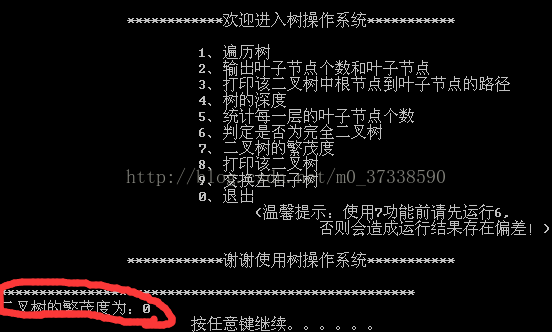
Figure 5 由于输入错误顺序导致繁茂度出错
Figure 6输入错误导致多输出一次
六.调试情况,设计技巧及体会
1.改进方案
对自己的设计进行评价,指出合理和不足之处,提出改进方案;
1) 菜单设置方面:运用了switch()语句,这样虽然看着有条理,却不适合用在二叉树的遍历上,因为遍历结果显而易见并不十分复杂,没有必要使程序复杂化,故采用的是程序运行输出模式。
2) 二叉树的创建:采用文件读取的方式,利用扩展先序遍历实现二叉树的创建,这样做相对简单,但是对有些情况下不太实用,所以应该增加一项根据后序中序实现创建的算法,是程序更加完善。
3) 整体布局:由于存在某两个函数的制约关系,要求必须先执行A在执行B,一旦执行顺序错误就会导致输出结果错误。这样降低了程序的冗错性,不利于用户操作,可以通过添加函数间强制装换关系,强制执行,或者是在后者运行的函数中添加必要语句,使其脱离制约函数的制约。
3. 体会
对于遍历功能主体为非递归算法,我使用了栈结构和队列结构,分别用于前序遍历、中序、后序历、非递归层次序遍历方法中。同时其他的功能的实现也是一站和队列为基础,通过栈和队列的数据的吞吐实现各种变化。使用栈和队列的过程中,我在实践中又学习了栈和队列的一些知识,提高了各种逻辑结构之间的综合运用能力。在后期测试阶段,我参考了许多课程设计案例,大部分都运用了switch()语句,这样虽然看着有条理,但是在制作菜单时有点太过于啰嗦,所以在输入的时候同时借助easyx实现输入,以提高用户的可实用性,更加人性化。
短短一周的课程设计时间很快就过去了,而我所选的“二叉树的应用”设计题目也接近尾声。这期间,有老师的指导,有同学的帮助,有自己不懂就翻阅资料寻求解答的努力。经过磕磕碰碰总算完了任务。虽然所做的程序算不上了自己最满意的,但却是这一个星期以来的努力成果,是这学期学数据结构的总结,是对自己能力的考验,是自己尽最大努力做出来的。
在课程设计的过程当中,是对平时学习的检测,虽然平时书上所讲似乎懂了,就如我所做的“二叉树的应该”一样,但在真正设计起程序来,很多困难还是意想不到的,那只能在设计过程中不断的摸索,在摸索中不断提升自己。
一周课程设计的时间是过去了,但是,对数据结构的学习似乎才是开始,以后要学习的还很多很多,前面要走的路还很远很远。而我也要整装待发,在摸索中前进,在前进中不断摸索,让自己的路走得更远更长!
七.参考文献
[1].《数据结构与算法》 主编:王曙燕 2013年9月第1版 人民邮电出版社
[2].《C语言程序设计教程》主编:王曙燕 2014年9月第1版 人民邮电出版社
源代码如下(不属于报告的一部分):
/* 二叉树的应用(二叉树)
[问题描述]
编程实现二叉树的建立,先序、中序、后序(递归和非递归方法)、层序遍历,二叉树的高度、繁茂度,
交换左右子树,统计叶子节点的数目,判断是否为完全二叉树,按树的形态在屏幕上打印输出。
[基本要求]
(1) 从文件中读入建树信息,树的节点数目不小于20个,树的高度不小于4。
(2) 建树信息采用两行英文字符表示,每个英文字符代表一个结点,第1行为树的中序遍历结果,
第2行为树的后序遍历结果。
[名词注释]
二叉树的繁茂度:为各层结点数的最大值与树的高度的乘积
完全二叉树:
a:所有节点只可能出现在最大的两层上
b:对于任何节点,若其右子树的层高为k,则其左子树可能为k或者是k+1
*/
#include
#include
#include
#include
#include
#include
#include
#define TRUE 1
#define FALSE 0
//树型结构体
typedef struct Node
{
char data;
struct Node *Lchild;
struct Node *Rchild;
}BiTNode,*BiTree;
//栈元素结构体
typedef struct node
{
BiTree tree;
struct node *next;
}seqstack,*stack;
//队列元素结构体
typedef struct node1
{
BiTree tree;
struct node1 *next;
} Qnode;
//队列的队头和队尾元素指针
typedef struct
{
Qnode *front;
Qnode *rear;
}LQnode;
//用于统计每一层叶子节点个数
typedef struct
{
int countleaf[10];
int countpoint[10];
int depth;
}countPoint;
/*typedef struct
{
char mid[100];
char post[100];
}tree; */
countPoint point;
//用于统计节点数的全局变量
int count1=0,count2=0;
//用于寻根函数
BiTree tree[100];
int i=0;
//tree list;//定义存储树序列的全局变量
void main_menu(BiTree root);//界面设置函数
stack init_seq();//初始化空栈,创建站顶元素,返回栈顶指针
int isempty(stack sq);//置栈空
void push(stack sq,BiTree tr);//进栈
void pop(stack sq,BiTree *p);//出栈
BiTree top(stack sq);//取栈顶数据
LQnode *init_LQnode();
int isempty_L(LQnode *q);
void in_LQnode(LQnode *q,BiTree tr);
void out_LQnode(LQnode *q,BiTree *tr);
void creat_Btree(BiTree *root,FILE *fp);//创建树
void pre_visit(BiTree root);//非递归先序遍历
void re_pro_visit(BiTree root);//递归先序遍历
void mid_visit(BiTree root);//非递归中序遍历
void re_mid_visit(BiTree root);//递归中序遍历
void post_visit(BiTree root);//非递归先后序遍历
void re_post_visit(BiTree root);//递归先后序遍历
void leval_visit(BiTree root);//层次遍历
BiTree parent (BiTree root,BiTree leaf);//搜索双亲函数
void print_path(BiTree root);//打印路径函数
void swap_tree(BiTree root);//交换左右子树
void post_visit_point(BiTree root);//递归统计有两个孩子节点和至少有一个孩子的节点,间接统计只有一个孩子的节点
int mid_visit_leaf(BiTree root);//输出叶子节点个数和叶子节点
void pro_visit_leaf(BiTree root);//先序统计叶子节点
int postTreeDepth(BiTree root);//求树的深度
void printTree(BiTree root,int h);//打印树
void count_leaf_Level(BiTree root,int k);//某一层k的叶子结点个数(待修改)
void print_count_leaf(BiTree root); //统计每一层的叶子节点个数
int Lush_degree(BiTree root);//二叉树的繁茂度
int IsComBinTree(BiTree root);//判定是否为完全二叉树
FILE * file();
void visit(char ch);
int main ()
{
system("title 树操作系统 ");
// int leaf,depth;//叶子节点数和树的深度
FILE *fp;
BiTree root;
fp= file();
creat_Btree(&root,fp);//创建树
point.depth=postTreeDepth(root);
main_menu(root);
return 0;
}
/**********************界面操作*********************/
void main_menu(BiTree root)
{
char ch[16];
int choice;
loop:
system("cls");
printf("\n\n\n\n");
printf("\n\t\t************欢迎进入树操作系统***********\n");
printf("\t\t \n");
printf("\t\t\t 1、遍历树\n");
printf("\t\t\t 2、输出叶子节点个数和叶子节点\n");
printf("\t\t\t 3、打印该二叉树中根节点到叶子节点的路径 \n");
printf("\t\t\t 4、树的深度 \n");
printf("\t\t\t 5、统计每一层的叶子节点个数 \n");
printf("\t\t\t 6、判定是否为完全二叉树 \n");
printf("\t\t\t 7、二叉树的繁茂度 \n");
printf("\t\t\t 8、打印该二叉树 \n");
printf("\t\t\t 9、交换左右子树\n");
printf("\t\t\t 0、退出 \n");
printf("\t\t\t\t(温馨提示:使用7功能前请先运行6,\n\t\t\t\t\t否则会造成运行结果存在偏差!)\n");
printf("\n\t\t************谢谢使用树操作系统***********\n");
InputBox(ch, 100, "请输入您的选择" );
sscanf(ch,"%d",&choice);
switch(choice)
{
case 1:{
system("cls");
printf("\n\n\n\n");
printf("\n\t\t************欢迎进入树操作系统***********\n");
printf("\t\t \n");
printf("\t\t\t 1、层次遍历\n");
printf("\t\t\t ");
leval_visit(root);
printf("\n");
printf("\t\t\t 2、非递归先序遍历\n");
printf("\t\t\t ");
pre_visit(root);
printf("\n");
printf("\t\t\t 3、递归先序遍历\n");
printf("\t\t\t ");
re_pro_visit(root);
printf("\n");
printf("\t\t\t 4、非递归中序遍历 \n");
printf("\t\t\t ");
mid_visit(root);
printf("\n");
printf("\t\t\t 5、递归中序遍历 \n");
printf("\t\t\t ");
re_mid_visit(root);
printf("\n");
printf("\t\t\t 6、非递归后序遍历 \n");
printf("\t\t\t ");
post_visit(root);
printf("\n");
printf("\t\t\t 7、递归后序遍历 \n");
printf("\t\t\t ");
re_post_visit(root);
printf("\n");
printf("\n\t\t************谢谢使用树操作系统***********\n");
printf("\t\t\t按任意键继续。。。。。。\n");
getch();
goto loop;
}
case 9:{printf("\n****************************************************\n");
printf("原树的先序序列\n");
pre_visit(root);
printf("\n");
swap_tree(root);
printf("交换后的先序序列\n");
pre_visit(root);
printf("\t\t\t按任意键继续。。。。。。\n");
getch();
goto loop;
}
case 2:{printf("\n****************************************************\n");
printf("该树的叶子节点总数为%d\n",mid_visit_leaf(root));
printf("\t\t\t按任意键继续。。。。。。\n");
getch();
goto loop;
}
case 4:{printf("\n****************************************************\n");
printf("该树的高度为%d\n",postTreeDepth(root));
printf("\t\t\t按任意键继续。。。。。。\n");
getch();
goto loop;
}
case 5:{printf("\n****************************************************\n");
printf("每一层的节点数和叶子节点数分别为:\n");
for(int j=1;j<=point.depth;j++)
{
count_leaf_Level(root,j);
printf("第%d层有%d个节点%d个叶子节点\n",j,point.countpoint[j],point.countleaf[j]);
}
printf("\t\t\t按任意键继续。。。。。。\n");
getch();
goto loop;
}
case 6:{printf("\n****************************************************\n");
printf("下面进行完全二叉树判断\n");
IsComBinTree(root);
printf("\t\t\t按任意键继续。。。。。。\n");
getch();
goto loop;
}
case 7:{
printf("\n****************************************************\n");
printf("二叉树的繁茂度为:%d\n",Lush_degree(root));
printf("\t\t\t按任意键继续。。。。。。\n");
getch();
goto loop;
}
case 8:
{
printf("\n****************************************************\n");
printf("打印二叉树:\n");
printTree(root,point.depth);
printf("\t\t\t按任意键继续。。。。。。\n");
getch();
goto loop;
}
case 3: {
printf("\n****************************************************\n");
printf("打印二叉树中叶子节点到根节点的路径:\n");
print_path(root);
printf("\t\t\t按任意键继续。。。。。。\n");
getch();
goto loop;
}
case 0:{printf("\n\n\t\t\t\t\t小七设计,谢谢使用!\n");
return ;
}
}
if(choice>9||choice<0)
{
printf("\t\t输入有误,请按任意键开启重新输入。。。。。。\n");
getch();
goto loop;
}
}
/********************栈操作 ***********************/
//初始化空栈,创建站顶元素,返回栈顶指针
stack init_seq()
{
stack sq;
sq=(stack)malloc(sizeof(seqstack));
sq->next=NULL;
return sq;
}
//置栈空
int isempty(stack sq)
{
if(sq->next==NULL)
return 1;
return 0;
}
//入栈函数
void push(stack sq,BiTree tr)
{
stack q;
q=(stack)malloc(sizeof(seqstack));
q->tree=tr;
q->next=sq->next;
sq->next=q;
// free(q);
}
//出栈函数
void pop(stack sq,BiTree *p)
{
// char *ch;
stack q;
q=sq->next;
sq->next=q->next;
(*p)=q->tree;
free(q);
}
//取栈顶元素
BiTree top(stack sq)
{
BiTree p;
if(!isempty(sq))
{
p=sq->next->tree;
}
return p;
}
/**********************队列操作*******************/
//初始化队列
LQnode *init_LQnode()
{
LQnode *q;
Qnode *p;
q=(LQnode*)malloc(sizeof(LQnode));
p=(Qnode*)malloc(sizeof(Qnode));
p->next=NULL;
q->front=q->rear=p;
return q;
}
int isempty_L(LQnode *q)
{
if(q->front==q->rear)
return 1;
else
return 0;
}
//入队
void in_LQnode(LQnode *q,BiTree tr)
{
Qnode *p;
p=(Qnode*)malloc(sizeof(Qnode));
p->tree=tr;
p->next=NULL;
q->rear->next=p;
q->rear=p;
}
//出队
void out_LQnode(LQnode *q,BiTree *tr)
{
if(!isempty_L(q))
{
Qnode *p;
p=(Qnode*)malloc(sizeof(Qnode));
p=q->front->next;
q->front->next=p->next;
*tr=p->tree;
free(p);
if(q->front->next==NULL)
q->rear=q->front;
}
}
/****************文件操作********************/
//打开文件操作
FILE * file()
{
FILE *fp;
char filename[]="树.txt";
fp=fopen(filename,"r");
if(fp==NULL)
{
printf("\n 打开文件失败,%s可能不存在,请先到对应文件夹下建立该文件!\n",filename);
exit(1);
}
return fp;
}
/********************二叉树操作**********************/
//扩展先序建立二叉树
//递归一次便给当前节点的数据域赋值,然后利用递归
//一次给该结点的左右子树赋值,实现二叉树的创建
void creat_Btree(BiTree *root,FILE *fp)
{
char ch;
ch=fgetc(fp);
if(ch==EOF)
return ;
if(ch=='#')
(*root)=NULL;
else{
(*root)=(BiTree)malloc(sizeof(BiTNode));
(*root)->data=ch;
creat_Btree(&((*root)->Lchild),fp);
creat_Btree(&((*root)->Rchild),fp);
}
}
//利用中序后序遍历建立二叉树
void creat_mid_post_tree(BiTree *root)
{
}
//非递归先序遍历
/* 首先对根节点和左子树以此访问并且顺序入栈,如果当前访问节点的左子树为空,
将该节点A退栈,访问该子树的右子树,对该节点的右子树按照上述方法进行遍历访问,访问完之后退回到,
A节点的双亲节点,将其退栈,同样的方法访问其右子树,以此类推访问完整个二叉树。
*/
void pre_visit(BiTree root)
{
stack s;
BiTree p;
s=init_seq();
p=root;
while(p!=NULL||!isempty(s))
{
while(p!=NULL)
{
visit(p->data);
push(s,p);
p=p->Lchild;
}
if(!isempty(s))
{
pop(s,&p);
p=p->Rchild;
}
}
}
//递归实现先序遍历
void re_pro_visit(BiTree root)
{
if(root)
{
visit(root->data);
re_pro_visit(root->Lchild);
re_pro_visit(root->Rchild);
}
}
//非递归中序遍历
/* 首先通过循环不断将节点入栈,直到找到左子树的最左侧的节点,从该节点进行遍历,先访问该结点,然后退栈,访问根节点,
再然后进入该根节点的右子树,同样的方法进行访问,访问完之后,将该根节点的根节点退栈,同样的方法访问他的右子树,一直循环直至
栈为空且,辅助指针为空,表示二叉树访问完
*/
void mid_visit(BiTree root)
{
stack s;
BiTree p;
s=init_seq();
p=root;
while(p!=NULL||!isempty(s))
{
while(p!=NULL)
{
push(s,p);
p=p->Lchild;
}
if(!isempty(s))
{
pop(s,&p);
visit(p->data);
p=p->Rchild;
}
}
}
//递归实现中序遍历
void re_mid_visit(BiTree root)
{
if(root)
{
re_mid_visit(root->Lchild);
visit(root->data);
re_mid_visit(root->Rchild);
}
}
//非递归后序遍历
/* 首先通过循环不断将节点入栈,直到找到左子树的最左侧的节点,然后取栈顶元素,即该结点,及对其右子树进行考察,
如果其右子树是空或者是已经访问过,则退栈,访问站顶元素,并将其地址赋值给第二辅助标记指针变量,并将第一指
针变量置为空,便于再退栈,访问下一个节点的数据,否则如果该节点的右子树不为空且未被访问过,则同样的访问该节点的右子树。
*/
void post_visit(BiTree root)
{
stack s;
s=init_seq();
BiTree p,q;
p=root;q=NULL;
while(!isempty(s)||p!=NULL)
{
while(p!=NULL)
{
push(s,p);
p=p->Lchild;
}
if(!isempty(s))
{
p=top(s);
if((p->Rchild==NULL)||(p->Rchild==q))
{
pop(s,&p);
visit(p->data);
q=p;
p=NULL;
}
else
p=p->Rchild;
}
}
}
//递归实现后序遍历
void re_post_visit(BiTree root)
{
if(root)
{
re_post_visit(root->Lchild);
re_post_visit(root->Rchild);
visit(root->data);
}
}
//层次遍历
void leval_visit(BiTree root)
{
LQnode *q;
q=init_LQnode();
BiTree p;
in_LQnode(q,root);
while(!isempty_L(q))
{
out_LQnode(q,&p);
visit(p->data);
if(p->Lchild!=NULL)
in_LQnode(q,p->Lchild);
if(p->Rchild!=NULL)
in_LQnode(q,p->Rchild);
}
}
//搜索某一节点的双亲
BiTree parent (BiTree root,BiTree leaf)
{
BiTree p;
if(root==NULL)
return NULL;
if(root->Lchild==leaf||root->Rchild==leaf)
return root;
p=parent(root->Lchild,leaf);
if(p!=NULL)
return p;
else
return (parent(root->Rchild,leaf));
}
//打印某一节点到根节点的路径
void print_path(BiTree root)
{ BiTree p;
char ch[100];
int k;
mid_visit_leaf(root);
for(int j=0;j { k=0; p=tree[j]; printf("\n"); printf("%c:",p->data); // visit(p->data); while(p->data!=root->data) { p=parent (root,p); ch[k]=p->data; k++; } while(k>=1) { visit(ch[k-1]); k--; }//printf("\n"); } } //交换左右子树 /*通过递归实现,原理就是将换两个变量的值*/ void swap_tree(BiTree root) { BiTree p; p=root->Lchild; root->Lchild=root->Rchild; root->Rchild=p; if(root->Lchild!=NULL) swap_tree(root->Lchild); if(root->Rchild!=NULL) swap_tree(root->Rchild); } //递归统计有两个孩子节点和至少有一个孩子的节点,间接统计只有一个孩子的节点 void post_visit_point(BiTree root) { if(root) { if(root->Lchild!=NULL&&root->Rchild!=NULL) count2++;//统计有两个孩子的节点个数 if((root->Lchild!=NULL||root->Rchild!=NULL)) count1++;//统计至少有一个孩子的节点个数 post_visit_point(root->Lchild); post_visit_point(root->Rchild); } } //输出叶子节点个数和叶子节点 int mid_visit_leaf(BiTree root) { int leaf1=0,leaf2=0; if(root) { if(root->Lchild==NULL&&root->Rchild==NULL) { tree[i]=root; i++; visit(root->data); return 1; } leaf1=mid_visit_leaf(root->Lchild); leaf2=mid_visit_leaf(root->Rchild); } return (leaf1+leaf2); } //求树的深度 int postTreeDepth(BiTree root) { int hr,hl,h; if(root==NULL) return 0; else { hl=postTreeDepth(root->Lchild); hr=postTreeDepth(root->Rchild); h=((hr>hl)?hr:hl)+1; return h; } } //打印树 (参数分别是树根和树的深度) void printTree(BiTree root,int h) { if(root==NULL) return ; printTree(root->Rchild,h+1); for(int j=0;j { printf("-"); } printf("%c\n",root->data); printTree(root->Lchild,h+1); } //某一层k的叶子结点个数(待修改)并记录树的深度 void count_leaf_Level(BiTree root,int k) { BiTree QCountPoint[100]; BiTree bt; bt=root; int front,rear; int last,level; front=rear=0; if(bt==NULL||k<1) return ; rear++; QCountPoint[rear]=bt; last=rear; level=1; while(rear!=front) { front=front+1; bt=QCountPoint[front]; if(level==k&&bt->Lchild==NULL&&bt->Rchild==NULL) point.countleaf[k]++; if(level==k) point.countpoint[k]++; if(bt->Lchild!=NULL) { rear=rear+1; QCountPoint[rear]=bt->Lchild; } if(bt->Rchild!=NULL) { rear=rear+1; QCountPoint[rear]=bt->Rchild; } if(front==last) { level++; last=rear; } if(level>k) return ; } } //二叉树的繁茂度 int Lush_degree(BiTree root) { int max=0; for(int j=1;j { if(max max=point.countpoint[j]; } // return (max*postTreeDepth(root)); return (max*point.depth); } //判定是否为完全二叉树 int IsComBinTree(BiTree root) { int depthL,depthR,j; depthL=postTreeDepth(root->Lchild)+1; depthR=postTreeDepth(root->Rchild)+1; if((depthL==depthR)||(depthL-depthR==1)) { printf("满足条件一:对于任何节点,若其右子树的层高为k,则其左子树可能为k或者是k+1\n"); for( j=1;j<=point.depth-2;j++) { if(point.countleaf[j]!=0) break; } if(j==(point.depth-2)) { printf("满足条件二:有叶子节点只可能出现在最大的两层上\n"); return TRUE; } else { printf("不满足条件二:有叶子节点只可能出现在最大的两层上\n"); return FALSE; } } else{ printf("不满足条件一:对于任何节点,若其右子树的层高为k,则其左子树可能为k或者是k+1\n"); return FALSE; } } /************访问函数*****************/ void visit(char ch) { putchar(ch); printf(" "); }