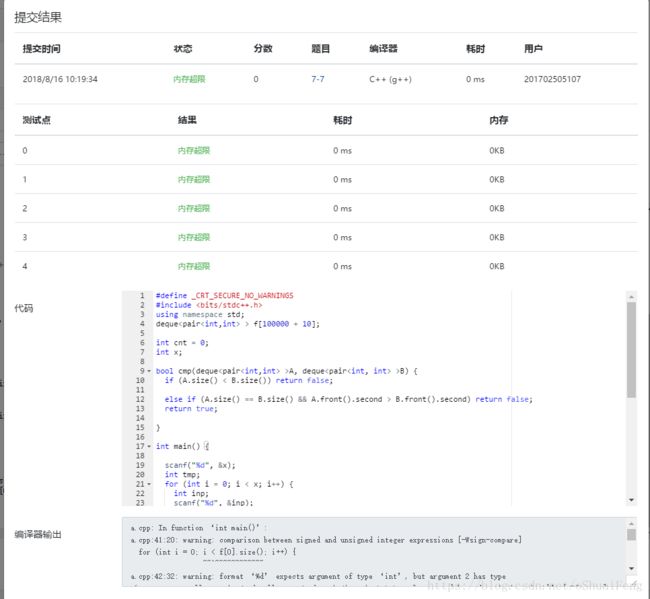
7-7 最长连续递增子序列(20 分) 普通STL解出
这道题我看了一下 决定写。 在写之前网上看到很多高手的题解,深表敬意。
只是我想用STL来完成一下这道题。
7-7 最长连续递增子序列(20 分)
给定一个顺序存储的线性表,请设计一个算法查找该线性表中最长的连续递增子序列。例如,(1,9,2,5,7,3,4,6,8,0)中最长的递增子序列为(3,4,6,8)。
输入格式:
输入第1行给出正整数n(≤105);第2行给出n个整数,其间以空格分隔。
输出格式:
在一行中输出第一次出现的最长连续递增子序列,数字之间用空格分隔,序列结尾不能有多余空格。
输入样例:
15
1 9 2 5 7 3 4 6 8 0 11 15 17 17 10
输出样例:
3 4 6 8
这次我要使用一个名叫 双端队列的东西 deque .
本次练习 共测试了几个样例
1 . 1 2 3 4 5
2. 5 4 3 2 1
3. 1 2 3 1 2 3 4
4. 5 4 3 2 1 2 3 4 5 6 6 7 8 9 10 9
5. 0
我的代码是怎样想出来的??
1.看到题目之后 我想 既然是一个递增子序列 我可以用 双端队列数组存储下这些数列 然后动用带cmp函数的sort排序输出双端队列数组的首地址下的所有元素。 比如题目样例 1 9 2 5 7 3 4 6 8 0 11 15 17 17 10 可想而知 1 9 存在 [0] ,2 5 7 存在 [1] , 3 4 6 8 存在 [2] , 0 11 15 17存在 [3] 17 存在 [4] 10 存在 [5] 这个时候题目有一个重要的 提示 “在一行中输出第一次出现的最长连续递增子序列”
什么!!第一次。这可难办了 因为数数的序列其实并不是有序的 那我在排序时候可想而知 我不知道谁才是第一子序列,自然会在这里栽跟头。这里当然有两种办法,第一种建一个标记数组 map
我选择了第二个 我把 deque 定义的时候修改为 deque
显然以上方法是不可取的 ,我们可以来欣赏一下shan上面完成的代码。 【内存超限 不可取】
#define _CRT_SECURE_NO_WARNINGS
#include
using namespace std;
deque > f[100000 + 10];
int cnt = 0;
int x;
bool cmp(deque >A, deque >B) {
if (A.size() < B.size()) return false;
else if (A.size() == B.size() && A.front().second > B.front().second) return false;
return true;
}
int main() {
scanf("%d", &x);
int tmp;
for (int i = 0; i < x; i++) {
int inp;
scanf("%d", &inp);
if (i == 0) {
tmp = inp;
f[cnt].push_back({inp,cnt});
}
else {
if (inp <= tmp) {
i = inp;
cnt++;
f[cnt].push_back({ inp,cnt });
}
else {
f[cnt].push_back({ inp,cnt });
}
}
tmp = inp;
}
sort(f, f + cnt, cmp);
for (int i = 0; i < f[0].size(); i++) {
i == 0 ? printf("%d", f[0][i]) : printf(" %d", f[0][i]);
}
system("pause");
return 0;
}
转折-- 双变量 爆破成功
难道 这就无解了吗 看看钟表 凌晨 2:45 分 算了 明天起来再说吧! 躺在床上睡不着,都说睡觉要在 24:00 -- 3:00 才有益。睡不着就会胡思乱想。想着想着 突然想到 不需要数组 不需要sort 只需要 两个 deque
·····早晨 8:00 :
拿出了题目想到了半夜的思路 就试了一下。
思路是这样的 :
1 . 定义两个 deque
2 .定义 临时变量B 存储上一次 输入的值。
2.1. 考虑到 临时变量B第一次要单独处理。
3.接着每次输入[除去第一次] 都用现输入的值和临时变量B相比较 如果比临时变量大则 更新临时变量B 同时把 输入的值放入临时变量A之中(尾插)
3.1.如果临时变量小于等于 输入的值 那么 判断临时变量A的 size()是不是 大于(没有等于,为什么见 3.2.)答案变量的size(),如果大了就更新,接着执行 临时变量A.clear(); 再把刚刚输入的值放入临时变量接着下一次循环。如果小了就不更新,接着执行 临时变量A.clear(); 再把刚刚输入的值放入临时变量接着下一次循环。
3.2. 没有等于源于 题目中 “在一行中输出第一次出现的最长连续递增子序列” 我们知道我们是从头往后去遍历的,那么
假定我们 前面已经得到一个长度为 5 的连续序列 那一定就是最先出现的长度为5的子序列 如果后面又出现 临时bian变量的序列长度为 5 那么 它就不可能代替答案序列 成为答案。因为以己有比它优先的长度为5的序列。
就是这样核心思路核心的代码出来了:
#define _CRT_SECURE_NO_WARNINGS
#include
using namespace std;
class firstq {
public:
deque f; // 答案变量
deque ftmp; // 临时变量A
int cnt = 0; // 第一次更新策略
int x; // 数据量
int F() {
scanf("%d", &x);
int tmp; // 临时变量B
for (int i = 0; i < x; i++) {
int inp;
scanf("%d", &inp);
if (i == 0) {
tmp = inp;
ftmp.push_back(inp);
}
else {
if (inp <= tmp) {
if (cnt == 0) f = ftmp; // 第一次更新策略使用地方
else if (cnt&&f.size() < ftmp.size()) f = ftmp;
cnt++; // 第一次更新策略唯一修改地方
ftmp.clear();
ftmp.push_back(inp);
}
else {
ftmp.push_back(inp);
}
}
tmp = inp;
}
if (f.size() < ftmp.size()) f = ftmp;
for (int i = 0; i < f.size(); i++) {
i == 0 ? printf("%d", f[i]) : printf(" %d", f[i]);
}
system("pause");
return 0;
}
};
int main() {
firstq A;
A.F();
}
PS.写CLASS主要是想和其他网上程序用对数器验证。
----来自海南,在山东
2018年8月16日