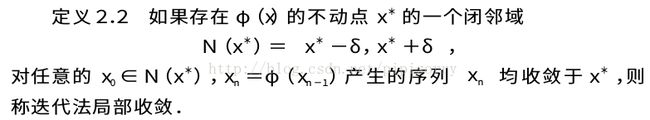最优化方法：非线性方程的求极值方法
http://blog.csdn.net/pipisorry/article/details/23553263
本文主要讲解 数值分析：非线性方程的求根方法，但是等价于最优化方法：非线性方程的求极值方法。
最优化方法
最优化方法是一种数学方法，它是研究在给定约束之下如何寻求某些因素(的量)，以使某一(或某些)指标达到最优的一些学科的总称。随着学习的深入，博主越来越发现最优化方法的重要性，学习和工作中遇到的大多问题都可以建模成一种最优化模型进行求解，比如我们现在学习的机器学习算法，大部分的机器学习算法的本质都是建立优化模型，通过最优化方法对目标函数（或损失函数）进行优化，从而训练出最好的模型。常见的最优化方法有梯度下降法、牛顿法和拟牛顿法、共轭梯度法等等。
凸函数
凸函数：优化理论中，设f是定义域为实数的函数，如果对于所有的实数x，
，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的（
），那么f是凸函数。如果
或者
，那么称f是严格凸函数。 当f是（严格）凹函数当且仅当-f是（严格）凸函数。比如
是凹函数。
零点
1 如果 x * 使 f( x * )=0,则称 x * 为方 程的根,或称为 函数f( x )的零点;
当 f( x )为多项式时,即
其中0<| g( x* )|<∞, m 为 正 整数,则称 x* 为 f(x )的 m 重零 点,当m=1时,称 x*为 f( x )的单重零点或单根.
这里我们要求解的就是非线性方程的解（即零点）x*。
Note: 如果我们将凸函数g(x)的导数g'(x)作为f(x)并求其零点，其实我们就是求g'(x)=0的零点，这样就是求出凸函数g(x)的极值点，这样就是解决了最优化问题了。
一般情况下,用计算机求解非线性方程步骤
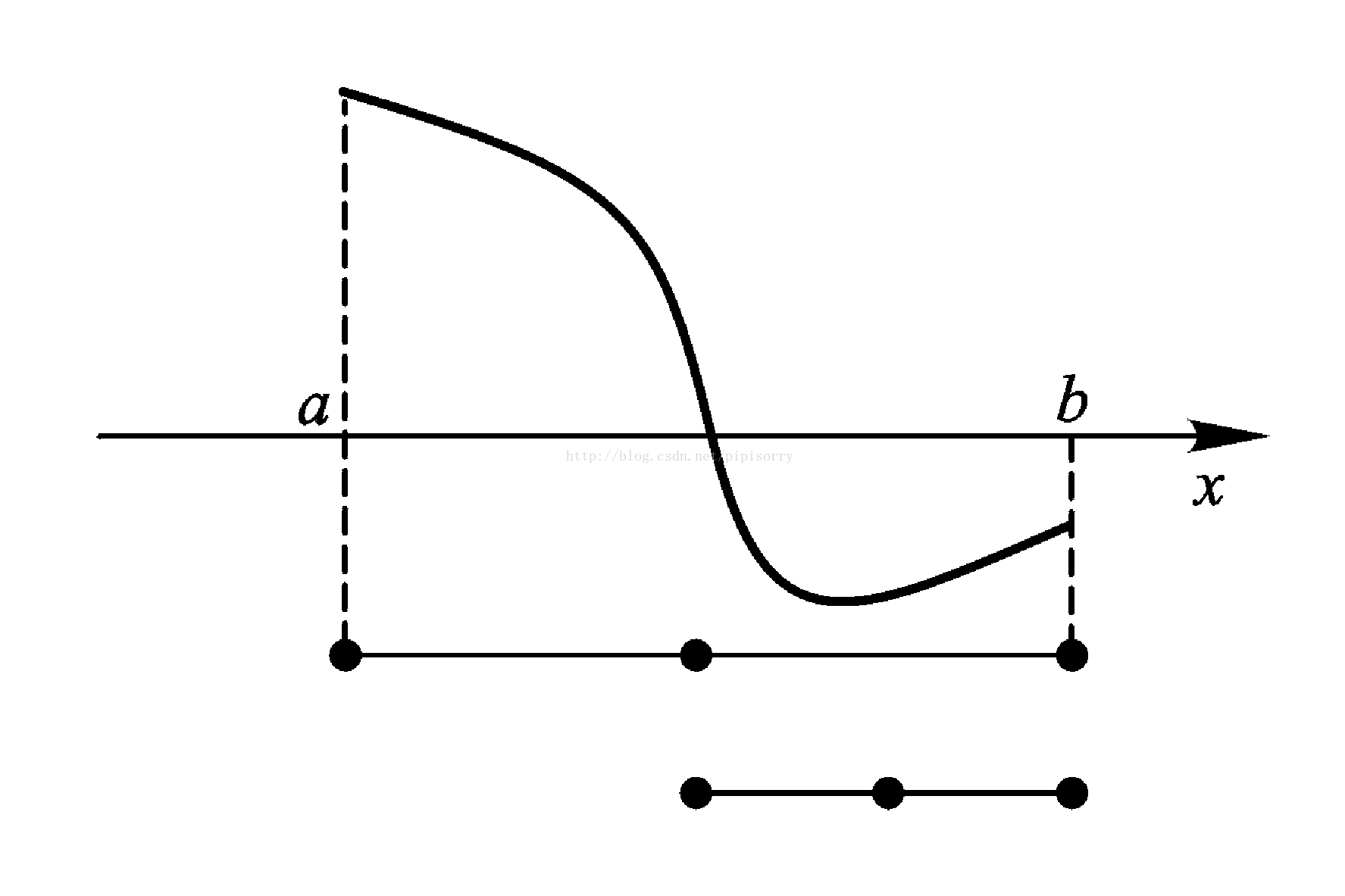
第一步:对方程 f( x )=0的根进行隔离.找出隔根 区间(区间内包含方程的一个根).
第二步:利用迭代法计算满足一 定精度的根近似值.在方程的隔根区间[a ,b]内从给定的一 个(或多个)出发值 x 0 ,按某种方法产生一个序列x 0 ,x 1 ,x 2 ,...,x n ,...此序列在某种条件下收敛于方 程的根 x * .
对高于4次的代数方程,不存在 通用的求根公式,而对超越方程一般很难直接求出其准确解,所 以,数值方 法就 是非 常实用 和有效的方法.
本博客主要介 绍非线性方程求根的逐次逼近法,同时也讨论方法的收敛性和误差估计等问题.
皮皮blog
二分法
又称实根对分法。二分法本质上是一种区间迭代算法,在迭代过程中不断对隔根区间进行压缩,以区间中点逼近方程的根.它所涉及的理论是连续函数介值定理.
连续函数介值定理
设函数f(x)在区间a,b上连续,且f(a)f(b)<0,则方程f(x)=0在区间(a,b)内至少有一个根.
二分法的基本思想
对有根区间a,b逐次分半,首先计算区间a,b的中间点x0,然后分析可能出现的三种情况:
如果f(x0)f(a)<0,则f(x)在区间a,x0内有零点;
如果f(x0)f(b)<0,则f(x)在区间x0,b内有零点;
如果f(x0)=0,则x0是f(x)在区间a,b内所求零点.
过程的细节如下:
取a,b为起始区间,取区间中点x0=1/2(a+b),计算f(x0).若f(x0)=0,则x0就是方程的解;若f(x0)f(a)<0,取a1=a,b1=x0;
若f(x0)f(b)<0,取a1=x0,b1=b. a1,b1的长度是区间a,b的一半.
对任意n>0,设第n个区间为an,bn, 取区间中点xn=1/2(an+bn),计算f(xn).若f(xn)=0,则xn是方程的解;若f(xn)f(an)<0,取an+1=an,bn+1=xn;若f(xn)f(bn)<0,取an+1=xn,bn+1=bn.所得区间 a n+ 1,bn+1的长度是an,bn的一半.
二分法所得区间套性质
二分法收敛定理
当n充分大时,取xn=(an+bn)/2为方程的解x*的近似值,有如下二分法收敛定理.
二分法解非线性方程算法
皮皮blog
迭代法
迭代法利用逐次逼近过程求解非线性方程(或方程组),同样的计算过程往往要多次进行,而每次都要以前一次计算结果代入计算.在迭代计算中,选取迭代初值、按迭代格式进行迭代计算以及判别收敛是迭代的三个主要部分.
对迭代法研究的主要内容包括:迭代格式的构造、迭代过程的收敛性、迭代收敛速度的估计以及加速收敛的技巧.
不动点迭代
将方程f(x)=0变换成等价的形式x=φ(x),如果有x*满足f(x*)=0,则x*也满足x*=φ(x*),反之亦然,此时称x*是函数φ(x)的一个不动点.求f(x)的零点等价于求φ(x)的不动点.
选择一个初始近似值x0,按照以下公式迭代计算
xn+1=φ(xn)(n=0,1,...,n),
称为不动点迭代法,它产生的序列xk如果收敛到x*就是φ(x)的不动点.
迭代过程的几何图形解释
基本思想是 ,将求 解隐式方程 f( x )=0 问题转化成计算一组显示的计算公式 x n+1 = φ (x n ).
f(x)=0变换为x=φ(x)的途径
可以通过不同的途径将方程f(x)=0变换为x=φ(x).例如,令φ(x)=x-f(x),也可以用其他更复杂的方法.原方程化为不同迭代格式时,有的迭代收敛,有的发散.收敛时,收敛的速度也有所不同.因此,用迭代法求方程f(x)=0近似解时,如何构造迭代函数φ(x),φ(x)满足什么条件能保证迭代收敛是必须研究的问题.
不动点迭代法的收敛性
不动点存在性及唯一性引理
在 a ,b 上函数 φ( x )不动点的存在性,给出不动点存在唯一的充分条件
不动点迭代法的全局收敛性
不动点迭代法收敛的一个充分条件
迭代精度及迭代结束控制
式(2.4)不仅可以用来估计迭代n次时的误差,还可以用来估计达到给定的精度要求ε所需的迭代次数.如果欲使x*-xn<ε,只须
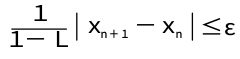成立即可.注意到估计式(2.5),当L越小时,序列{xn}收敛越快.式(2.4)表明只要相邻两次迭代的偏差足够小,就可以保证近似解xn有足够的精度.因此算法设计中,常用条件|xn-xn-1|≤ε来控制迭代过程结束。
当|xn|的数量级较大时,也可以用相对误差
作为迭代终止的条件;为避免出现无限制地迭代,还可规定一个最大的迭代次数.
实际上L不易求得,而且对大范围的有根区间a,b,定理2.4的条件(1)不一定成立.因此,利用定理2.4分析迭代法在区间a,b上的收敛性比较困难.
不动点迭代法的局部收敛性和收敛阶
该定理表明,只要构造迭代函数φ(x),使其在所求根x*的邻域满足导数绝对值小于1,即可保证迭代法收敛.
Note: 梯度下降就是不动点迭代的一种特殊情况：x = x - f'(x) = φ(x), 凸函数领域中应该可以保证0 < f''(x) < 2，则|φ‘(x)| = |1 - f''(x)| < 1,故梯度下降可以保证迭代收敛。
[最优化方法：梯度下降（批梯度下降和随机梯度下降）]
事实上,在用不动点迭代法时,常常先用二分法求得较好的初值,然后进行迭代.
收敛阶
显然,收敛阶r刻画了序列{xn}的收敛速度,r愈大收敛越快.特别地,当r=1,称序列是线性收敛的;若r>1,称为超线性收敛;r=2为平方收敛.
高阶收敛定理
不动点迭代法的加速
有时迭代过程收敛缓慢而使计算量很大。
from: http://blog.csdn.net/pipisorry/article/details/23553263
ref: [不动点迭代和优化方法]
[[[Math] 常见的几种最优化方法]]
[最优化/Optimization文章合集]**