《剑指offer》Java学习录:树(面试题6:重建二叉树)
文章目录
- 树
- 树的定义
- 二叉树
- 二叉树实现(Java/C++)
- Java实现
- C++实现
- 二叉树的遍历
- 深度优先搜索(Depth-First Search)
- 前序遍历
- 中序遍历
- 后续遍历
- 广度优先搜索(Breadth-First Search)
- 二叉搜索树
- 新增节点
- 搜索
- 删除
- 面试题 6:重建二叉树
- 题目
- 分析
- 解:Java
- 解:C++
树
在数据结构中,我们把存在逻辑上的起点和终点的数据结构,成为线性的数据结构。例如链表、栈和队列等都是线性的数据结构。
树是众所周知的非线性数据结构。它在逻辑上没有终点,且不以线性方式存储数据。他们按层次组织数据。
树的定义
树(tree) 是被称为 结点(node)实体的集合。结点通过边(edge)连接。每个结点都包含值或数据(value/date),并且每个结节点可能有子结点,也可能没有。
树的首结点叫根结点(即root结点)。如果这个根结点和其他结点所连接,那么根结点是父结点(parent node),与根结点连接的是子结点(child node)。
所有的结点都通过边(edge)连接,它负责管理节点之间的逻辑关系。
叶子结点(leaves)是树末端,它们没有子结点。
树的高度(height)和深度(depth):
- 树的高度是到叶子结点(树末端)的长度
- 结点的深度是它到根结点的长度
二叉树
二叉树是树结构中特殊且常用的类型,每个节点最多有两个子节点,被称作左孩子和右孩子(你可以叫做左节点和右节点)。
二叉树实现(Java/C++)
在实现二叉树时,我们只需要注意,一个节点中有三个属性:数据、左节点、右节点。
Java实现
public class BinaryTree {
public BinaryTree left;
public BinaryTree right;
public String value;
public BinaryTree(BinaryTree left, BinaryTree right, String value) {
this.left = left;
this.right = right;
this.value = value;
}
public BinaryTree(String value) {
this(null, null, value);
}
/**
* 将给定的新左节点值插入到当前节点中:
* 1. 如果当前节点没有左节点,新节点为当前节点的左节点。
* 2. 如果当前节点有左节点,新节点为当前节点的左节点,原左节点作为新节点的左节点。
*
* @param currentNode 插入左节点的父节点,即当前节点
* @param value 新左节点的值
*/
public void insertLeft(BinaryTree currentNode, String value) {
if (currentNode == null) {
return;
}
BinaryTree newLeftNode = new BinaryTree(value);
if (currentNode.left != null) {
BinaryTree leftNode = currentNode.left;
newLeftNode.left = leftNode;
}
currentNode.left = newLeftNode;
}
public void insertRight(BinaryTree currentNode, String value) {
if (currentNode == null) {
return;
}
BinaryTree newLeftNode = new BinaryTree(value);
if (currentNode.right != null) {
BinaryTree leftNode = currentNode.right;
newLeftNode.right = leftNode;
}
currentNode.right = newLeftNode;
}
}
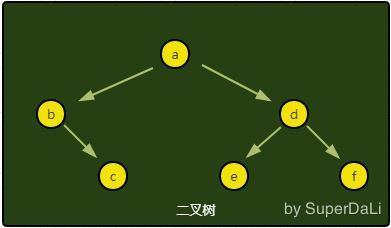
我们可以利用BinaryTree来构造一个二叉树:
public class Main {
public static void main(String args[]) {
BinaryTree node_a = new BinaryTree("a");
node_a.insertLeft(node_a, "b");
node_a.insertRight(node_a, "c");
BinaryTree node_b = node_a.left;
node_b.insertRight(node_b, "d");
BinaryTree node_c = node_a.right;
node_c.insertLeft(node_c, "e");
node_c.insertRight(node_c, "f");
}
}
C++实现
二叉树的遍历
树的遍历有两种方式,深度优先搜索(DFS)和广度优先搜索(BFS)。
在Wikipedia中,被描述如下:
DFS是用来遍历或搜索树数据结构的算法。从根节点开始,在回溯之前沿着每一个分支尽可能远的探索。
BFS是用来遍历或搜索树数据结构的算法。从根节点开始,在探索下一层邻居节点前,首先探索同一层的邻居节点。
深度优先搜索(Depth-First Search)
DFS从根节点开始,在回溯之前沿着每一个分支尽可能远的探索。
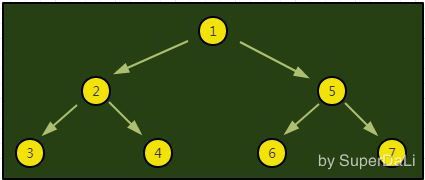
如上图所示二叉树,按照DFS的方式遍历,输出顺序为:1-2-3-4-5-6-7。
具体的遍历步骤如下:
- 从根结点(1)开始。输出
- 进入左结点(2)。输出
- 然后进入左孩子(3)。输出
- 回溯,并进入右孩子(4)。输出
- 回溯到根结点,然后进入其右孩子(5)。输出
- 进入左孩子(6)。输出
- 回溯,并进入右孩子(7)。输出
- 完成
当我们深入到叶结点时回溯,这就被称为 DFS 算法。 根据根节点输出顺序的不同,又被分为前序遍历、中序遍历、后序遍历。
前序遍历
前序遍历是在DFS的基础上,按照以下步骤输出节点:
- 输出当前节点值。
- 如果有左子节点,进入该节点,输出左子节点值。
- 如果有右子节点,进入该节点,输出右子节点值。
简而言之,节点的输出顺序为:当前节点-左子节点-右子节点
代码如下:
/**
* 前序遍历
*
* @param node 二叉树的节点
*/
public static void preOrder(BinaryTree node) {
if (node != null) {
System.out.println(node.value);
if (node.left != null) {
node.left.preOrder(node.left);
}
if (node.right != null) {
node.right.preOrder(node.right);
}
}
}
对于,如图所示的二叉树:

前序遍历的输出结果为:1-2-3-4-5-6-7
调试代码如下:
public class Main {
public static void main(String args[]) {
BinaryTree node_1 = new BinaryTree("1");
node_1.insertLeft(node_1, "2");
node_1.insertRight(node_1, "5");
BinaryTree node_2 = node_1.left;
node_2.insertLeft(node_2, "3");
node_2.insertRight(node_2, "4");
BinaryTree node_5 = node_1.right;
node_5.insertLeft(node_5, "6");
node_5.insertRight(node_5, "7");
BinaryTree.preOrder(node_1);
}
}
中序遍历
和前序遍历类似,中序遍历只是将左子节点和当前节点输出顺序互换,也就是:左子节点-当前节点-右子节点。
遍历输出代码如下:
/**
* 中序遍历
*
* @param node 二叉树的节点
*/
public static void inOrder(BinaryTree node) {
if (node != null) {
if (node.left != null) {
node.left.inOrder(node.left);
}
System.out.println(node.value);
if (node.right != null) {
node.right.inOrder(node.right);
}
}
}
中序遍历的输出结果为:3-2-4-1-5-5-7
调试代码和前序遍历调试代码类似,只是将遍历调用改为:BinaryTree.inOrder(node_1);即可。
后续遍历
同样,后序遍历的输出顺序是:左子节点-右子节点-当前节点。
遍历输出代码如下:
/**
* 后序遍历
*
* @param node 二叉树的节点
*/
public static void postOrder(BinaryTree node) {
if (node != null) {
if (node.left != null) {
node.left.postOrder(node.left);
}
if (node.right != null) {
node.right.postOrder(node.right);
}
System.out.println(node.value);
}
}
后序遍历的输出结果为:3-4-2-6-7-5-1
调试代码和前序遍历调试代码类似,只是将遍历调用改为:BinaryTree.postOrder(node_1);即可。
篇幅有限,就不再列出C++的相关实现了,都差不多。
广度优先搜索(Breadth-First Search)
- 0层:只有节点(1)
- 1层:有节点(2)和(5)
- 2层:有节点(3)、(4)、(6)、(7)
BFS算法,就是先遍历输出第一层,再遍历并从左到右输出第二层,接着第三层……
要实现算法,我们需要一个先入先出的模型-队列。实现步骤如下:
- 将节点(1)入队。
- 从队列中取出一个节点输出,并将它的所有子节点从左到右依次入队。
- 重复步骤#2,直到队列中没有节点。
代码如下:
/**
* 广度优先搜索
*
* @param node 二叉树的节点
*/
public static void bfsOrder(BinaryTree node) {
if (node == null) {
return;
}
Queue<BinaryTree> queue = new ArrayDeque<>();
queue.add(node);
while (!queue.isEmpty()) {
BinaryTree currentNode = queue.poll();
System.out.println(currentNode.value);
if (currentNode.left != null) {
queue.add(currentNode.left);
}
if (currentNode.right != null) {
queue.add(currentNode.right);
}
}
}
后序遍历的输出结果为:1-2-5-3-4-6-7
调试代码和前序遍历调试代码类似,只是将遍历调用改为:BinaryTree.bfsOrder(node_1);即可。
二叉搜索树
二叉搜索树又称为二叉排序树或二叉有序数。它的逻辑结构是有序的,特点是:一个节点的值大于其左节点,小于右节点。
这样的特征让二叉搜索树的查找可以适用于折半查找原理。
二叉搜索树中的添加节点将不可以手动指定新增节点是插入左节点还是右节点了。新增的节点是当前节点的左节点还是右节点将根据规则决定。
新增节点
下面是二叉搜索树新增节点的例子:
/**
* 二叉搜索树插入新节点
*
* @param node 当前树,注意必须是二叉搜索树,新增节点后可能是二叉搜索树
* @param value 新节点的值
*/
public void insertNode(BinaryTree node, int value) {
if (node == null) {
return;
}
if (value <= Integer.valueOf(node.value) && node.left != null) {
node.left.insertNode(node.left, value);
} else if (value <= Integer.valueOf(node.value)) {
node.left = new BinaryTree(String.valueOf(value));
} else if (value > Integer.valueOf(node.value) && node.right != null) {
node.right.insertNode(node.right, value);
} else {
node.right = new BinaryTree(String.valueOf(value));
}
}
用文字描述就是:
- 如果当前节点值大于或等于新节点值,新节点应该放置在当前节点的左子树中。
- 如果当前节点左子树为null,则新节点成为当前节点的左节点。如果当前节点左子树不为null,递归#1#2。
- 如果当前节点值小于新节点值,新节点应该放置在当前节点的右子树中。
- 如果当前节点右子树为null,则新节点成为当前节点的右节点。如果当前节点右子树不为null,递归#3#4。
搜索
二叉搜索树因为是有序,所以它的遍历搜索将变得简单。步骤如下:
- 从根节点开始,给定值小于当前节点值吗?
- 如果小于,接下来进入左子树遍历查找,如果大于将进入右子树查找。
- 如果相等,恭喜你,你找到了给定值。
代码如下:
/**
* 二叉搜索树查找节点是否存在
*
* @param node
* @param value
* @return
*/
public boolean findNode(BinaryTree node, int value) {
if (node == null) {
return false;
}
if (value < Integer.valueOf(node.value) && node.left != null) {
return node.left.findNode(node.left, value);
}
if (value > Integer.valueOf(node.value) && node.right != null) {
return node.right.findNode(node.right, value);
}
return value == Integer.valueOf(node.value);
}
删除
二叉搜索树中,比较复杂的算法是删除指定节点。它需要考虑三种情况,1、删除的节点没有子节点,2、删除的节点只有一个节点,3、删除的节点有两个节点。
第一种情况:没有子节点
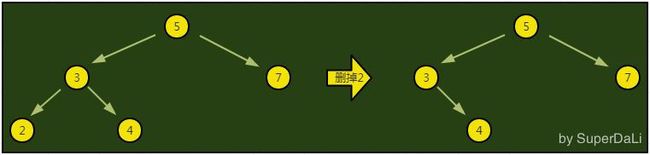
这是最简单的一种情况,直接删除就好。
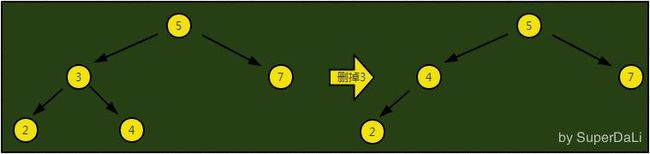
这种情况需要做两步操作:
- 删除指定节点。
- 将删除节点的子节点替换被删节点的位置。
这是最复杂的一种情况,当节点有两个子节点时,需要从该节点的右子树开始,找到具有最小值的节点。用这个节点替换掉被删除节点的位置。
代码如下:
/**
* 二叉搜索树删除节点
*
* @param node 当前节点
* @param value 指定被删除节点的值
* @param parent 当前节点父节点
* @return 成功返回true 失败返回false
*/
public boolean removeNode(BinaryTree node, Integer value, BinaryTree parent) {
if (node != null) {
if (value < Integer.valueOf(node.value) && node.left != null) {
return node.left.removeNode(node.left, value, node);
} else if (value < Integer.valueOf(node.value)) {
return false;
} else if (value > Integer.valueOf(node.value) && node.right != null) {
return node.right.removeNode(node.right, value, node);
} else if (value > Integer.valueOf(node.value)) {
return false;
} else {
if (node.left == null && node.right == null && node == parent.left) {
parent.left = null;
node.clearNode(node);
} else if (node.left == null && node.right == null && node == parent.right) {
parent.right = null;
node.clearNode(node);
} else if (node.left != null && node.right == null && node == parent.left) {
parent.left = node.left;
node.clearNode(node);
} else if (node.left != null && node.right == null && node == parent.right) {
parent.right = node.left;
node.clearNode(node);
} else if (node.right != null && node.left == null && node == parent.left) {
parent.left = node.right;
node.clearNode(node);
} else if (node.right != null && node.left == null && node == parent.right) {
parent.right = node.right;
node.clearNode(node);
} else {
node.value = String.valueOf(node.right.findMinValue(node.right));
node.right.removeNode(node.right, Integer.valueOf(node.right.value), node);
}
return true;
}
}
return false;
}
/**
* 查找二叉搜索树中的最小值坐在的节点
*
* @param node 二叉搜索树节点
* @return 返回node树中,最小值所在的节点
*/
public Integer findMinValue(BinaryTree node) {
if (node != null) {
if (node.left != null) {
return node.left.findMinValue(node.left);
} else {
return Integer.valueOf(node.value);
}
}
return null;
}
/**
* 清空n节点
*
* @param node 需要被清空的节点
*/
public void clearNode(BinaryTree node) {
node.value = null;
node.left = null;
node.right = null;
}
面试题 6:重建二叉树
题目
输入某二叉树的前序遍历和终须遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如,输入前序遍历序列{1, 2, 4, 7, 3, 5, 6, 8}和中序遍历序列{4, 7, 2, 1, 5, 3, 8, 6},则重建出如下图所示二叉树并输出它的头结点。

二叉树节点的定义如下:
struct BinaryTreeNode {
int m_nValue;
BinaryTreeNode *m_pLeft;
BinaryTreeNode *m_pRight;
};
分析
在二叉树的前序遍历序列中,第一个数字是树的根节点。单在中序遍历序列中,根节点在序列的中间,左子树位于根节点的左边,右子树位于根节点右边。
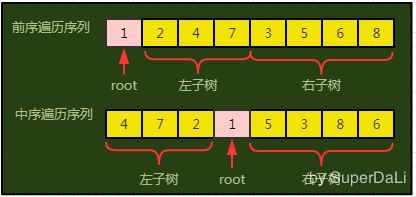
如图,中序遍历序列中,有3个数字是左子树节点的值,因此左子树总共有3个左子节点。所以,我们可以知道在前序遍历序列中,根节点后面的3个数字就是3个左子树节点的值,其它的是右子树的值。这样,我们就在前序遍历和中序遍历两个序列中,分别找到了左右子树对应的子序列。
接下来,我们只需要递归处理左子树和右子树就行了。
解:Java
结合前面的Java代码,实现代码如下:
public static BinaryTree construct(int preOrder[], int inOrder[]) {
if (preOrder == null || inOrder == null
|| preOrder.length != inOrder.length || preOrder.length <= 0) {
return null;
}
return constructCore(preOrder, inOrder);
}
private static BinaryTree constructCore(int[] preOrder, int[] inOrder) {
if (preOrder.length == 0 || inOrder.length == 0) {
return null;
}
int rootValue = preOrder[0];
BinaryTree root = new BinaryTree(rootValue);
if (preOrder.length == 1) {
if (inOrder[0] != rootValue) {
throw new InvalidParameterException("preOrder and inOrder not match");
}
return root;
}
// 在中序中查找根节点
int rootInorderIndex = 0;
while (rootInorderIndex < inOrder.length && inOrder[rootInorderIndex] != rootValue) {
rootInorderIndex++;
}
if (rootInorderIndex > 0) { // 构建左子树
root.left = constructCore(Arrays.copyOfRange(preOrder, 1, rootInorderIndex + 1),
Arrays.copyOf(inOrder, rootInorderIndex));
}
if (rootInorderIndex < preOrder.length) { // 构建右子树
root.right = constructCore(Arrays.copyOfRange(preOrder, rootInorderIndex + 1, preOrder.length),
Arrays.copyOfRange(inOrder, rootInorderIndex + 1, inOrder.length));
}
return root;
}
调用实例:
public static void main(String args[]) {
int[] preOrder = {1, 2, 4, 7, 3, 5, 6, 8};
int[] inOrder = {4, 7, 2, 1, 5, 3, 8, 6};
BinaryTree tree = BinaryTree.construct(preOrder, inOrder);
}
解:C++
和Java代码类似,只不过将数值引用变为了数组指针。
#include
using namespace std;
struct BinaryTreeNode {
int m_nValue;
BinaryTreeNode *m_pLeft;
BinaryTreeNode *m_pRight;
};
BinaryTreeNode *constructCore(int *startPreorder, int *endPreorder, int *stardInorder, int *endInorder) {
int rootValue = startPreorder[0]; // 前序遍历第一个值是根节点的值
BinaryTreeNode *root = new BinaryTreeNode(); // 创建根节点
root->m_nValue = rootValue;
root->m_pLeft = root->m_pRight = NULL;
if (startPreorder == endPreorder) {
if ((stardInorder == endInorder) && (*stardInorder == *startPreorder)) {
return root;
} else {
throw invalid_argument("Preorder and Inorder not match!");
}
}
// 在中序序列中找到根节点
int *rootInorder = stardInorder;
while (rootInorder <= endInorder && *rootInorder != rootValue) {
rootInorder++;
}
if (rootInorder == endInorder && *rootInorder != rootValue) {
throw invalid_argument("Preorder and Inorder not match!");
}
int leftLength = rootInorder - stardInorder;
int *leftPreorderEnd = startPreorder + leftLength;
if (leftLength > 0) { // 构建左子树
root->m_pLeft = constructCore(startPreorder + 1, leftPreorderEnd, stardInorder, rootInorder - 1);
}
if (leftLength < endPreorder - startPreorder) { // 构建右子树
root->m_pRight = constructCore(leftPreorderEnd + 1, endPreorder, rootInorder + 1, endInorder);
}
return root;
}
BinaryTreeNode *construct(int *preOrder, int *inOrder, int length) {
if (preOrder == NULL || inOrder == NULL || length <= 0) {
return NULL;
}
return constructCore(preOrder, preOrder + length - 1, inOrder, inOrder + length - 1);
}
int main() {
int length = 8;
int preOrder[] = {1, 2, 4, 7, 3, 5, 6, 8};
int inOrder[] = {4, 7, 2, 1, 5, 3, 8, 6};
BinaryTreeNode *node = construct(preOrder, inOrder, length);
return 0;
}