一维、二维数组寻找最大子数列-Kadane算法
一维数组求最大子序列
参考博客
问题: 给定一个数列,例如【−2, 1, −3, 4, −1, 2, 1, −5, 4】, 求一个连续的数列使得数列内的元素和最大, 示例中最大子数列应该是【4, −1, 2, 1】, 求和值为6。
这个问题是可以衍生到一些变种问题, 如寻找数列中最大乘积序列,且要求序列中,相邻元素间隔不超过限定值等, 常出现在笔试面试编程题中。
该问题最早于1977年提出,但是直到1984年才被Jay Kadane 发现了线性时间的最优解法,所以算法虽然长度很短,但其实并不容易理解。
算法描述:
遍历该数组, 在遍历过程中, 将遍历到的元素依次累加起来, 当累加结果小于或等于0时, 从下一个元素开始,重新开始累加。
累加过程中, 要用一个变量(max_so_far)记录所获得过的最大值,一次遍历之后, 变量 max_so_far 中存储的即为最大子片段的和值。
参考的作者用python实现,如果没学过,我用C++再描述一下。
#include C++11的标准,我的编译器竟然没有这个文件。
//#include我们也可以使用容器,就不写复杂了,具体参看https://blog.csdn.net/qq_29611345/article/details/80958664
using namespace std;
int max(int x, int y){return x > y ? x : y;}
int max_subarray(int *arr, int size){
//题目中有一个隐含的设定, 最大子片段是可以为空的, 空片段的和值是0
int max_ending_here =0;
int max_so_far = 0;
for(int i = 0; i != size; i++){
max_ending_here = max(0, max_ending_here + arr[i]);
max_so_far = max(max_so_far, max_ending_here);
}
return max_so_far;
}
int main(){
int nums[] = {1,2,3,4,-1,-2};
int numsLen = sizeof(nums) / sizeof(nums[0]);
cout<return 0;
}
//由上面改进,增加记录最大值索引下标的功能。
void MaxIntArray(int *arr, int &max_so_far, int &beginIndex, int &endIndex, int length){
int max_ending_here = 0;
max_so_far = 0;
beginIndex = -1;
endIndex = -1;
for(int i = 0; i != length; i++){
max_ending_here = max_ending_here + arr[i];
if( max_ending_here < 0){
beginIndex = i+1;
max_ending_here = 0;
}
if(max_so_far < max_ending_here){
endIndex = i;
max_so_far = max_ending_here;
}
}
}
二维数组寻找最大子数列
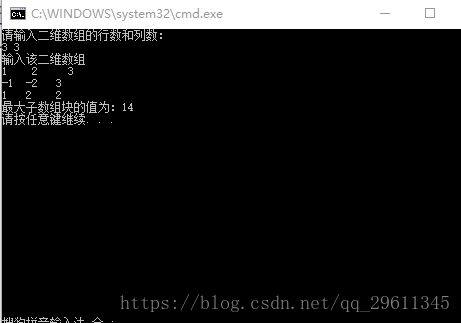
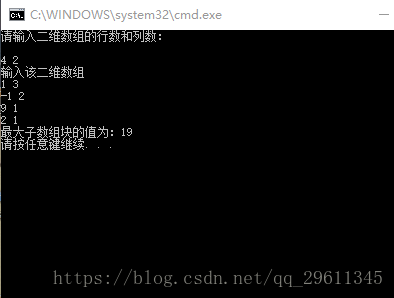
题目描述:就是一个二维数组,里面连通的的数列的最大和,不要求首尾相接,就和贪吃蛇走迷宫差不多,找到最长的贪吃蛇。
参考博客截图
参考博客说了两种方法,第一要用到栈或者队列,索引记录较为繁琐,用了第二种降维的方法。
方案二:
1.按行分组,将二维数组按行分成n个一维数组。
2.求出每个一维数组最大子数组和,并记录最大子数组和的首末位置。(一维数组的最大子数组和算法见上)
3.通过首末位置判断是否连通。如果连通则直接相加,若不连通则需要判断连通所需代价如何。
(很明显,这里需要思考的地方有两个、第一更改kadane算法是计算下标、第二、思考如何计算代价,连通上下两行,很明显这里对于第二个问题的思考鲁棒性不强,没有考虑上下不能直接连通的情形。稍后再修改这部分代码。)
#includecin>>n>>m;
int a[100][100];
int b[100];
cout<<"输入该二维数组"<for(int i=0;ifor(int j=0;jcin>>a[i][j];
//分块
int Max[100];
int Begin[100];
int End[100];
for(i=0;i//按行分组
for(int j=0;j//b是第i行的数组,第i行的最大值,第i行的起始,结束下标,数组长度。
MaxIntArray(b,Max[i],Begin[i],End[i],m);
}
int max=Max[0];
for( i=0;i1;i++)//i表示行数
{
if((Begin[i]<=End[i+1]&&Begin[i]>=Begin[i+1])||(End[i]<=End[i+1]&&End[i]>=Begin[i+1]))
{
/*
上面的意思就是,上一行到首尾两端,至少要有一端在下一行两端的内部,
这样上面的子序列可以顺利过渡到下一行,不用再添加额外的格子。
*/
max=Max[i+1]+max;
}
else
{
//如果不能直接连通,判断代价是否合适
//上一行最佳子串在下一行的后面
if(Begin[i]>End[i+1])
{
int t = Begin[i]-End[i+1];//两行间隔
int s = Begin[i]; //上一行begin下标
int temp=0;
for(int k=0;k//计算上一行begin,往下,往左到下一行end的总和。不包括end。
{
temp+=a[i+1][s-k];
}
if(temp+Max[i+1]>0)//如果小于0呢,咋办?这需要更改整个代价计算的函数,,只计算从i到i+1明显是不够的。
max=temp+Max[i+1];
}
//上一行最佳子串在下一行的前面
if(End[i]1])
{
int t = Begin[i+1]-End[i];
int s = End[i];
int temp=0;
for(int k=0;k1][s+k];
}
if(temp+Max[i+1]>0)
max=temp+Max[i+1];
}
}
}
cout<<"最大子数组块的值为:"<//计算一维最大子数组,并返回起始位置的函数
void MaxIntArray(int *arr, int &max_so_far, int &beginIndex, int &endIndex, int length){
int max_ending_here = 0;
max_so_far = 0;
beginIndex = -1;
endIndex = -1;
for(int i = 0; i != length; i++){
max_ending_here = max_ending_here + arr[i];
if( max_ending_here < 0){
beginIndex = i+1;
max_ending_here = 0;
}
if(max_so_far < max_ending_here){
endIndex = i;
max_so_far = max_ending_here;
}
}
}