残缺棋盘问题
问题描述:
三格板的覆盖形态可为以下四种
编程输出一种覆盖方案,覆盖时用上述编号表示其形态
输入: k 残缺格的坐标x,y;
输出: 数字方阵,用7表示残缺的格
解题思路:
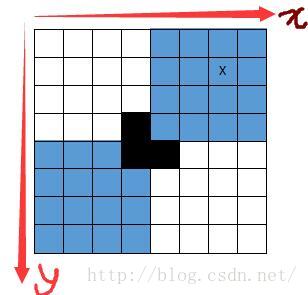
观察几组覆盖方案后得出:在2^2*2^2(k=2)的棋盘中使用三格板覆盖,必然会空出一个格
我们利用每4*4个方格阵空出的这一个格可解出k=3时,即2^3*2^3的棋盘覆盖方案,如图:
在(6,1)有一残缺的格,这时,我们三格板的第3种覆盖形态放置到(3,3)位置上,即可满足把棋盘均分为四分后对于"在2^2*2^2(k=2)的棋盘中使用三格板覆盖,必然会空出一个格"的覆盖,由此得出k=3时的解;(4*4的棋盘同样满足上述规律)
这时我们考虑解一下更大的棋盘的覆盖方案
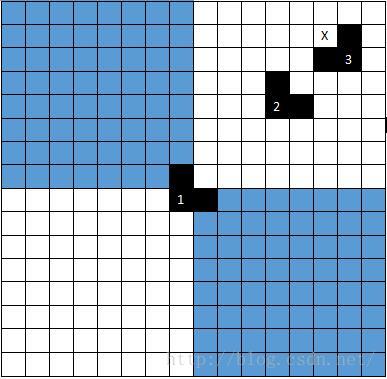
上图为k=4时的前四步解法,我们把此棋盘分割为四分就得到了四个4*4的棋盘
之前我们已经学习了这种棋盘的解法,此时我们只需把此棋盘等分四分即可得到解
等分后同样满足每份方阵都必然有一个空,此时我们使用一个1~4中任意一个三格板即可;
更大的棋盘同样满足等分四份后每份方阵进行覆盖改后都必然有一个空
上图为k=5时残缺格位置为(0,23)时的解
桑代码~
#include
#include
int in[1024][1024];
void t1(int x,int y){
in[x][y]=1;
in[x+1][y]=1;
in[x][y+1]=1;
}
void t2(int x,int y){
in[x][y]=2;
in[x+1][y]=2;
in[x+1][y+1]=2;
}
void t3(int x,int y){
in[x][y]=3;
in[x][y+1]=3;
in[x+1][y+1]=3;
}
void t4(int x,int y){//四种三格板状态
in[x+1][y]=4;
in[x+1][y+1]=4;
in[x][y+1]=4;
}
void recursion(int x1,int y1,int x2,int y2,int x3,int y3){//递归
if(x2-x1==1){//等于2*2的方阵时直接得出解
if(x3==x1){
if(y3==y1){
t4(x1,y1);
}else {
t2(x1,y1);
}
}else{
if(y3==y1){
t3(x1,y1);
}else {
t1(x1,y1);
}
}
return;
}
if(x3<=(x1+x2)/2){
if(y3>(y1+y2)/2){
t2((x1+x2)/2,(y1+y2)/2);//不可覆盖角位于:左下
recursion(x1,(y1+y2)/2+1,(x1+x2)/2,y2,x3,y3);
recursion(x1,y1,(x1+x2)/2,(y1+y2)/2,(x1+x2)/2,(y1+y2)/2);//zuoshang
recursion((x1+x2)/2+1,y1,x2,(y1+y2)/2,(x1+x2)/2+1,(y1+y2)/2);//youshang
recursion((x1+x2)/2+1,(y1+y2)/2+1,x2,y2,(x1+x2)/2+1,(y1+y2)/2+1);//youxia
}else{
t4((x1+x2)/2,(y1+y2)/2);//不可覆盖角位于:左上
recursion(x1,y1,(x1+x2)/2,(y1+y2)/2,x3,y3);
recursion((x1+x2)/2+1,y1,x2,(y1+y2)/2,(x1+x2)/2+1,(y1+y2)/2);//youshang
recursion((x1+x2)/2+1,(y1+y2)/2+1,x2,y2,(x1+x2)/2+1,(y1+y2)/2+1);//youxia
recursion(x1,(y1+y2)/2+1,(x1+x2)/2,y2,(x1+x2)/2,(y1+y2)/2+1);//zuoxia
}
}else{
if(y3>(y1+y2)/2){
t1((x1+x2)/2,(y1+y2)/2);//不可覆盖角位于:右下
recursion((x1+x2)/2+1,(y1+y2)/2+1,x2,y2,x3,y3);
recursion(x1,y1,(x1+x2)/2,(y1+y2)/2,(x1+x2)/2,(y1+y2)/2);//zuoshang
recursion(x1,(y1+y2)/2+1,(x1+x2)/2,y2,(x1+x2)/2,(y1+y2)/2+1);//zuoxia
recursion((x1+x2)/2+1,y1,x2,(y1+y2)/2,(x1+x2)/2+1,(y1+y2)/2);//youshang
}else{
t3((x1+x2)/2,(y1+y2)/2);//不可覆盖角位于:右上
recursion((x1+x2)/2+1,y1,x2,(y1+y2)/2,x3,y3);
recursion(x1,y1,(x1+x2)/2,(y1+y2)/2,(x1+x2)/2,(y1+y2)/2);//zuoshang
recursion(x1,(y1+y2)/2+1,(x1+x2)/2,y2,(x1+x2)/2,(y1+y2)/2+1);//zuoxia
recursion((x1+x2)/2+1,(y1+y2)/2+1,x2,y2,(x1+x2)/2+1,(y1+y2)/2+1);//youxia
}
}
return;
}
int main(){
int k,x,y,y2;
scanf("%d %d %d",&k,&x,&y);
printf("\n");
in[x][y]=7;
y2=pow(2,k)-1;
recursion(0,0,y2,y2,x,y);
for(int i1=0;i1