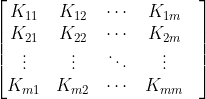【机器学习】SVM核方法

Kernel Trick

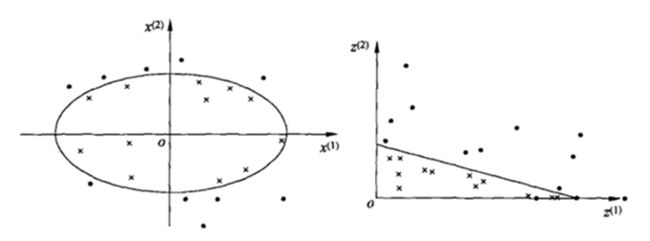
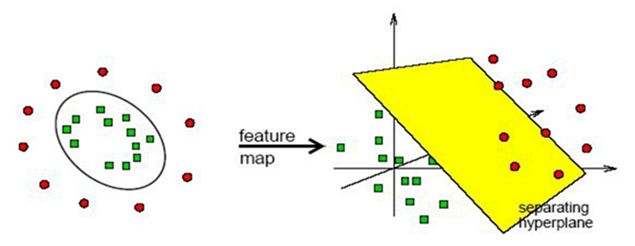
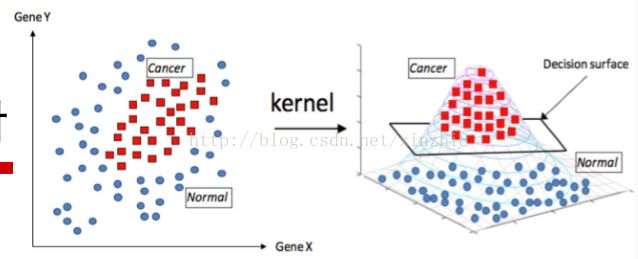
在 SVM 中引入核方法便可使得 SVM 变为非线性分类器，给定非线性可分数据集 ，如下图所示，此时找不到一个分类平面来将数据分开，核方法可以将数据投影到新空间，使得投影后的数据线性可分，下图给出一个  的映射，原空间为  ,新空间为  ，根据图可以看出映射后样本点的变化，此时样本便为线性可分的了，直接用  分类即可。

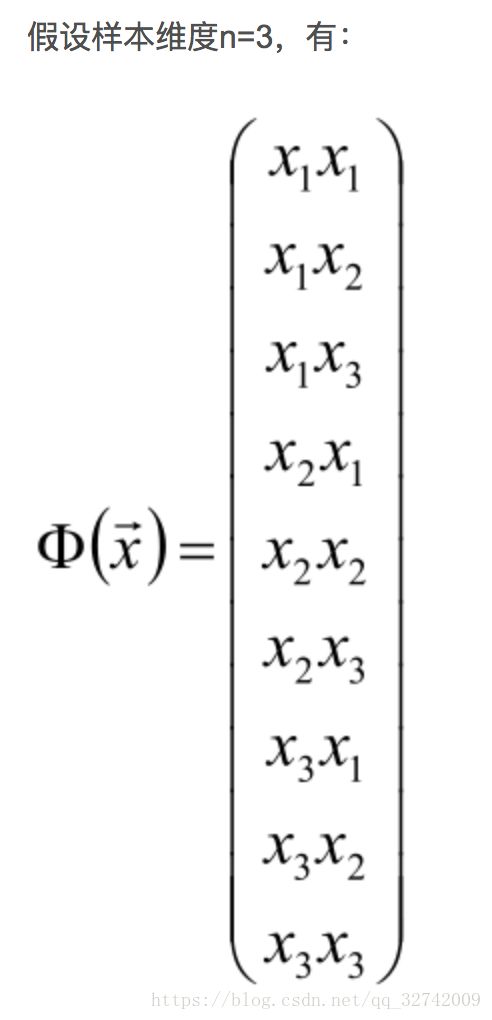
上图是一个  的映射，但一般情况下，特征空间的选取往往是很高维度的  ,如下为一个  的映射：

核函数

下面给核函数一个正式定义，设  为输入空间， 为特征空间，如果存在一个  到  的映射   ，对所有的 ，函数  满足  ,则称  为输入空间到特征空间的映射函数， 为核函数。

核函数常用的技巧是不计算映射函数  ，因为特征空间  通常是高维的，甚至无穷维，所以  计算并不容易，而计算核函数  却相对简单。映射  取法多种多样，可以取不同的特征空间，即使在同一特征空间也可以取不同的映射。映射后的样本一般是线性可分带有异常值的，这时考虑 SVM 的优化目标：

在实际优化中还需加上KKT条件。

由于在输入空间计算的是  的内积，所以经过映射后分别为  与  ，现在只需修改目标函数为   与  的内积即可，又由于   ，所以不需要定义映射函数  ，只需要定义核函数便可得到高维空间中内积的结果，而这便是 Kernel Trick。所以线性不可分的数据集的优化目标变为：

也就是说给定核函数  ，即可用求解线性 SVM 的方法来求解非线性问题，核技巧的好处在于不需要显式的定义特征空间与映射函数，只需要选择一个合适的核函数即可。综上核函数是用来免去显式计算高维变换的，直接用低维度的参数带入核函数来等价计算高维度的向量的内积。

核函数的基本作用就是接受两个低维空间里的向量，能够计算出经过某个变换后在高维空间里的向量内积值。

不用去寻找高维空间的映射函数，直接选定一个合适的核函数就好了（如高斯核就像是一个距离度量。）

---

插几句大白话，按照正常的思路来做，就是先计算出，映射到高维之后的,，然后计算与的内积，假设这个是多项式核。注意一下，这里x不是一个变量而是一个向量，那么计算需要次乘法，同理计算也需要次乘法，然后计算与的乘机又需要的乘法。

像这个例子一样。一方面乘法计算次数很多，计算代价很高。另一方面根本无法计算，例如高斯核，高斯核函数将样本映射成无穷维，无穷维的空间是无法单独计算的。

那我们如果使用核函数，以多项式核为例。

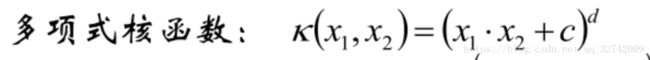
直接计算x点乘y，只需要3次乘法，然后一个平方的乘法，共4次乘法。
计算代价就降低了很多，可以传入低维的特征更高效的去计算出与不用高斯核一样的结果，不用高斯核就需要先映射到高维空间，然后两个高维特征再相乘。

核函数那么好用，当然也有自身局限。一方面在于它难以构造，另一方面在于选择一个合适的核函数也是较为困难的一件事情，需要调参不少时间。

---

核函数的选择

什么样的函数  可以作为一个有效核函数呢？答案是只要满足 Mercer 定理 即可，即如果函数  是 上的映射（ 也就是两个  维向量映射到实数域 ）。那么如果  是一个有效核函数（也称为Mercer核函数），那么当且仅当其训练样本  相应的核函数矩阵是对称半正定的，这里先解释一下正定矩阵：

对于 N 个训练样本，每一个样本  对应一个训练样例。那么，我们可以将任意两个  和  带入核函数中，计算  。这样可以把  表示为一个  的 Gram 矩阵，只要 Gram 矩阵为对称半正定的(半正定就是大于等于0)，则 即为一个有效的核函数，Gram 矩阵如下：

显然对于自己定义的核函数判定是否为正定核不太容易，所以在工业生产中一般使用一些常用的核函数，下面给出几个：

1）线性核：线性核其实就是不采用非线性分类器，认为样本是线性可分的；

2）多项式核：该核函数对应的是一个 p 次多项式的分类器，这时需要额外调节的参数为 c ，p ； 

多项式核函数可以实现将低维的输入空间映射到高纬的特征空间，但是多项式核函数的参数多，当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算。

3）高斯核(RBF核函数)：或者叫做径向基核，该核函数甚至可以将特征空间映射为无穷维，这时需要额外调节的参数为  ；

高斯径向基函数是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，该核函数是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么核函数的时候，优先使用高斯核函数。

如果  选得很大的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果  选得很小，则可以将任意的数据映射为线性可分，当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。总的来说，通过调控参数  ，高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。

越大，山顶就越尖，就越容易被线性可分，但容易过拟合。

4）sigmoid核函数：Sigmoid核函数来源于神经网络，被广泛用于深度学习和机器学习中。采用sigmoid核函数，支持向量机实现的就是一种多层神经网络。

支持向量机的理论基础决定了它最终求得的是全局最优值而不是局部最小值，也保证了它对于未知样本的良好泛化能力而不会出现过学习现象。

Algorithm 1.4

综上，给出非线性可分支持向量机的学习算法1.4：

核函数是做到了没有真正映射却达到了映射的作用。

参考文章：

SVM核函数

核函数实例