手推SVM（二）-核方法

注：核方法不仅仅在SVM中应用，它是一种思想，就像正则化一样，能应用于其他的模型。

1. 核方法思想
2. 相似性度量
3. 核方法
   3.1 kernel trick(核技巧)
   3.2 Kernel Properties(核性质)
   3.3核函数解决了非线性可分的问题
4. 常见的核函数
   4.1 线性核
   4.2 多项式核
   4.3 高斯核（RBF）
   4.4 sigmoid核
5. Kernel Logistic Regression (KLR)

1.核方法思想

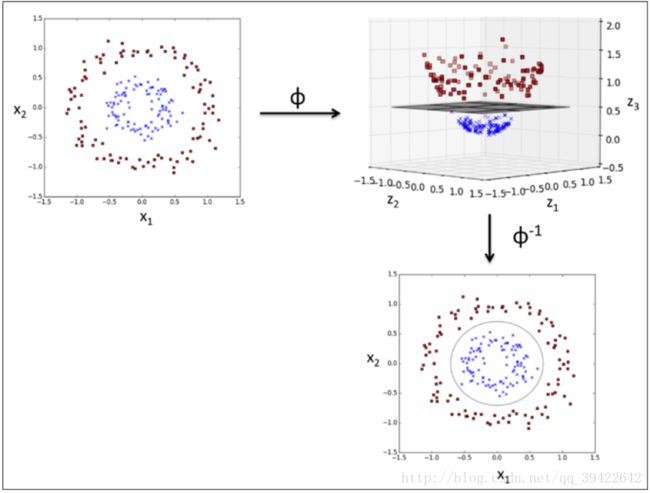
上一篇文章（手推SVM（一）-数学推导），我们看到的SVM是解决了线性问题，但对于非线性问题，比如下图中的左子图这样的数据分布，应该怎么办呢？如果SVM没有解决这个问题，它就不会长期统治那么久的机器学习界了。
上一篇文章，我们推导出:

L=∑i=1Nαi−∑j=1N∑i=1NαiαjyiyjX⃗ iX⃗ j(1)

N为样本数，如果 X⃗ i,X⃗ j 很大，很多，运算是不是就很慢了呢？那我们该怎么解决呢？
它的想法是能否找到这样一个变换 ϕ ，使得数据点经过变换后，可以在另一空间中通过某一平面分割开。

所以，按照我们的想法，我们不关心变换前 X⃗ i,X⃗ j 的点乘，我们只关心变换后：

K（X⃗ i,X⃗ j）=ϕ(X⃗ i)⋅ϕ(X⃗ j)

的点乘，其中变换后两个点的点乘就是所谓的核函数。

对（1）， α 的参数可以表示为： qi,j=yiyjK(X⃗ i,X⃗ j) 回想上一篇文章，用同样的方法可以求出最优的 α , w 很容易求，但 b 怎么办呢？我们看一下上次求b用的是什么方法：

b=yi−(w⃗ X⃗ i)

我们的 w⃗ =∑j=1NαjyjX⃗ j ,我们把 w⃗  代进去，惊奇的发现：

b=yi−(∑i,j=1NαiyiX⃗ j)X⃗ j=yi−∑i,j=1NαiyiK(X⃗ i,X⃗ j)

如此，也可以用核函数，进行转换后再求b.

对于判断一个测试样本为正/负样本的假设：

gsvm(x)=sign(w⃗ ∗ϕ(x)+b)=sign(∑i=1NαiyiK(xi,x)+b)

最后发现，所有参数，都可以通过用核函数变换后求解，而最后预测的时候，就可以只用支持向量来预测就OK了，这就大大减少了计算量。

2.相似性度量

那比较常见的就是kernel函数就是：

RBF:K(xi,xj)=similarity(xi,xj)=exp(−||xi−xj||22σ2)

多项式核：K(xi,xj)=similarity(xi,xj)=(xi⋅xj+1)n

相当于衡量两个样本的相似性。

两个样本 xi,xi 有两种情况：

两点非常接近：K(xi,xj)=exp(0)=1

两点离得非常远：K(xi,xj)=exp(−∞)=0

其中 σ 是核函数中的参数，我们用一个例子解释一下：

• 假设现在我们的训练实例样本 xi,xj 中只有两个特征,不同的 σ 值有下图：

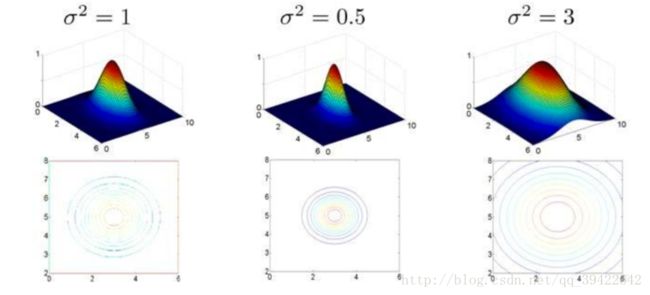
其中水平面坐标分别为两个特征，而垂直坐标轴代表了K，可以看出当两个样本 xi,xj 重合时，K才具有最大值，K值改变的速率受 σ2 的影响。

从这个角度来看，可以把核函数在其中发挥的作用当成是衡量两个样本的相似性的度量。

其实这并不稀奇，kernel不仅可以建立点对点的映射，而且可以建立某一分布到点的映射，在这样的映射下，人们会更关心这样一个问题：

• 给定两组数据，如何知道他们是不是属于同一个分布的？

简单直接的办法就是把他们映射到同一个kernel space中，然后看他们对应的点是不是很接近或者重合，如果是，这两组数据就应该是属于同一个分布的，这也是相似性度量的一种。

3.核方法

核方法是一种用于模式识别和分析的算法，最开始是由SVM导出的，模式分析的主要任务就是从数据中，比如文本数据，图像数据，找出相关性，但核方法不仅仅用于SVM，它更多的是一种思想，还被用于其他从线性问题转为非线性问题的问题中，比如ridge regression等算法。

核方法的主要特点就是它对问题的不同处理方法。它的核心思想是将数据映射到高维空间中，希望在高维空间中数据具有更好的区分性，而核函数是用来计算映射到高维空间中内积的一种方法，也就是说核方法的本质应该是内积，而内积又恰恰定义了相似度。

3.1 kernel trick(核技巧)

kernel trick,不知道翻译为核技巧是否合理，总之，它是一种非常强大的工具，因为它通过点乘，给线性问题和非线性问题提供了连接的桥梁。如果我们把输入数据先映射到高维空间，线性算法在这个空间中计算，对于原始空间来说，就会变成非线性算法。

可视化图像：youtube上的核函数作用原理

那具体巧在哪里呢？如果我们想对线性不可分的数据进行分类，
从两方面入手：

1. soft margin:即容忍模型有一定的容错能力
2. Input Space做Feature Expansion，把数据集映射到高维中去，形成了Feature Space。我们可以认为在原本空间中线性不可分的数据在映射之后的空间中一定存在一个超平面把它们区分开。然后再用优化方法优化，找出这样的超平面。

trick 的具体意义是：简化在二次规划的中间一步的内积计算。即中间有一步是求 ϕ(xi)′ϕ(xj) 的，而我们可以定义核函数 K(xi,xj)=ϕ(xi)′ϕ(xj) ,使得我们不需要计算每个 ϕ(xi)′,ϕ(xj) ,就可以直接求出 ϕ(xi)′ϕ(xj) 了。

核技巧是非常有趣的，因为它甚至不需要计算。如果一个算法可以用内积表示，我们就可以用合适的其他空间中的内积来代替这个内积的运算，所谓“技巧“，就是这个内积可以用核函数代替，核函数可以表示为特征空间中的内积，通常被表示为：

K(x,y)=<ϕ(x),ϕ(y)>

3.2 Kernel Properties(核性质)

同时，一般需要满足这样两个条件：

第一个条件要求核函数的结果满足一定的概率密度函数；第二个要求对应分布的平均值与原来的分布一样。

核函数必须是连续的，对称的，而且应该有一个正定（半正定）的Gram 矩阵，它的所有特征值都是非负的，从而确保了其对应的优化问题是凸的，且解是唯一的。

核函数还不止我上面提到的那几个，同时核函数的选择也是高度依赖我们手中的问题核数据集的，也高度依赖于模型，所以选择的时候尽量先用线性的，不行再用其他复杂的，比如RBF核。

3.3核函数解决了非线性可分的问题

如图所示，核函数主要解决的是数据的非线性可分问题，那它是怎么实现的呢？
为了让大家理解，我举个简单的例子，假设有一个非线性可分的问题，是在二维平面上，如果用 X1 和 X2 来表示这个二维平面的两个坐标的话，我们知道一条二次曲线（圆圈是二次曲线的一种特殊情况）的方程可以写作这样的形式：

a1X1+a2X21+a3X2+a4X22+a5X1X2+a6=0

注意上面的形式，如果我们构造另外一个五维的空间，其中五个坐标的值分别为 Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2，那么显然，上面的方程在新的坐标系下可以写作：

∑iaiZi+a6=0

发现这其实就是一个线性的函数，也就是说，通过这样的简单的映射，可以使在原来空间中非线性可分的问题，转换为在新空间中的线性可分为问题。

4.常见的核函数

4.1 线性核
线性核是最简单的核函数，只要做一个内积就差不多了，

主要用于线性可分的情形。参数少，速度快，对于一般数据，分类效果已经很理想了。

4.2 多项式核
多项式核适合所有的训练数据都是标准化之后的

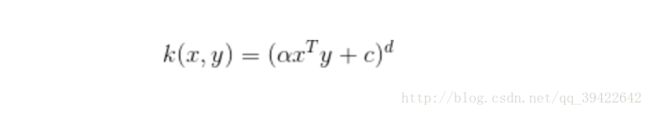
4.3 高斯核（RBF）

也可写为：

它是radial basis function的核， γ 在其中扮演着非常重要的角色，如图所示：如果取得不合适，就非常容易造成过拟合。

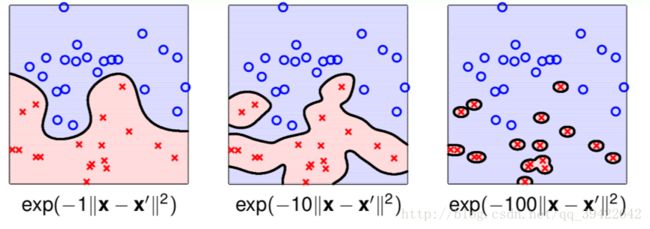
主要用于线性不可分的情形。参数多，分类结果非常依赖于参数。有很多人是通过训练数据的交叉验证来寻找合适的参数，不过这个过程比较耗时。但一旦能找到好的参数，效果就非常好。
它的推导过程如下：

4.4 sigmoid核

在选用核函数的时候，我们必须对数据有一个先验的理解，然后根据我们的理解选择核函数，又或者通过交叉验证的方式寻找使得误差最小的核函数，常用的核函数选择方法如下：

• 如果样本的数量和特征的数量基本一致，选择线性核的SVM
• 如果特征的数量特别少，而样本的数量正常，可以选用高斯核RBF
• 如果特征数量少，但样本的数量很大，可以手动添加特征，选用更多的特征组合方式，或者选用分类能力强的特征进行特征组合

5.Kernel Logistic Regression (KLR)

KL模型相当于是逻辑回归和核方法的结合使用，其基本的思想是先对数据进行SVM训练预测，得到分数再通过对应的逻辑回归映射：

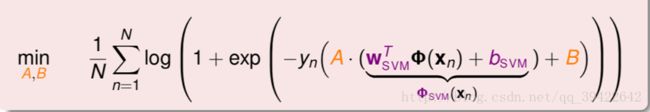
可以从两方面理解这个公式：

wTsvmϕ(xn)+bsvm

相当于一个SVM，用来映射训练数据，相当于用了kernel trick,固定住了超平面，而A的作用是对SVM得到的结果进行放缩，而B的作用则是平移。在外面再套一个logREG,去微调超平面，相当于逻辑回归中的最大似然估计。

所以这个过程可以分为两个阶段的学习：

1. 做SVM，结果作为转换，将数据转换到一维空间中
2. 在一维空间中做简单的线性回归问题

最后经过化简，还可以表示成：

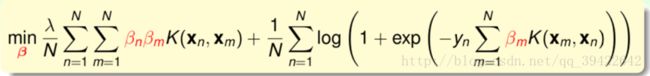
即核函数表示，这其实是一个关于 β 的无条件优化问题。

参考
支持向量机（四）– 核函数
svm常用核函数
机器学习技法
SVM的核函数如何选取？
Kernel Functions for Machine Learning Applications
What are kernels in machine learning and SVM and why do we need them?

第一版
2017.12.8

第二版
2017.12.11
增加KLR的简单理解