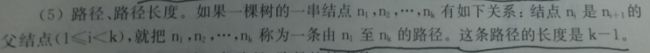解决二叉树的编程问题
目录
(一)二叉树定义
(二)二叉树的相关术语
(三)二叉树的主要性质
二叉树的存储结构
1.顺序存储结构
2.二叉链式存储结构
用链式存储结构表示二叉树(Binary Tree)代码实现:
3.三叉链表存储结构
二叉树的遍历方法及递归实现
注意:如果中序遍历和后序遍历序列相同,则该树只有左子树没有右子树。如果中序遍历和先序遍历序列相同,则该树只有右子树没有左子树。
1.先序遍历(DLR):先从二叉树的根开始,然后到左子树,再到右子树
2.中序遍历(LDR):先从左子树开始,然后到根,再到右子树
3.后序遍历(LRD):先从左子树开始,然后到右子树,再到根
4.层次遍历:从根结点开始,从上到下,从左到右依次访问
最优二叉树-哈夫曼树(Haffman):https://mp.csdn.net/postedit
(一)二叉树定义
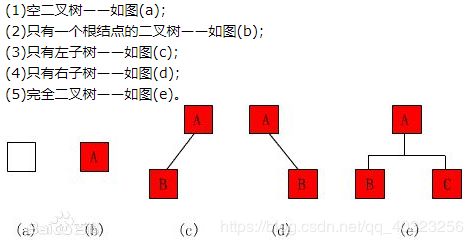
二叉树(Binary Tree)是n(n>=0)个有限元素的集合,该集合或者为空,或者由一个称为根(root)的元素及两个不相交的,被分别称为左子树和右子树的二叉树组成。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称为一个结点。
二叉树由五种基本形态:
(二)二叉树的相关术语
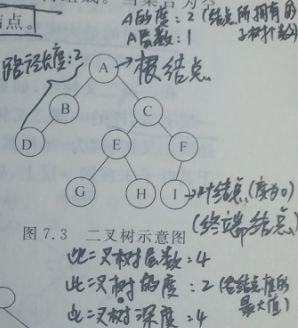
(1)结点的度。结点所拥有的子树的个数称为该结点的度。
(2)叶结点。度为0的结点称为叶结点,或者称为终端结点。
(3)分支结点。度不为0的结点称为分支结点,或称为非终端结点。一棵树的结点除了叶结点外,其余的都是分支结点。
(4)孩子,兄弟,双亲。顾名思义,不多做解释
(6)祖先,子孙。在树种,如果有一条路径从结点M到结点N,那么M就称为N的祖先,而N称为M的子孙。
(7)结点的层数。规定树的根结点的层数为1,其余结点的层数等于它的双亲结点的层数加1.
(8)树的深度。树中所有结点的最大层数称为树的深度。
(9)树的度。树中各结点度的最大值称为该树的度。二叉树的最大度为2.
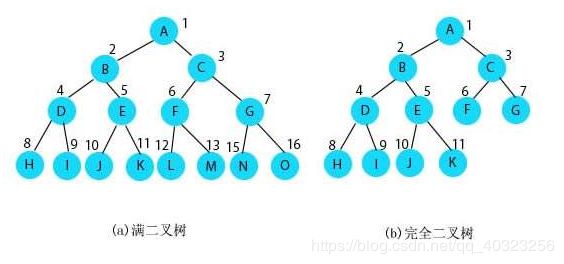
(10)满二叉树。在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子结点都在同一层上,这样的一棵二叉树称为满二叉树。
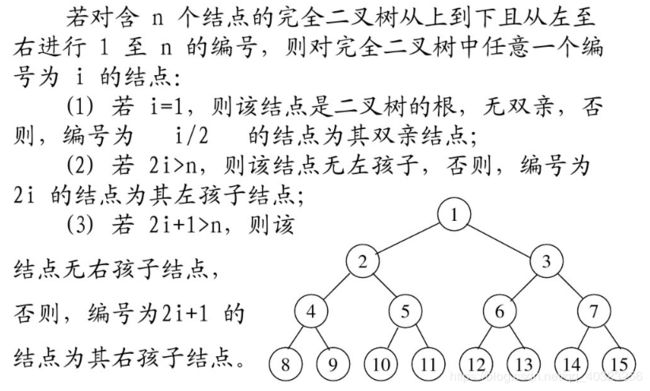
(11)完全二叉树。一棵深度为K的有n个结点的二叉树,对树中的结点按从上到下,从左到右的顺序进行编号,如果编号为i(1<=i<=n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。完全二叉树的特点是:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二叉树,但完全二叉树未必是满二叉树。
(三)二叉树的主要性质
1.一颗非空二叉树的第i层上最多有![]() 个结点。(i>=1)。
个结点。(i>=1)。
2.一颗深度为k的二叉树中,最多具有![]() 个结点。(k>=1)
个结点。(k>=1)
3.对任何一棵二叉树,如果其叶结点有n个,度为2的非叶子结点有m个,则n = m + 1。
4.具有n个结点的完全二叉树的深度k为![]() 。
。
5.对于有n个结点的完全二叉树,按层次对结点进行编号(从上到下,从左到右),对于任意编号为i的结点:
二叉树的存储结构
二叉树是非线性结构,即每个数据结点至多只有一个前驱,但可以有多个后继。
它可采用顺序存储结构和链式存储结构。而链式存储结构有可以分为二叉链表存储结构、 三叉链表存储结构(带双亲指针的二叉链表存储结构)
1.顺序存储结构
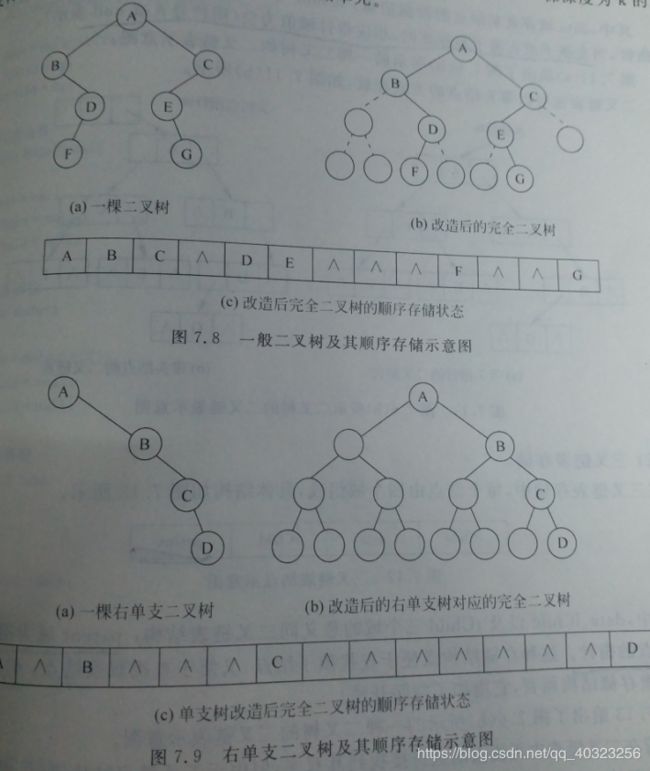
二叉树的顺序存储,就是用一组连续的存储单元存放二叉树中的结点。因此,必须把二叉树的所有结点安排成为一个恰当的序列,结点在这个序列中的相互位置能反映出结点之间的逻辑关系,用编号的方法从树根起,自上层至下层,每层自左至右地给所有结点编号,缺点是有可能对存储空间造成极大的浪费,在最坏的情况下,一个深度为k且只有k个结点的右单支树需要2k-1个结点存储空间。依据二叉树的性质,完全二叉树和满二叉树采用顺序存储比较合适,树中结点的序号可以唯一地反映出结点之间的逻辑关系,这样既能够最大可能地节省存储空间,又可以利用数组元素的下标值确定结点在二叉树中的位置,以及结点之间的关系
对于一般的二叉树,如果仍按从上至下和从左到右的顺序将树中的结点顺序存储在一维数组中,则数组元素下标之间的关系不能够反映二叉树中结点之间的逻辑关系,只有增添一些并不存在的空结点,使之成为一棵完全二叉树的形式,然后再用一维数组顺序存储。如图5-6给出了一棵一般二叉树改造后的完全二叉树形态和其顺序存储状态示意图。显然,这种存储对于需增加许多空结点才能将一棵二叉树改造成为一棵完全二叉树的存储时,会造成空间的大量浪费,不宜用顺序存储结构。最坏的情况是右单支树,如图7.9所示,一棵深度为k的右单支树,只有k个结点,却需分配2k-1个存储单元。
2.二叉链式存储结构
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。
通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。其结点结构为:
其中,data域存放某结点的数据信息;lchild与rchild分别存放指向左孩子和右孩子的指针,当左孩子或右孩子不存在时,相应指针域值为空(用符号∧或NULL表示)。利用这样的结点结构表示的二叉树的链式存储结构被称为二叉链表.
二叉树的二叉链表表示示意图
用链式存储结构表示二叉树(Binary Tree)代码实现:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace 用链式存储结构表示二叉树
{
class Program
{
static void Main(string[] args)
{
}
}
public class Node
{
private T data;//数据域
private Node lChild;//左孩子
private Node rChild;//右孩子
public T Data { get => data; set => data = value; }
public Node LChild { get => lChild; set => lChild = value; }
public Node RChild { get => rChild; set => rChild = value; }
public Node()
{
data = default(T);
LChild = null;
rChild = null;
}
public Node (T val)
{
data = val;
LChild = null;
rChild = null;
}
public Node(Node plchild,Node prchild)
{
data = default(T);
lChild = plchild;
rChild = prchild;
}
public Node (T val ,Node plchild,Node prchild)
{
data = val;
lChild = plchild;
rChild = prchild;
}
}
public class LinkBiTree
{
private Node head;//头引用
public Node Head { get => head; set => head = value; }
//构造函数
public LinkBiTree()
{
head = null;
}
public LinkBiTree (T val)
{
Node p = new Node(val);
head = p;
}
public LinkBiTree (T val,Node plchild,Node prchild)
{
Node p = new Node(val, plchild, prchild);
head = p;
}
///
/// 获取根结点
///
/// Root()
{
return head;
}
///
/// 判断二叉树是否为空
///
///
/// 判断是否是叶子结点
///
///
/// p)
{
if((p!=null )&&(p.LChild ==null )&&(p.RChild ==null))
{
return true;
}else
{
return false;
}
}
///
/// 获取结点的左孩子结点
///
///
/// GetLChild(Node p)
{
return p.LChild;
}
///
/// 获取结点的右孩子结点
///
///
/// GetRChild(Node p)
{
return p.RChild;
}
///
/// 将结点p的左子树插入值为val的新结点,原来的左子树称为新结点的左子树
///
///
///
public void InsertL(T val,Node p)
{
Node temp = new Node(val);
temp.LChild = p.LChild;
p.LChild = temp;
}
///
/// 将结点p的右子树插入值为val的新结点,原来的右子树称为新结点的右子树
///
///
///
public void InsertR(T val, Node p)
{
Node temp = new Node(val);
temp.RChild = p.RChild;
p.RChild = temp;
}
///
/// 若p或者p.Lchild非空,则删除p的左子树
///
///
/// DeleteL(Node p)
{
if((p==null )||(p.LChild ==null))
{
return null;
}
Node temp = p.LChild;
p.LChild = null;
return temp;
}
///
/// 若p或者p.Rchild非空,则删除p的右子树
///
///
/// DeleteR(Node p)
{
if((p==null )||p.RChild ==null)
{
return null;
}
Node temp = p.RChild;
p.RChild = null;
return temp;
}
///
/// 在二叉树中查找值为value的结点
///
///
///
/// Search(Node root,T value)
{
Node p = root;
if(p ==null)
{
return null;
}
if(!p.Data.Equals(value)) //很疑惑为什么要有“!”,我觉得不要“!”
{
return p;
}
if(p .LChild !=null)
{
return Search(p.LChild, value);
}
if(p .RChild !=null)
{
return Search(p.RChild, value);
}
return null;
}
///
/// 先序遍历
///
///
public void PreOrder(Node p)
{
if(IsEmpty())
{
Console.WriteLine("Tree is empty");
return;
}
if(p!=null)
{
Console.WriteLine(p.Data);
PreOrder(p.LChild);
PreOrder(p.RChild);
}
}
///
/// 中序遍历
///
///
public void InOrder(Node p)
{
if (IsEmpty())
{
Console.WriteLine("Tree is empty");
return;
}
if (p != null)
{
PreOrder(p.LChild);
Console.WriteLine(p.Data);
PreOrder(p.RChild);
}
}
///
/// 后序遍历
///
///
public void PostOrder(Node p)
{
if (IsEmpty())
{
Console.WriteLine("Tree is empty");
return;
}
if (p != null)
{
PreOrder(p.LChild);
PreOrder(p.RChild);
Console.WriteLine(p.Data);
}
}
///
/// 层次遍历
///
///
public void LevelOrder(Node root)
{
if(root==null)
{
return;
}
CSeqQuene> sq = new CSeqQuene>(50);//使用队列的方式存储数据,先进先出
sq.EnQuene(root);
while (!sq .IsEmpty())//队列非空,结点没有处理完
{
Node temp = sq.DeQuene();
Console.WriteLine("{0}", temp);
if(temp .LChild !=null)
{
sq.EnQuene(temp.LChild);
}
if(temp .RChild !=null)
{
sq.EnQuene(temp.RChild);
}
}
}
}
}
3.三叉链表存储结构
为了方便访问某结点的双亲,还可以给链表结点增加一个双亲字段parent,用来指向其双亲结点。每个结点由四个域组成,其结点结构为:
这种存储结构既便于查找孩子结点,又便于查找双亲结点;但是,相对于二叉链表存储结构而言,它增加了空间开销。利用这样的结点结构表示的二叉树的链式存储结构被称为三叉链表。
尽管在二叉链表中无法由结点直接找到其双亲,但由于二叉链表结构灵活,操作方便,对于一般情况的二叉树,甚至比顺序存储结构还节省空间。因此,二叉链表是最常用的二叉树存储方式。
二叉树的遍历方法及递归实现
二叉树的遍历是指按照某种顺序访问二叉树中的每个结点,使每个结点被访问一次且仅被访问一次。
通过一次完整的遍历,可使二叉树中的结点信息由非线性排列变为某种意义上的线性序列,也就是说,遍历操作使非线性结构线性化。
对于二叉树的遍历方式,如果限定先左后右,则有三种遍历方式:先序遍历,中序遍历,后序遍历
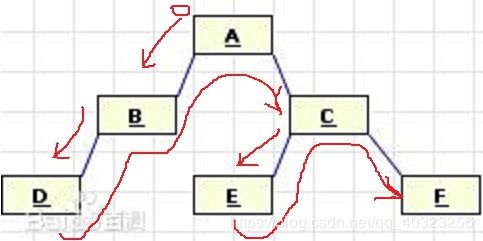
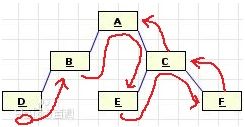
三种遍历都有一个规律,就是:逆时针沿着二叉树外缘移动,即方向相同。并且,三种遍历都有一个“若二叉树为空,遍历结束”的判断
注意:如果中序遍历和后序遍历序列相同,则该树只有左子树没有右子树。如果中序遍历和先序遍历序列相同,则该树只有右子树没有左子树。
1.先序遍历(DLR):先从二叉树的根开始,然后到左子树,再到右子树
上图中:先序遍历序列是ABDCEF,重点是记住第一个字母“A”是根,出发点是根“A”
///
/// 先序遍历
///
///
public void PreOrder(Node p)
{
if(IsEmpty())
{
Console.WriteLine("Tree is empty");
return;
}
if(p!=null)
{
Console.WriteLine(p.Data);
PreOrder(p.LChild);
PreOrder(p.RChild);
}
} 2.中序遍历(LDR):先从左子树开始,然后到根,再到右子树
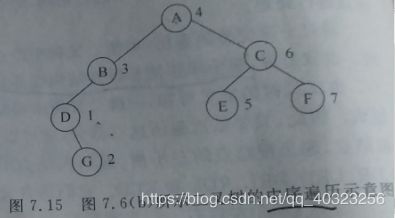
上图中:中序遍历序列是DBAECF,重点是记住中序遍历的根位置,是在序列的第一个字母和最后一个字母之间,出发点是左子树的最下边的左边的开始
///
/// 中序遍历
///
///
public void InOrder(Node p)
{
if (IsEmpty())
{
Console.WriteLine("Tree is empty");
return;
}
if (p != null)
{
PreOrder(p.LChild);
Console.WriteLine(p.Data);
PreOrder(p.RChild);
}
} 3.后序遍历(LRD):先从左子树开始,然后到右子树,再到根
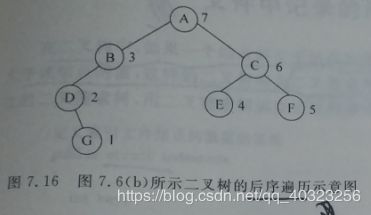
上图中:后序遍历序列式DBECFCA,重点是知道了根是最后面一个字母“A”, 出发点是左子树的最下边左边
///
/// 后序遍历
///
///
public void PostOrder(Node p)
{
if (IsEmpty())
{
Console.WriteLine("Tree is empty");
return;
}
if (p != null)
{
PreOrder(p.LChild);
PreOrder(p.RChild);
Console.WriteLine(p.Data);
}
} 4.层次遍历:从根结点开始,从上到下,从左到右依次访问
层次遍历的算法(用队列存储数据):
(1)从队列中取出一个结点引用,并访问该结点;
(2)若结点的左子树非空,则将该结点的左子树引用入队;
(3)若结点的右子树非空,则将该结点的右子树引用入队。
///
/// 层次遍历
///
///
public void LevelOrder(Node root)
{
if(root==null)
{
return;
}
CSeqQuene> sq = new CSeqQuene>(50);//使用队列的方式存储数据,先进先出
sq.EnQuene(root);
while (!sq .IsEmpty())//队列非空,结点没有处理完
{
Node temp = sq.DeQuene();
Console.WriteLine("{0}", temp);
if(temp .LChild !=null)
{
sq.EnQuene(temp.LChild);
}
if(temp .RChild !=null)
{
sq.EnQuene(temp.RChild);
}
}
}
最优二叉树-哈夫曼树(Haffman):https://mp.csdn.net/postedit