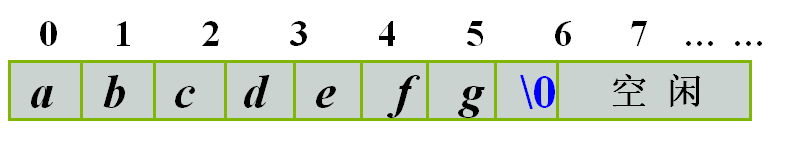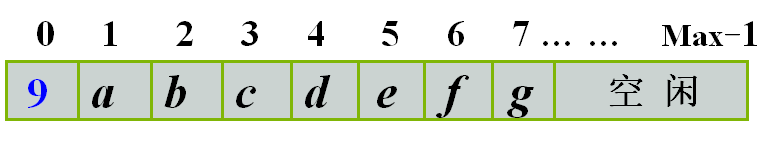数据结构——字符串和数组知识总结
一、字符串
1、字符串术语
字符串(串):零个或多个字符组成的有限序列
串长度:串中所包含的字符个数
空串:长度为0的串,记为:" "
非空串:S=" s1 s2 …… sn "(S是串名,双引号是定界符,双引号引起来的部分是串值 ,si(1≤i≤n)是一个任意字符。)
子串:串中任意个连续的字符组成的子序列。
主串:包含子串的串。
子串的位置:子串的第一个字符在主串中的序号。
2、字符串的存储结构
字符串是数据元素为单个字符的线性表,一般采用顺序结构存储,即用数组存储串的字符序列。
一般有三种方法:
方案1:用一个变量来表示串的实际长度。
方案2:在串尾存储一个不会在串中出现的特殊字符作为串的终结符,表示串的结尾。
方案3:用数组的0号单元存放串的长度,从1号单元开始存放串值。
3、模式匹配:
给定主串S="s1s2…sn"和模式T="t1t2…tm",在S中寻找T 的过程称为模式匹配,T称为模式。
4、BF算法:
从主串S的第0个字符开始和模式T 的第0个字符进行比较, 若相等,则继续比较两者的后续字符; 否则,从主串S的第1个字符开始和模式T 的第0个字符进行比较,重复上述过程,直到T 中的字符全部比较完毕,则说明本趟匹配成功;或S中字符全部比较完,则说明匹配失败。
1. 在串S和串T中设比较的起始下标i和j;
2. 循环直到S或T的所有字符均比较完;
2.1 如果S[i]==T[j],继续比较S和T的下一个字符;
2.2 否则,将i和j回溯(i=i-j+1,j=0),准备下一趟比较;
3. 如果T中所有字符均比较完,则匹配成功,返回匹配的起始比较下标(i-j);否则,匹配失败,返回-1
int BF(char S[ ], char T[ ])
{
i=0; j=0;
while (i
{
if (S[i]==T[j]) {
i++; j++;
}
else {
i=i-j+1; j=0;
}
}
if (j>=T.length()) return (i-j);
else return -1;
}
设串S长度为n,串T长度为m,时间复杂度为:
Pi 表示在第i个位置上匹配成功的概率,Pi=1/(n-m+1)。
5、KMP算法 :
主串不回溯,模式就需要向右滑动一段距离。(i不移动,j>=0的位置继续进行下一次的比较),
k=next[j-1](由next[]的 定义可以知道:t0t1…tk-1= tj-k…tj-3tj-2)
如果t[k]==t[j-1]或k==-1(不存在长度相同的前缀子串和左子串 )则t0t1…tk-1tk= tj-k…tj-3tj-2tj-1,因此 next[j]=k+1,next[j]计算结束。否则, 查找t0t1…tk的最长左子串, k=next[k],转 1 继续执行。
int KMP_FindPat(char *s, char *t,int *next){
int i=0,j=0,k;
while(s[i]!='\0' && t[j]!='\0') {
if(j==-1 || s[i]==t[j]) {
i++;
j++;
}
else
j=next[j];
}
if(t[j]=='\0')
return i-j;
else
return -1;
}
二、数组
1、数组的定义
数组是由一组类型相同的数据元素构成的有序集合,每个元素受n(n≥1)个线性关系的约束,并称该数组为 n 维数组。
2、数组的特点
二维数组是数据元素为线性表的线性表。
3、数组的基本操作
⑴ 存取:给定一组下标,读出对应的数组元素;
⑵ 修改:给定一组下标,存储或修改与其相对应的数组元素。
存取和修改操作本质上只对应一种操作——寻址
数组没有插入和删除操作,所以采用顺序存储。
常用的映射方法有两种:
按行优先:先行后列,先存储行号较小的元素,行号相同者先存储列号较小的元素。
按列优先:先列后行,先存储列号较小的元素,列号相同者先存储行号较小的元素。
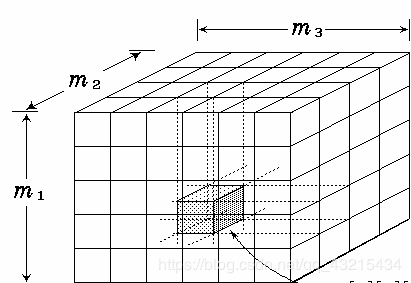
4、三维数组
说明:各维的下标从0开始
三、矩阵:
1、矩阵
特殊矩阵和稀疏矩阵
特殊矩阵:矩阵中很多值相同的元素并且它们的分布有一定的规律。
稀疏矩阵:矩阵中有很多零元素。
2、矩阵的压缩存储
压缩存储的基本思想是:
⑴ 为多个值相同的元素只分配一个存储空间;
⑵ 对零元素不分配存储空间。
3、特殊矩阵的压缩存储:
对称矩阵 :只存储下三角部分的元素。
三角矩阵 :只存储上三角(或下三角)部分的元素。
下三角矩阵:
上三角矩阵:
对角矩阵 (带状矩阵):所有非零元素都集中在以主对角线为中心的带状区域中,除了主对角线和它的上下方若干条对角线的元素外,所有其他元素都为零。 二维数组法。
4、稀疏矩阵的压缩存储
①三元组顺序表
将稀疏矩阵中的每个非零元素表示为:
(行号,列号,非零元素值)——三元组
template
struct element
{
int row, col; //行号,列号
T item //非零元素值
};
三元组表:将稀疏矩阵的非零元素对应的三元组所构成的集合,按行优先的顺序排列成一个线性表。
存储结构定义:
const int MaxTerm=100;
template
struct SparseMatrix
{
T data[MaxTerm]; //存储非零元素
int mu, nu, tu; //行数,列数,非零元个数
};
②十字链表
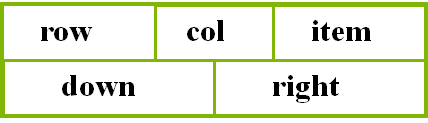
采用链接存储结构存储三元组表,每个非零元素对应的三元组存储为一个链表结点,结构为:
row:存储非零元素的行号
col:存储非零元素的列号
item:存储非零元素的值
right:指针域,指向同一行中的下一个三元组
down:指针域,指向同一列中的下一个三元组
十字链表结点类的定义:
template
class OLNode
{
public:
int row,col;
T element;
OLNode
public:
OLNode(){right=NULL;down=NULL;};
};
四、广义表
LS = (a0, a1, a2, …, an-1)
LS是表名,ai是表元素,它可以是表 (称为子表),可以是数据元素(称为原子)。
n为表的长度。n = 0 的广义表为空表。
长度:广义表LS中的直接元素的个数;
深度:广义表LS中括号的最大嵌套层数。
表头:广义表LS非空时,称第一个元素为LS的表头;
表尾:广义表LS中除表头外其余元素组成的广义表。
2、广义表与线性表的区别:
4、广义表的存储结构——头尾表示法
tag:区分表结点和元素结点的标志;
hp:指向表头结点的指针;
tp:指向表尾结点的指针;
data:数据域,存放单元素。
定义结点结构
enum Elemtag {Atom, List};
template
struct GLNode {
Elemtag tag;
union {
T data;
struct
{
GLNode *hp, *tp;
} ptr;
};
};5、广义表的特点