DFS(深搜)和BFS(广搜)

DFS(深搜)和BFS(广搜)

DFS

深度优先搜索属于图算法的一种，英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次.

举例说明：

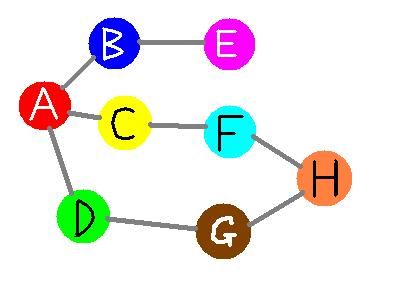
上图是无向图，从A节点开始进行深度优先搜索（以下的访问次序并不是唯一的，第二个点既可以是B也可以是C,D），则我们可能得到如下的一个访问过程：

A->B->E（没有路了！回溯到B，发现还是没路，回溯到A)->C->F->H->G->D（没有路，最终回溯到A，发现A也没路了）本次搜索结束。

注意：每次到最后一个没有路的节点时，标记已经走过，上图例子中第一个没有路的节点时E，然后回溯到B，发现B也没有路了，标记走过，再回溯到A，以此类推。

举例

题目描述
​ 在一个 w∗h的矩形广场上，每一块 1∗1的地面都铺设了红色或黑色的瓷砖。小明现在站在某一块黑色的瓷砖上，他可以从此处出发，移动到上下左右四个相邻的且是黑色的瓷砖上。现在，他想知道，通过重复上述移动所能经过的黑色瓷砖数。

输入
​ 第一行两个正整数 h,w。（2≤h,w≤50）
​ 接下来输入一个二维字符矩阵，每个字符为 “.”,"#","@"，分别代表黑色瓷砖，红色瓷砖，初始位置。

输出
​ 输出一个整数，表示可以到达的瓷砖数。

 样例输入
11 9
.#.........
.#.#######.
.#.#.....#.
.#.#.###.#.
.#.#..@#.#.
.#.#####.#.
.#.......#.
.#########.
.........

样例输出
59

数据规模与约定
​ 时间限制：1 s
​ 内存限制：256 M
100% 的数据保证 2≤h,w≤50​

​ 思路：从一个起点找到可走路径，标记已走过，递归调用
注意：需将此处的行列与坐标纸上的x,y区分开

#include 
using namespace std;

int h,w,tx,ty;
char mmap[55][55] = {0};
int ans = 1;
int dir[4][2] = {
    0,1,
    1,0,
    0,-1,
    -1,0
};


void func(int tx,int ty){
    if(tx < 0 ||tx >= w || ty < 0 || ty >= h){ //越界条件
        return ;
    }
    for(int i = 0; i < 4; i++){ //四个方向
        int x = tx + dir[i][0];
        int y = ty + dir[i][1];
        if(mmap[x][y] == '.'){
            mmap[x][y] = 0;
            ans++;
            func(x,y);
        }
    }

}


int main(){
    cin >> h >>w;
    for(int i = 0; i < w; i++){
        for(int j = 0; j < h; j++){
            cin >> mmap[i][j];
            if(mmap[i][j] == '@'){
                tx = i;
                ty = j;
            }
        }
    }
    func(tx,ty);
    cout << ans << endl;
    return 0;
}

上述题目的解法一般用在求图中黑色的数量，波数等问题。

题目描述
​ 给出 n 件物品，每个物品有一个体积 Vi，从中取出若干件物品能够组成的不同的体积和有多少种可能。例如，n=3 , Vi={1,3,4}，那么输出 6 种不同的体积和为 1,3,4,5,7,8。

输入
​ 第一行一个正整数 n。（n≤20）
​ 第二行 n 个整数，表示 Vi。（1≤Vi≤50）

输出
​ 输出一个整数，表示不同体积的组合数。

样例输入
3
1 3 4

样例输出
6

数据规模与约定
​ 时间限制：1 s
​ 内存限制：256 M
​ 100% 的数据保证 n≤20

#include 
using namespace std;
int n,num[25],ans = 0;
int check[1005] = {1};

void func(int s,int sum){//从s开始选数字，和为sum
    if(check[sum] == 0){
        check[sum] = 1;
        ans++;
    }
    for(int i = s; i <= n; i++){
        sum += num[i];
        func(i + 1, sum);
        sum -= num[i]; //回溯
    }
}

int main(){
    cin >> n;
    for(int i = 0; i < n; i++){
        cin >> num[i];
    }
    func(0,0); 
    cout << ans;
}

DFS可以解决集合问题

题目描述
​ 有很多人在门口排队，每个人将会被发到一个有效的通行密码作为门票。一个有效的密码由 L 个小写字母组成，至少有一个元音 (a,e,i,o,u)和两个辅音，并且是按字母表顺序出现的，例如 abc 是有效的，而 cba 不是。
​ 现在给定一个期望长度 L 和 C 个小写字母，输出所有有效密码。

输入
​ 第一行两个正整数 L,C。（3≤L≤15,C≤26）
​ 接下来一行输入 C个小写字母。

输出
​ 按照字母表顺序输出所有密码，一行一个，若密码超过 2500025000 时，只输出前 2500025000 个密码。

样例输入
4 6
a t c i s w

样例输出
acis
acit
aciw
acst
acsw
actw
aist
aisw
aitw
astw
cist
cisw
citw
istw

数据规模与约定
​ 时间限制：1 s
内存限制：256 M
​ 100% 的数据保证 3≤L≤15,C≤26

#include 
#include 
using namespace std;
int L,C;
char num[26];
char ans[20];
int cnt = 0;
int fu,yuan,num2;

int func(int s, int left){ //从s开始还剩left个
    if(left == 0){ 
        if(yuan >= 1 && fu >= 2){
            for(int i = 0; i < L; i++){
                cout << ans[i];
            }
        
            cout << endl;
            num2++;
            if(num2 == 25000){
                return -1;
            }
        }
    }
    for(int i = s; i < C; i++){
        ans[cnt++] = num[i];
        int f = 0;
        if(num[i] == 'a' || num[i] == 'e' || num[i] == 'i' || num[i] == 'o' || num[i] == 'u'){ 
            yuan++;
            f = 1;
        }else{
            fu++;
        }
        if(func(i+1,left-1) == -1){
            return -1;
        }
        if(f == 1){ //回溯
            yuan--;
        }else{
            fu--;
        }
        cnt--;
    }
    return 0;
}

int main(){
    cin >> L >> C;
    for(int i = 0; i < C; i++){
        cin >> num[i];
    }
    sort(num,num+C);
    func(0,L);
}

题目描述
​ 读入一个用邻接矩阵存储的无向图，输出它的深度优先遍历序列。（以 1为起点，按照编号越小权值越大的规则）

输入
​ 第一行一个正整数 NN，表示节点个数。（5≤N≤20）
​ 接下来输入一个邻接矩阵，a[i,j]=0表示 i,j之间不存在边，=1 说明存在边。

输出
​ 格式参照样例

样例输入
8
0 1 1 0 0 0 0 0
1 0 0 1 1 0 0 0
1 0 0 0 0 0 1 1
0 1 0 0 0 1 0 0
0 1 0 0 0 1 0 0
0 0 0 1 1 0 0 0
0 0 1 0 0 0 0 1
0 0 1 0 0 0 1 0

样例输出
1-2-4-6-5-3-7-8

#include 
using namespace std;
int n;
int num[25][25],check[25],flag;

void func(int s){
    if(flag == 1){
        cout << '-';
    }    
    flag = 1;
    cout << s;
    for(int i = 1; i <= n; i++){
        if(num[s][i] == 1 && check[i] == 0){
            check[i] = 1;
            func(i);
        }
    }
}

int main(){
    cin >> n;
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n ; j++){
            cin >> num[i][j];
        }
    }
    for(int i = 1; i <= n; i++) {
        if(check[i] == 0){
            check[i] = 1;
            func(i);
        }
    }
    return 0;
}

BFS

广度优先搜索（BFS） 广度优先搜索在进一步遍历图中顶点之前，先访问当前顶点的所有邻接结点。 a .首先选择一个顶点作为起始结点，并将其染成灰色，其余结点为白色。 b. 将起始结点放入队列中。 c. 从队列首部选出一个顶点，并找出所有与之邻接的结点，将找到的邻接结点放入队列尾部，将已访问过结点涂成黑色，没访问过的结点是白色。如果顶点的颜色是灰色，表示已经发现并且放入了队列，如果顶点的颜色是白色，表示还没有发现 d. 按照同样的方法处理队列中的下一个结点。

模板

#include
#include
using namespace std;
#define max_n 500
struct Node{
    int x,y,num;
};
char mmap[max_n + 5][max_n + 5];
queue<Node> q;
  int n,m;
int dir[4][2] = {0,1,0,-1,1,0,-1,0};
int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++){  //从1开始防止越界
        for(int j = 1; j <= m; j++){
            cin >> mmap[i][j];
            if(mmap[i][j] == 's'){
                q.push({i,j,0});
            }   
        }
    }
    while(!q.empty()){
        Node temp = q.front();
        q.pop();
        for(int i = 0; i < 4; i++){
            int x = temp.x + dir[i][0];
            int y = temp.y + dir[i][1];
            //判断是否越界
            /*if(x<=0 || y<= 0|| x>n || y>m){
            	continue;
            }*/
            if(mmap[x][y] == 'g'){ //终点
                cout << temp.num + 1 << endl;
                return 0;
            }
            if(mmap[x][y] == '.'){ //可以通过
                mmap[x][y] = 0;
                q.push({x,y,temp.num+1});
            }
        }

    }
    cout << "No" << endl;
    return 0;
}

题目描述
​ 小明刚刚参加完期中考试，“这次又能得班级第一了”，他沾沾自喜，想起之前一直努力学习的自己，他决定去西城红场看个电影放松一下。现在小明想从学校走到电影院，因为市政大力修路和挖地铁，有些道路不允许步行，请判断小明能否走到电影院（只能朝上下左右四个方向行走），如果能到，则输出最短步数，如果不能到，则输出 No.

输入
​ 第 1 行两个数 n 和 m 表示地图有 n 行 m 列 2≤n,m≤500 第 2 行至第 n+1 行为地图，其中 s 表示学校 g表示电影院​ . 为步行可以通过的点 # 为步行不可通过的点

输出
​ 能走到电影院输出最少步数​ 不能走到电影院输出 No

样例输入
4 4
…s
…##
…
.g…

样例输出
5

数据规模与约定
​ 时间限制：1 s
内存限制：256 M
100% 的数据保证 2≤n,m≤500

#include 
#include 
using namespace std;

char mmap[505][505];
int n,m,sx,sy;
int dir[4][2]={
    0,1,
    1,0,
    -1,0,
    0,-1
};
struct Node{
    int x,y,cnt;
};
queue<Node> que;
int main(){
    cin >> n >> m;
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < m; j++) {
            cin >> mmap[i][j];
            if(mmap[i][j] == 's'){
                Node node;
                node.x= i;
                node.y = j;
                node.cnt = 0;
                que.push(node);
            }
        }
    }
    while(!que.empty()){
        Node temp = que.front();
        que.pop();
        for(int i = 0; i < 4; i++){
            int tx = temp.x + dir[i][0];
            int ty = temp.y + dir[i][1];
            if(tx < 0 || ty < 0 || tx >= n || ty >= m){
                continue;
            }
            if(mmap[tx][ty] == 'g'){
                cout << temp.cnt + 1 << endl;
                return 0;
            }
            if(mmap[tx][ty] == '.'){
                mmap[tx][ty] = 0;
                que.push({tx,ty,temp.cnt + 1});
            }
        }

    }
    cout << "No" << endl;
    return 0;
}

带有条件的广搜

题目描述
​ 小明看完了电影，是时候回家了，可是这时他突然得知小米之家的小米9现货开卖了，这款手机小明已经想了一个多月，知道这个消息后的他十分兴奋，一定要在回家之前先去小米之家买手机（城市中有一个或多个小米之家），请计算小明从电影院到任意一个小米之家买手机后回家的最短距离（只能朝上下左右四个方向行走，除了障碍物外，其他地方都可以通过），数据保证可以买完手机后回家。

输入
​ 第 1 行两个数 n 和 m 表示地图有 n 行 m 列 2≤n,m≤2000​ 第 2 行至第 n+1 行为地图 其中 S 表示电影院 T 表示家 P 表示小米之家​ . 为可以通过的点 # 为障碍物

输出
​ 一个整数 表示小明从电影院去小米之家再回家的总距离

样例输入
5 5
.S…
###…
…T
.P##.
P…

样例输出
11

数据规模与约定
​ 时间限制：5 s
​ 内存限制：256 M
​ 100% 的数据保证 2≤n,m≤2000

#include 
#include 
using namespace std;

struct node {
    int x, y, s, f; //s代表几步，f代表有没有手机
};

int n, m, check[2005][2005];//查重数组，1代表没手机经过，2代表有手机经过，3没有手机和有手机都经过
char mmap[2005][2005];
int dir[4][2] = {0, 1, 1, 0, 0, -1, -1, 0};

int main() {
    queue<node> que;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> mmap[i][j];
            if (mmap[i][j] == 'S') {
                que.push({i, j, 0, 0});
                check[i][j] = 1;
            }
        }
    }
       while (!que.empty()) {
        node temp = que.front();
        que.pop();
        for (int i = 0; i < 4; i++) {
            int x = temp.x + dir[i][0];
            int y = temp.y + dir[i][1];
            if (temp.f == 0 && check[x][y] & 1) continue;//没有手机
            if (temp.f == 1 && check[x][y] & 2) continue;//有手机
            if (temp.f == 1 && mmap[x][y] == 'T') {//有手机到家
                cout << temp.s + 1 << endl;
                return 0;
            }
            if (temp.f==0&& mmap[x][y] == '.' || mmap[x][y] == 'S' || mmap[x][y] == 'T') {//没手机可以经过的路径
                que.push({x, y, temp.s + 1, temp.f});
                check[x][y] +=  1;
            }
            if (temp.f==1&& mmap[x][y] == '.' || mmap[x][y] == 'S' ) {//有手机可以经过的路径
                que.push({x, y, temp.s + 1, temp.f});
                check[x][y] +=  2;
            }
            if (mmap[x][y] == 'P') {
                que.push({x, y, temp.s + 1, 1});
                check[x][y] = 3;
            }
                    }
    }
    return 0;
}

广搜搜索树
559. N叉树的最大深度

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector _children) {
        val = _val;
        children = _children;
    }
};
*/
//广搜
/*class Solution {
public:
    int maxDepth(Node* root) {
        if(!root) return 0;
      queue q;
      q.push(root);
      int deep_max = 0;
      while(!q.empty()){
          deep_max++;
          for(int i = q.size(); i > 0; i--){
               Node * temp = q.front();
               q.pop();
              for(auto a : temp->children){
                  q.push(a);
              }
          }

      }
      return deep_max;   
    }
};*/
//深搜
class Solution {
public:
    int maxDepth(Node* root) {
        if(root == NULL) return 0;
         int deep_max =  0;
         for(auto i : root->children){
            int temp = maxDepth(i);
            deep_max = max(deep_max,temp);
        }
        return deep_max+1;
    }
};

Leetcode 剑指 Offer 32 - II. 从上到下打印二叉树 II

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> v;
    vector<vector<int>> levelOrder(TreeNode* root) {
        if(root == nullptr) return v;
        queue<TreeNode * > q;
        q.push(root);
        vector<int> vec;
        while(!q.empty()){
            for(int i = q.size(); i; i--){
                TreeNode * temp = q.front();
                vec.push_back(temp->val);
                q.pop();
                if(temp->left){
                    q.push(temp->left);
                }
                 if(temp->right){
                    q.push(temp->right);
                }
            }
            v.push_back(vec);
            vec.clear();
        }
        return v;
    }
};