pytorch实现 logistic 回归
第一次尝试用pytorch来搭建一个神经网络,原代码是吴恩达深度学习第一课第二周的作业,没有用到框架。不得不提一下,这个课程作业质量相当高,不仅给出了模型实现的详细思路,还包括一些代码技巧,非常细致,感兴趣的同学可以去看一下。
话不多说,来看实现过程。
logistic回归解决的是二分类问题,我们的任务是给图片分类,判断一张图片是否是猫。
首先,导入各种包。
import numpy as np
import torch
from torch import nn
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset
import torch.utils.data as Data
from torch.nn import init
这里我们导入了h5py包,是用来处理.h5格式的图片的。
导入数据
# Loading the data (cat/non-cat)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
load_dataset()函数是lr_utils包里的,不用自己写。
以下是数据参数。

数据预处理
#将shape变成(209,64×64×3)和(50,64×64×3)
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1)
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1)
# 归一化
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.
# 将numpy转化为torch
train_x = torch.from_numpy(train_set_x).float()#计算loss要float类型
test_x = torch.from_numpy(test_set_x).float()
train_y = torch.from_numpy(train_set_y.T).float()
test_y = torch.from_numpy(test_set_y.T).float()
定义模型
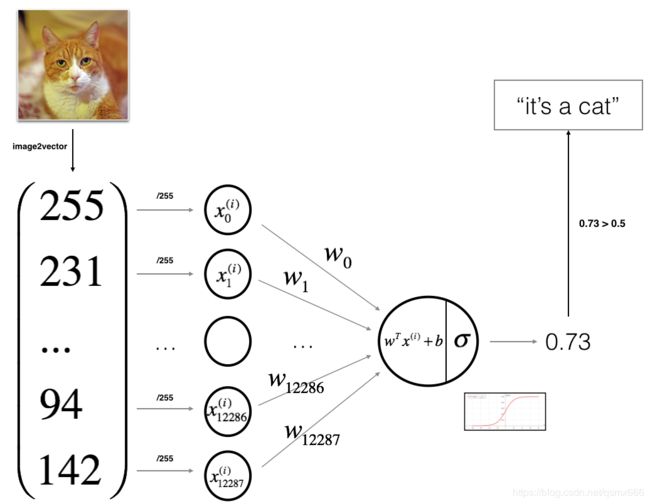
模型思路是将图片转化为一维向量后,输入神经网络,先经过一个线性层转化为单个值,再经过sigmoid层转化为0到1之间的值,如果大于0.5就输出1,表示“这是一只猫”,反之输出0,表示“这不是猫”。
num_inputs=12288
num_outputs=1
class LogisticRegression(nn.Module):
def __init__(self):
super(LogisticRegression, self).__init__()
self.linear = nn.Linear(num_inputs, num_outputs)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.linear(x)
x = self.sigmoid(x)
return x
实例化
net = LogisticRegression()
初始化模型参数
init.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias, val=0)
以上两个函数都来自torch.nn中的init包。weight用的是正态初始化函数,bias初始化为0。
定义损失函数
loss = nn.BCELoss()
BCEloss()是交叉熵损失函数,在pytorch中专门用于二分类。
定义优化函数
optimizer = torch.optim.SGD(net.parameters(), lr=0.005, momentum=0.9)
这里用的是动量法,是梯度下降算法的优化算法。
计算准确率
def evaluate_accuracy(x,y,net):
out = net(x)
correct= (out.ge(0.5) == y).sum().item()
n = y.shape[0]
return correct / n
数据中真实标签是用0和1表示的,而sigmoid层的输出是0到1之间的数(很多个),这里用torch.ge()函数将大于等于0.5的值转化为1,将小于0.5的值转化为0。有个很好玩的事,吴恩达老师在课程中再三强调尽量不要使用for循环,能用向量就用向量,结果在本次作业代码里还是用了hhh,还加了一句“If you wish, you can use an if/else statement in a for loop”。我本来也是用的for循环,后来才发现pytorch有个这么好用的函数。
好了,不扯了,接下来是训练过程。
训练&预测
def train(net,train_x,train_y,test_x,test_y,loss,num_epochs,optimizer=None):
for epoch in range(num_epochs):
out = net(train_x)
l = loss(out, train_y)
optimizer.zero_grad()
l.backward()
optimizer.step()
train_loss = l.item()
if (epoch + 1) % 100 == 0:
train_acc = evaluate_accuracy(train_x,train_y, net)
test_acc = evaluate_accuracy(test_x, test_y, net)
#print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f' %
# (epoch + 1, train_loss, train_acc , test_acc))
print('epoch %d ,loss %.4f'%(epoch + 1,train_loss)+', train acc {:.2f}%, test acc {:.2f}%'
.format(train_acc*100,test_acc*100))
num_epochs=1000
train(net, train_x,train_y,test_x,test_y,loss, num_epochs,optimizer)
简单概括一下训练步骤:
1.前向传播求损失函数。
2.梯度归零。
3.反向传播求梯度。
4.更新参数。
我们将迭代次数设置为1000,每迭代一次参数都会被更新。
结果

以上是训练结果,可以看到训练500次左右训练集上的准确率就到达了100%,而测试集的准确率达到了70%。这个效果其实是不错的,因为我们的模型只是一个简单的线性分类器并且数据集很小。而测试集的准确率小于训练集的原因是过拟合,可以通过丢弃法、权值衰减等方法解决这个问题。还有一点是我注意到每次运行的输出结果是不一样的,测试集的准确率有时在68%,有时会超过70%。出现这种情况是因为模型参数是随机初始化的。训练结果会有一些不同,但会在一个小的范围内变化。
关于学习率
这是吴恩达课程作业中的延伸部分,讨论了不同学习率对模型效果的影响。
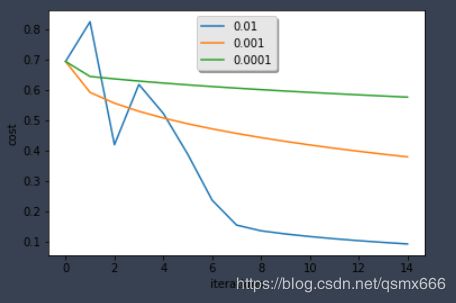
总结:学习率不同,模型损失和预测结果也不相同。损失小并不意味着模型好,因为可能存在过拟合。在搭建神经网络时,我们要注意选取合适的学习率,必要时可以采取一些避免过拟合的方法。
最后的最后,写一下感想。其实代码很简单,就几十行,可是过程中出现各种bug,加上自己磨磨蹭蹭,几乎折腾了一天,最后看到输出,哇,老泪纵横。刚开始感觉神经网络很神奇,就那么几行代码居然能识别图片,现在明白了它其实就是一个复杂化的线性回归(当然不全是线性),我们要做的就是去拟合数据,利用损失函数不断调整参数,这就是一个学习的过程。
