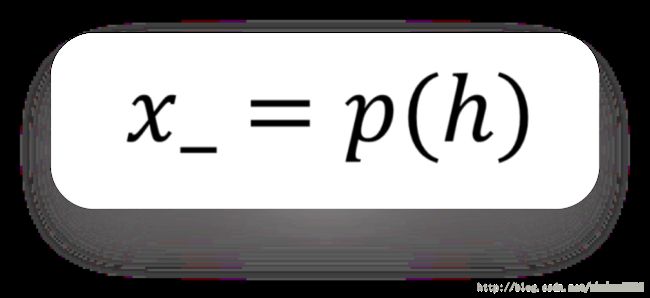对抗自编码器指南之一：自编码器

如果你知道如何编写Tensorflow代码来对MNIST数字进行分类，那么阅读本文就不会有太多障碍，否则我会强烈建议你先阅读Tensorflow网站上的这篇 文章。

我们不再需要任何重大的新突破就可以获得真正的AI!!!???

这是非常离谱、极其可笑的错误观点。 正如我之前所说：人类和动物的学习大部分都是无监督的。 如果把智能比做一个蛋糕，那么无监督（unsupervised）学习才是真正的蛋糕，有监督（supervised）学习只是蛋糕上的糖霜，而强化（reinforcement）学习则是蛋糕上那些作为点缀的樱桃。

现在我们已经知道了如何制作糖霜和樱桃，但是还不知道如何做蛋糕。 在我们可以开始考虑实现真正的AI之前，首先要先解决无监督学习的问题。 而这只是我们实现真正AI的已知的障碍之一。 还有那些我们不知道的事情呢？

这是AlphaGo胜利后Facebook的AI研究主管Yan Lecun的一句话。

我们知道卷积神经网络（CNN）或者全连接网络（也被称为MLP，即多层感知器）可以用来进行图像识别。 但是，单纯使用CNN或MLP并不能胜任所有的任务，例如：分离图像的内容和风格、生成真实的图像（生成式模型）、使用非常少量的标注数据进行分类、执行数据压缩（例如文件压缩）等。

现在要实现上述这些任务，每一个可能都需要专有的网络架构和训练算法。 但是，如果我们能够使用同一种架构来实现上述所有的任务，是不是很酷？对抗自编码器（Adversarial Autoencoder）就是这样一种架构，它可以执行所有这些任务，甚至更多。

在这个系列教程中，我们将利用MNIST数据集来构造这么一个对抗自编码器，它可以对数字（0~9）的图像执行（有损）压缩、自动分离数字图像的风格和内容（来生成不同风格的数字）、利用少量（1000个）标注数据可以获得95％的分类准确度，而且它是一个生成式模型、可以生成以假乱真的数字。

在介绍对抗自编码器的理论和实现之前，让我们先后退一步，从自编码器（Autoencoder）开始，先利用tensorflow实现一个简单的自编码器。

自编码器是一种特殊的神经网络（neural network），它的输出目标（target）就是输入（所以它基本上就是试图将输出重构为输入），由于它不需要任何人工标注，所以可以采用无监督的方式进行训练。

自编码器包括两个组成部分：编码器和解码器。

编码器（Encoder）负责把输入x（可以是图像、单词嵌入向量、视频或音频数据）转换为中间输出h（h的维度通常比x低，即降维）。 例如，编码器可以把100×100大小的图像x转换为100×1（当然可以是任何尺寸）的输出h，h常被称为隐编码（lantent code）。 在这种情况下，编码器只是对图像进行压缩，使其占用较小的空间，正如我们看到的， h 只需要x 百分之一的存储空间（这会导致某些信息丢失，即有损压缩）。

让我们来考虑一下像WinRAR这样的压缩软件（你还在免费试用吗？），它可以用来压缩文件以获得占用更少空间的zip（或rar...）文件。 编码器在自编码器架构中就是执行类似的操作。

如果编码器使用函数q来表示，那么：

解码器（Decoder）接收编码器的输出，并试图在其输出端重构编码器的输入。 在前面编码器的例子中，h的大小是100×1，解码器的目标是将h转换为初始的100×100大小的图像。 我们训练解码器以便从隐编码h中获取尽可能多的信息来重构x 。

因此，解码器的操作与在WinRAR上执行解压缩类似。

如果函数p代表我们的解码器，那么重建图像x_对应于：

维度压缩（dimension reduction）只有在输入中存在某种相关（correlate）时才起作用（如来自同一领域的多个图像）。 如果我们训练自编码器时，每次都传入完全随机的输入，训练就会失败。 最终一个自编码器可以在编码器的输出端产生给定输入的降维输出，这非常类似于主成分分析（ PCA: Primary Component Analysis ）。 而且由于我们在训练过程中并不需要使用任何人工标注，所以它也是一个无监督模型。

但是，除了降维以外，自编码器还有什么用？

• 图像去噪：输入有噪声的图像，输出清晰的无噪声图像。下图是手写数字去噪自编码器的例子：
  
• 语义散列技术通过降维使信息检索更快（我发现这非常有趣！）。
• 以对抗方式训练出的自编码器可以用作生成式（generative）模型，这一点我们将在后面进一步深入。

我把这篇文章分成四个部分：

• 第1部分：自编码器

我们将从一个简单自编码器的Tensorflow实现开始，使用它来压缩MNIST（你肯定听说过这个数据集）图像的维度。

• 第2部分：探索对抗自编码器的隐空间

我们将使用对抗学习手段，在隐编码（编码器的输出）上引入约束条件。

• 第3部分：分离样式与内容

在这里，我们将以相同的写作风格生成不同的样本图像。

• 第4部分：用1000个标签分类MNIST数据。

我们将训练一个自编码器来对MNIST数字进行分类，只用1000个标注过的输入来获得大约95％的准确度（令人印象深刻，对吧？）。

现在进入第一部分，我们先看看需要实现的网络结构， 。

如前所述，自编码器（AE）包括一个编码器和一个解码器，让我们从一个简单的全连接编码器架构开始：

输入层有784个神经元（将图像拉平到单一维度），两个隐层分别包含1000个使用relu激活函数的神经元，输出层使用2个神经元，都不使用激活函数以便获得隐编码。

如果你想直接试试代码，可以查看这个链接。

为了在Tensorflow中实现上述架构，我们将从一个dense()函数开始，它将基于给定的样本输入x、输入神经元数量n1和输出神经元数量n2，自动创建一个全连接层。 name参数用于设置变量域（variable_scope）的名称。 关于共享变量和变量域的更多内容可以查看这里（我强烈建议你看一下）：

def dense(x, n1, n2, name):
    """
    Used to create a dense layer.
    :param x: input tensor to the dense layer
    :param n1: no. of input neurons
    :param n2: no. of output neurons
    :param name: name of the entire dense layer.i.e, variable scope name.
    :return: tensor with shape [batch_size, n2]
    """
    with tf.variable_scope(name, reuse=None):
        weights = tf.get_variable("weights", shape=[n1, n2],
                                  initializer=tf.random_normal_initializer(mean=0., stddev=0.01))
        bias = tf.get_variable("bias", shape=[n2], initializer=tf.constant_initializer(0.0))
        out = tf.add(tf.matmul(x, weights), bias, name='matmul')
return out

我使用了tf.get_variable()而不是tf.Variable()来创建权重和偏差变量，以便后续可以在训练好的模型（编码器或解码器）尝试不同的变量并查看其输出。

接下来，我们将使用这个dense()函数来实现编码器体系结构。 代码很简单，但请注意，我们没有在编码器的输出中使用任何激活函数：

def encoder(x, reuse=False):
    """
    Encode part of the autoencoder
    :param x: input to the autoencoder
    :param reuse: True -> Reuse the encoder variables, False -> Create or search of variables before creating
    :return: tensor which is the hidden latent variable of the autoencoder.
    """
    if reuse:
        tf.get_variable_scope().reuse_variables()
    with tf.name_scope('Encoder'):
        e_dense_1 = tf.nn.relu(dense(x, input_dim, n_l1, 'e_dense_1'))
        e_dense_2 = tf.nn.relu(dense(e_dense_1, n_l1, n_l2, 'e_dense_2'))
        latent_variable = dense(e_dense_2, n_l2, z_dim, 'e_latent_variable')
return latent_variable

• reuse标志用于重用训练好的编码器。
• input_dim = 784, n_l1 = 1000, n_l2 = 1000, z_dim = 2 。

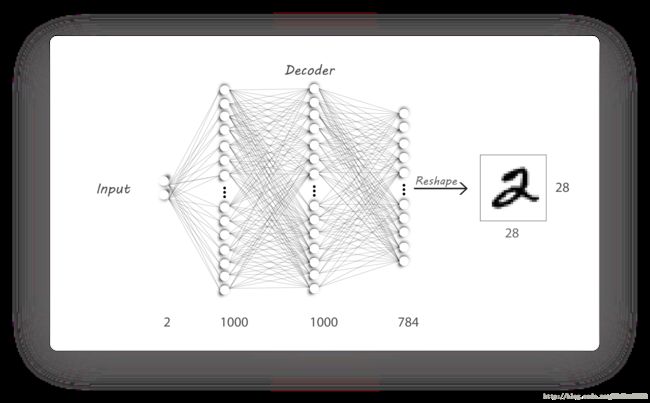
解码器是以类似的方式实现的，我们期望的架构如下：

再次使用dense()函数来构建我们的解码器。 不过这里我在输出层使用了sigmoid激活函数，以确保输出值介于0和1之间（与输入的值范围相同）。

• z_dim = 2, n_l2 = 1000, n_l1 = 1000, input_dim = 784，与编码器相同。

使用编码器的输出作为解码器的输入：

encoder_output = encoder(x_input)
decoder_output = decoder(encoder_output)

现在已经实现了前面示意图中描述的自编码器架构。 我们将利用占位符x_input （size：batch_size，784）提供输入，将target（目标）设置为与x_input（输入）相同， 然后对x_input（输入）与decoder_output（重构的输入）进行比较 。

所使用的损失函数是均方误差（MSE:Mean Squared Error），它找出输入（ x_input）和输出图像（ decoder_output）中像素之间的距离。 我们称之为重构损失（reconstruction loss），因为我们的主要目标就是重构输入。

上面的公式用来计算输入和输出（重构的输入）的平方差。 在Tensorflow中实现这个计算很容易：

loss = tf.reduce_mean(tf.square(x_target - decoder_output))

我使用的优化器是AdamOptimizer（你可以随意试试新的优化器，我还没有尝试过其他的），学习率为0.01，beta1为0.9。 在Tensorflow中预置了AdamOptimizer的实现，你可以直接拿来使用：

optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate, beta1=beta1).minimize(loss)

请注意，我们使用同一个损失函数让误差反向传播过编码器和解码器。

最后，我们加载MNIST图像集，使用100大小的批次来训练我们的模型，每个批次的100张图像同时也作为网络要学习的输出目标。

step = 0
with tf.Session() as sess:
    sess.run(init)
    if train_model:
        tensorboard_path, saved_model_path, log_path = form_results()
        writer = tf.summary.FileWriter(logdir=tensorboard_path, graph=sess.graph)
        for i in range(n_epochs):
            n_batches = int(mnist.train.num_examples / batch_size)
            for b in range(n_batches):
                batch_x, _ = mnist.train.next_batch(batch_size)
                sess.run(optimizer, feed_dict={x_input: batch_x, x_target: batch_x})
                if b % 50 == 0:
                    batch_loss, summary = sess.run([loss, summary_op], feed_dict={x_input: batch_x, x_target: batch_x})
                    writer.add_summary(summary, global_step=step)
                    print("Loss: {}".format(batch_loss))
                    print("Epoch: {}, iteration: {}".format(i, b))
                    with open(log_path + '/log.txt', 'a') as log:
                        log.write("Epoch: {}, iteration: {}\n".format(i, b))
                        log.write("Loss: {}\n".format(batch_loss))
                step += 1
            saver.save(sess, save_path=saved_model_path, global_step=step)
    else:
        all_results = os.listdir(results_path)
        all_results.sort()
        saver.restore(sess,
                      save_path=tf.train.latest_checkpoint(results_path + '/' + all_results[-1] + '/Saved_models/'))
generate_image_grid(sess, op=decoder_image)

完整的代码都放到github上了。

注意事项

• generate_image_grid()函数将一组数字输入给训练好的解码器来生成一组图像，这也是get_variable派上用场的地方。
• 每次运行代码都将在下面目录生成所需的tensorboard文件：

/Results/<model>/<time_stamp_and_parameters>/Tensorboard

• 训练日志文件为：

./Results///log/log.txt

• 将train标志设置为True来训练模型，将其设置为False则显示某个随机输入的解码器输出。

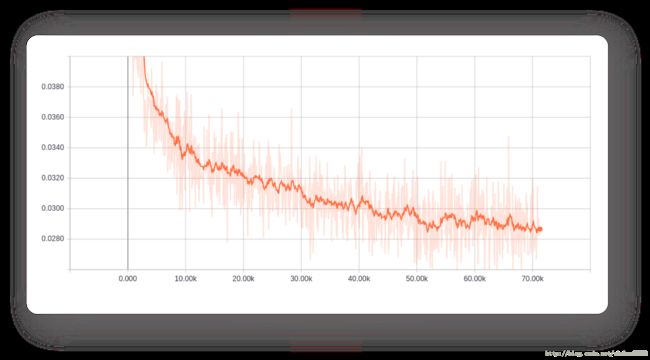
下面是200个周期（eopch）的训练过程中，网络重构损失（reconstruction loss）的变化曲线：

重构损失在逐步减少，这正是我们想要的。

训练过程中重构图像的变化：

注意解码器是如何通过消除输入数字3上面的小的不规则性来实现泛化的。

现在，如果我们向训练好的解码器输入一些随机数（因为隐编码是二维的，所以我输入了0，0），我们会得到一个对应的数字图像吗？

但是上面的图看起来还不是一个清晰的数字（至少对我来说是这样）。

原因在于，编码器的输出不能覆盖整个二维的隐空间（它的输出分布中有很多空白区域）。 因此，如果我们输入了编码器在训练过程中没有生成过的值，可能就会看到解码器输出奇怪的图像。 要解决这个问题，我们可以在产生隐编码时，将编码器的输出限制为具有指定的随机分布（比如一个具有0.0均值和2.0标准偏差的正态分布）。 这正是对抗自编码器所能做到的，我们将在第二部分学习它。

原文：A wizard’s guide to Adversarial Autoencoders: Part 1, Autoencoder?